Introduction
Le titre est curieux n’est-il pas ? en général on fait sonner les cloches comme le président américain Barack Obama lors d’une visite en Birmanie en novembre 2012...

Ceci dit nos flèches peuvent être assimilées à des barres flexibles et donc se mettent à osciller dès qu’on les choque telle une cloche. Le truc rigolo est que le son qui en ressort est tout à fait audible ! Voici un exemple (cliquez pour faire démarrer la lecture du MP3)
En fait le son perçu et la réponse impulsionnelle de la flèche et il est le mélange de beaucoup de fréquences (notes), tout comme une corde de piano ou violon. On parle de fréquence principale et d’harmoniques et en plus on a un bruit de fond coloré (pas uniforme en fréquences). J’ai déjà abordé ce type de problématique fréquentielle lors des articles sur l’emploi de masselottes sur la corde (voir Oscillations de la corde (Partie I) pour le premier de la liste).
Ce n’est pas pour faire une symphonie que je vais faire cette article !
Il se trouve que les fréquences (notes) d’une flèche sont directement reliées à sa rigidité (produit du module d’Young $E$ et du moment d’inertie $I$ rencontrés lors de l’article Le spine (statique) d’une flèche) et sa masse par unité de longueur $\mu$ et la longueur elle-même $L$ :
$$ \nu \propto \frac{1}{L^2} \sqrt{\frac{E I}{\mu}} \quad\quad Eq.1 $$
Or, l’étude de la déformation de la flèche soumise à la pression exercée par la corde sur l’encoche lors de la phase de propulsion (notion de spine dynamique) est régie par une équation différentielle du type que je détaillerai lors d’un prochain article :
$$ \mu \frac{\partial^2 y(x,t)}{\partial t^2} = - E I \frac{\partial^4 y(x,t)}{\partial x^4} + \frac{\partial}{\partial x} \left[ H(x,t) \frac{\partial y(x,t)}{\partial x}\right] $$
avec $y(x,t)$ le déplacement latéral de la flèche en un point $x$ à un instant $t$, et $H(x,t)$ la force résultante de la pression due à l’accélération de l’encoche et qui tient compte des répartition de masse le long de la flèche. Si la résolution de cette équation est bien en dehors de la portée de cet article, on remarque que le rapport $EI/\mu$ entre en ligne de compte et donc fait intervenir les "notes" de la flèche !
Setup et matériels divers
Pour enregistrer les vibrations sonores des flèches étudiées dans cette étude, j’ai utilisé :
- un micro Denon qui sert à configurer les balances des différents baffles d’un Home Cinéma du subwoofer (caisson de basse) jusqu’aux aigüs.
- une carte de numérisation externe de chez Creative : Sound Blaster X-Fi 5.1 USB qui permet de prendre par exemple des trames de son, de les numériser sur 24bits avec un taux de numérisation 96kHz. En pratique j’ai numérisé à 8kHz des trames de 2048 échantillons sur 16bits pour obtenir de bons résultats pour des fréquences jusqu‘à 4kHz bien suffisant dans notre cas.
- Audacity 2.0.3 un programme libre et gratuit pour l’enregistrement et l’édition de son. Il permet de faire l’acquisition du flux des échantillons numérisés par la carte audio via le bus USB, d’en visualiser le déroulement temporel et fréquentiel pour faire des diagnostiques rapides, et de faire des sauvegardes des échantillons numérisés pour un post-processing au format WAV par exemple.
- Mathematica 9 qui me sert pour le traitement du signal : sélection des échantillons, analyse de Fourier pour obtenir les spectres fréquentiels du signal et du bruit ambiant… Ce logiciel est payant bien que les étudiants peuvent bénéficier d’offre préférentielle. Pour une analyse rapide Audacity suffit.
Ensuite pour enregistrer des vibrations autant éviter de les atténuer ! La flèche doit être libre de mouvement [1], je l’ai donc suspendue comme ceci :
Sur la vue de droite on voit le micro en face de la flèche, la carte d’acquisition numérique à droite du PC portable.
Enfin, pour faire « sonner » la flèche il faut se munir d’un instrument pour la frapper sans que ses propres modes de vibrations viennent gêner la mesure : j’ai opté pour un maillet de carreleur avec un embout en caoutchouc.
Mesure des fréquences de diverses configurations : démarche et reproductibilité
Pour cette série de tests, j’ai utilisé des Easton ACE 670 de longueur de tube de 67.5cm (26.6 in) alourdies avec des pointes de 120 grains.
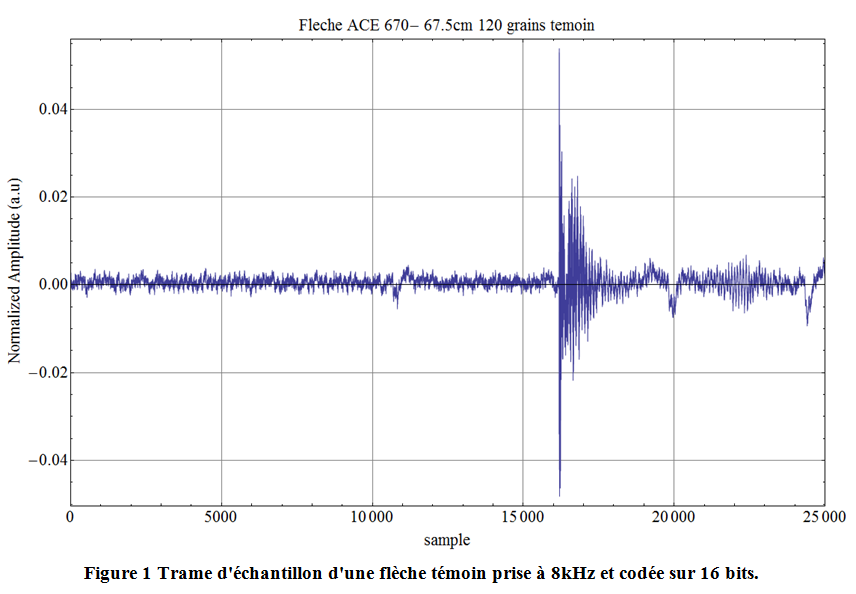
Pour ce premier test, je vais décrire en détail la démarche qui a été utilisée tout au long des prises de mesures et du traitement. Prenons donc une ACE 670 de 67.5cm, je la suspends en face du microphone, je lance l’acquisition (8kHz, 16bits) durant environ 3 à 5 secondes. Ci-dessous un exemple d’acquisition durant 3.125sec à 8kHz soit 25000 échantillons. Audacity ajuste l’échelle pour tenir dans +/- 1 unité arbitraire, comme on n’est pas intéressé par le niveau sonore qui dépend de la force avec laquelle on frappe la flèche, ce n’est pas gênant.
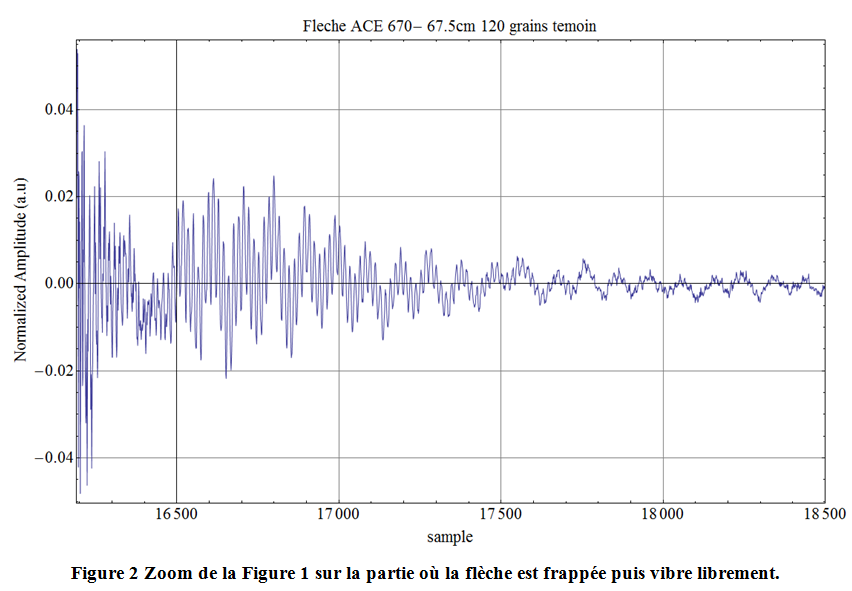
Sur cette Figure 1 on note clairement une première phase d’enregistrement de bruit jusqu’à l’échantillon 16000 environ, puis ensuite la phase où la flèche premièrement a été frappée et ensuite vibre à ses fréquences propres. On peut d’ailleurs zoomer sur partie de vibration de la flèche.
On aperçoit très clairement les oscillations avec plusieurs fréquences de battement : c’est très joli, non ?
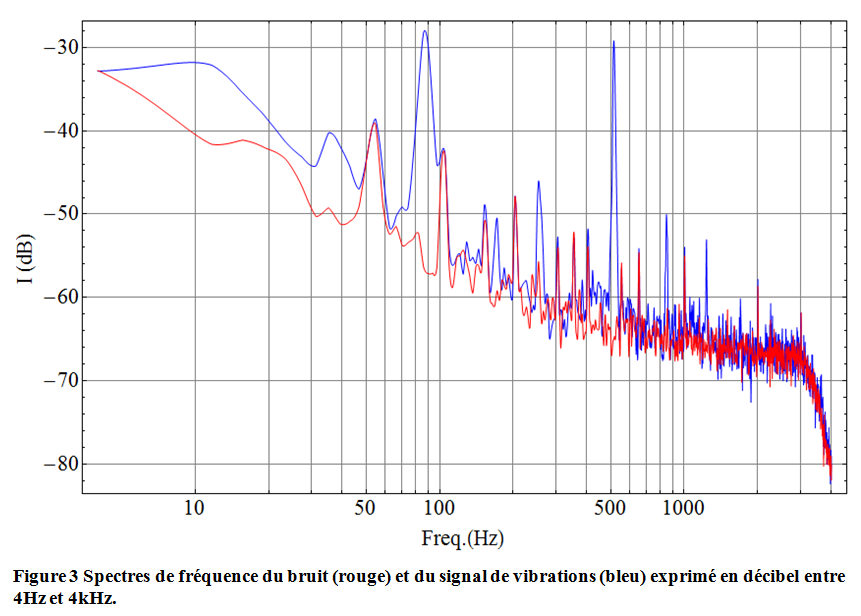
Maintenant que nous avons identifié les deux périodes (« bruit », « signal ») correspondant au bruit de fond ambiant et au signal de vibrations libres de la flèche, on procède à une analyse en fréquence dites de Fourier (FFT : Fast Fourier Transform) du nom du mathématicien français Jean Baptiste Joseph Fourier (1768-1830). Chaque analyse donne comme résultat un spectre : c’est-à-dire une collection de couples (fréquence, intensité). Ci-dessous en bleu le spectre du signal de vibration, en rouge le spectre du bruit de fond.
L’unité des intensités est le dB pour décibel dont la définition est $1dB = 10 Log_{10}(P)$ avec $P$ une puissance proportionnelle à la puissance sonore [2]. Si la puissance est multipliée par 2 alors on ajoute 3dB, et si la puissance est divisée par 2 alors on retranche 3dB. De même le log en base 10 utilisé, montre que passer de -30dB à -40dB revient à diviser par 10 la puissance sonore. On note l’intérêt de mesurer le bruit de fond ET le signal dans le même temps car ainsi on peut travailler en valeur relative et ne pas s’attacher à une calibration absolue de la puissance sonore, ce qui pourrait être fait en chambre sourde et un sonomètre calibré, mais ceci est pour un autre budget et nous n’en avons pas besoin pour mettre en évidence les fréquences propres de la flèche.
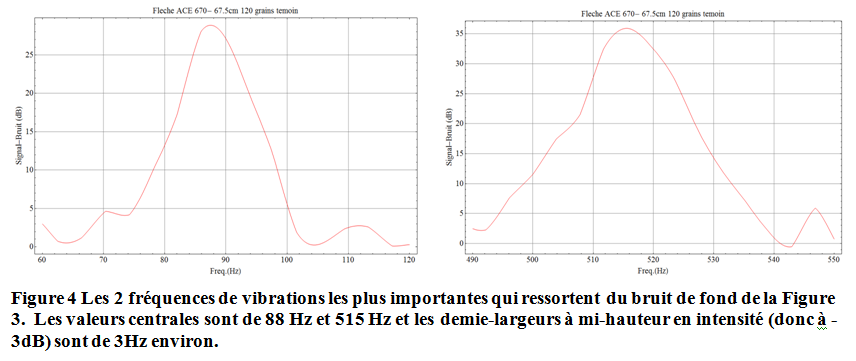
Bon, donc la Figure 3 montre clairement la présence de 2 fréquences particulièrement dominantes dans le spectre de vibrations (bleu) qui ressortent parfaitement du bruit de fond (Figure 4). Les valeurs de ces deux fréquences sont de 88 Hz et 515Hz avec des extensions que l’ont peut quantifier en donnant la demie-largeur de la courbe à mi-hauteur en intensité (on trouve la largeur en prenant l’intercepte avec une ordonnée égale à la valeur maximale – 3dB) : dans les deux cas la demie-largeur est de 3Hz environ. Ainsi, on peut dire qu’on à mesurer les fréquences : $88 \pm 3$ Hz et $515 \pm 3$ Hz
On peut se demander légitimement si d’une flèche à une autre les mesures varient, ou en d’autres termes ces mesures sont-elles fiables ?
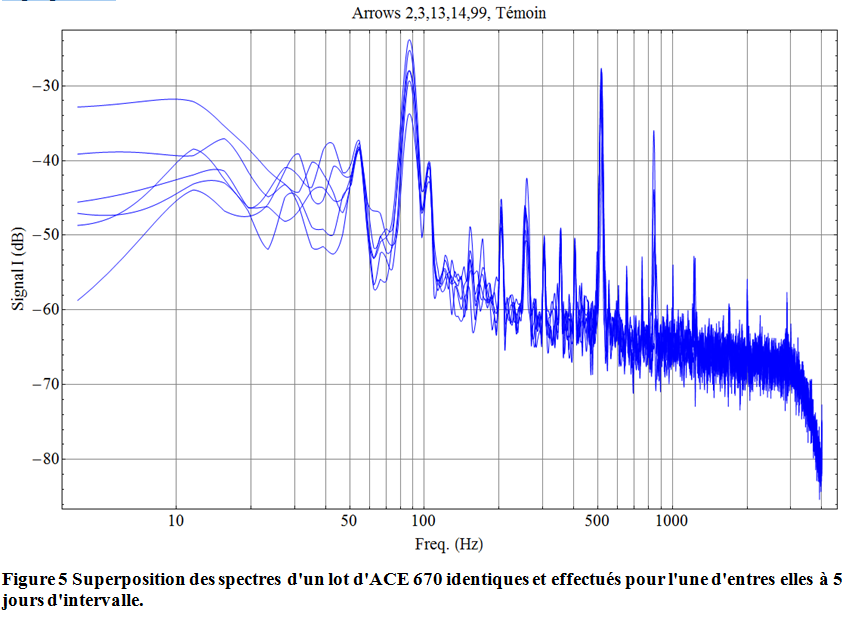
J’ai donc répété la mesure à 5 jours d’intervalle sur la même flèche « témoin » afin de valider le setup, et j’ai aussi pris un lot de flèches « identiques ». Voici les spectres de signal superposés.
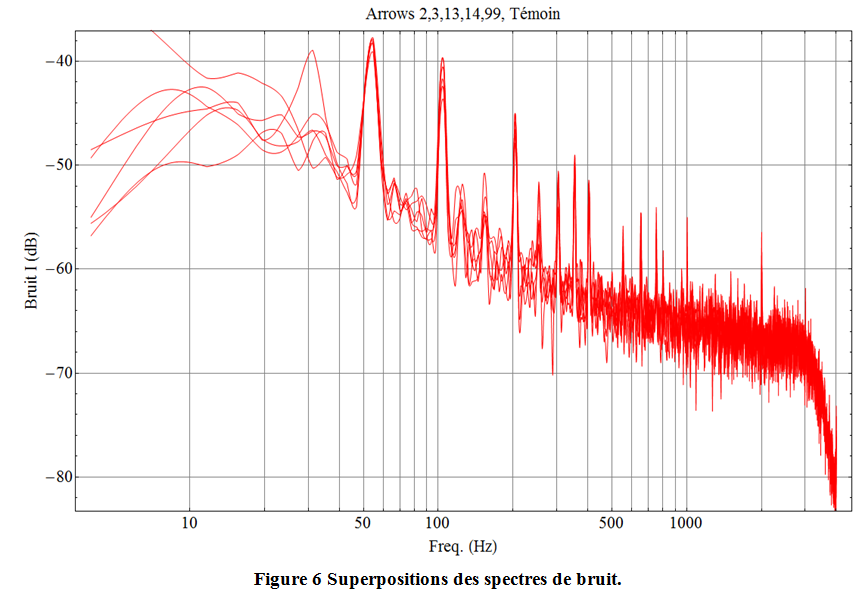
Si l’intensité des raies varient cela est du comme déjà dit à la procédure pour frapper les flèches et au mode d’acquisition par Audacity, par contre la position des raies est bien reproductible, c’est que l’on veut. Le constat est le même pour les spectres de bruit.
Résumé & perspectives
Dans cet article, j’ai attiré votre ’attention sur le fait que nos flèches produisent des vibrations dont certaines sont dans le domaines audibles. De ce constat, j’ai mis au point une procédure de mesure systématique et une première série de tests a permis de conclure que la procédure est fiable. On va donc pouvoir aller plus avant pour observer des variations de fréquences selon la longueur, la rigidité et autres paramètres…
A suivre.

































Commentaires Forum fermé