Introduction
Lors des contrôles de matériel il se peut que vous ayez à vous confronter au problème de mesurer la puissance de votre arc. Elle ne doit pas dépasser la valeur de 60 lbs (tolérance de 1 lbs) d’après le guide des juges de la World Archery consultable en ligne ici.
Je passe sur l’équivalence (abus de langage) entre valeur de masse et puissance d’arc, pour cela je renvoie le lecteur à l’article Unités US et Internationales et je doute que l’arbitre sera à l’écoute de vos explications. Donc, pour le test jusqu’à présent l’arbitre vous tend un peson et vous devez vous exécuter ;) Mais quelques esprits taquins aimeraient suspendre une masselotte de 60 lbs pour s’affranchir des défauts des pesons couramment utilisés. Bon, alors qui dit suspendre une masselotte dit gravité pour mesurer une force.... La gravité est-elle constante sur Terre ???
Comment varie la gravité sur Terre ?
Il se trouve que la gravité moyenne sur Terre $ g_{moy} = 9.81 \mathrm{m/s}^2 $, n’est comme son nom l’indique qu’une moyenne ! Donc on peut se poser la question des variations de celle-ci. Il serait trop long de faire l’historique des mesures de la gravité cependant on peut résumer les corrections (les plus grosses) à apporter à cette valeur standard que tout écolier connait (ou devrait connaître ;) ).
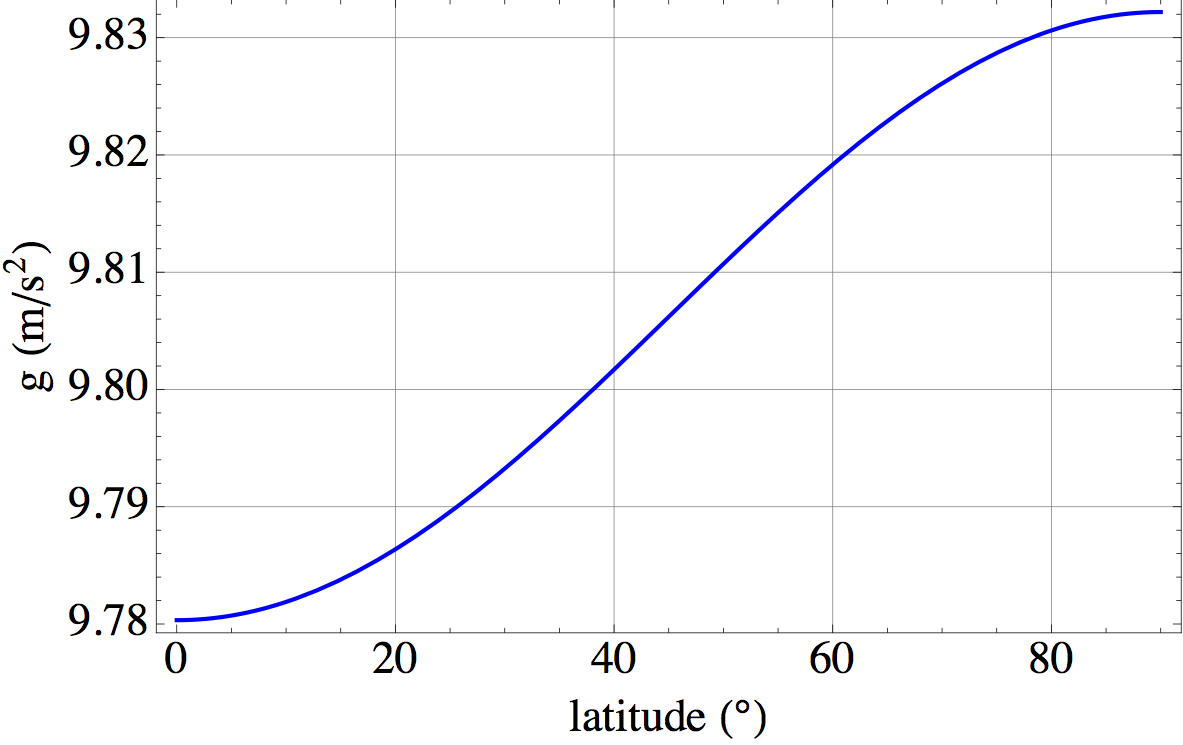
1. La première correction vient de ce que la Terre n’est pas sphérique, plus aplatie aux pôles qu’à l’équateur (la question fut régler par les français sous Louis XIV, de ce temps la les gouvernants avaient confiance dans ces élites...no comment). Bon, cet aplatissement est du à la rotation de la Terre (Newton et Huygens) qui tend par la force centrifuge à faire déplacer les masses d’autant plus quelles sont éloignées de l’axe de rotation donc vient contrebalancer l’attraction vers le centre de la Terre, et que la Terre n’est pas un solide mais plutôt une grosse patate de pâte à modeler. La correction prend la forme suivante
$$ g = 9.7803267714\left( \frac{1+ 0.00193185138639 \sin^2\lambda} {\sqrt{1 - 0.00669437999013 \sin^2\lambda} } \right) $$
où $\lambda$ est la latitude du lieu. La Terre est prise comme un oblate symétrique de révolution Nord-Sud, donc la correction est la même pour
les deux hémisphères et indépendante de la longitude. La figure ci-dessous donne l’allure de la correction en partant de l’équateur (0°) vers les pôles (90°). Donc l’amplitude de la correction est de $ {\bf \pm 0.03} \mathrm{m/s}^2 $ (soit une correction de 3 pour mille).
2. En un lieu géographique donné on peut se trouver plus (en général) ou moins au-dessus du niveau de la mer pour laquelle la valeur standard est calculée. Plus haut de 1 km la gravité se réduit de ${\bf \pm 0.0001} \mathrm{m/s}^2$..
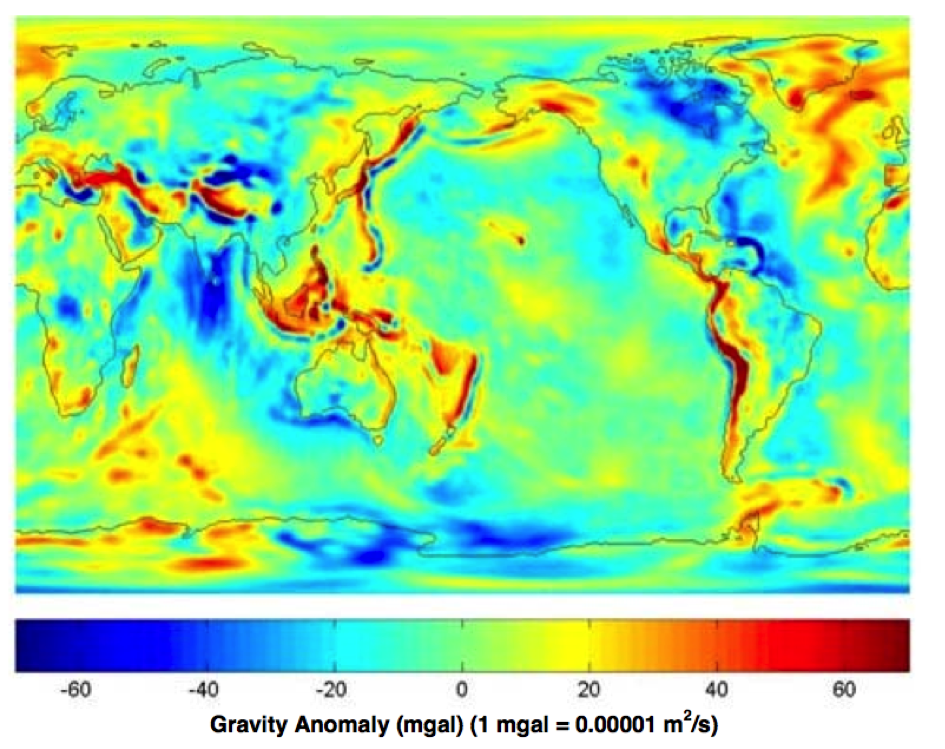
3. L’attraction gravitationnelle est fonction de la masse de l’objet qui attire la pomme de Newton (of course). Or la répartition de la masse à la surface de Terre n’est pas uniforme. La mesure la plus précise de ce phénomène vient de l’espace avec des satellites qui volent en formation (voir la mission GRACE de la NASA. La figure suivante donne la cartographie des differences de gravité par rapport à la valeur locale corrigée des autres effets mentionnés. Il ressort que les variations locale de gravité sont de l’ordre de ${\bf \pm 0.0006} \mathrm{m/s}^2$.
4. Enfin la Terre n’est pas seule dans le Ciel, en particulier le Soleil et la Lune qui génèrent les marées contribuent donc la variation de la gravité avec un effet de ${\bf \pm 0.000003} \mathrm{m/s}^2$..
Finalement selon le type d’usage la précision requise sur la valeur de $g$ demande des connaissances de plus en plus fine et l’on peut illustrer les ordres de grandeurs des effets mentionnés ci-dessus selon le schéma suivant :
Pour notre besoin de peser l’arc ?
Il est clair qu’une expérience de physique qui teste la relativité générale ou la présence d’une 5eme force fondamentale voire même la présence de dimensions cachées de l’espace-temps, ne va pas nécessiter la même précision que la mesure de la puissance d’un arc (ouf ! encore heureux…). Pour nous il faut faire en sorte que les défauts de l’approximation $g \approx 9.81XYZ} \mathrm{m/s}^2$ soient négligeables. C’est à dire qu’il faut savoir jusqu’à quelle décimale on doit connaître $g$ pour que l’on ne se trompe pas ! Or, l’erreur requise pour la qualification d’un arc est de 1 lb sur 60 lbs, soit une précision relative de 1.7%. Si on traduit cela en termes de précision sur la connaissance de la valeur de $g$ locale alors
$$ P = m_{60}\ g \Rightarrow \frac{\Delta P}{P} = \pm 1.7\% = \frac{\Delta g}{g} \Rightarrow \Delta g = \pm 0.17 \mathrm{m/s}^2 $$
[vert]Donc fixer $g = 9.81 \mathrm{m/s}^2$ suffit car l’erreur sur la latitude engendre une erreur sur $g$ bien inférieure. Typiquement cela engendre une erreur de $\pm 0.17$ lbs (ouf ! nous sommes sauvés).
[/vert]
Résumé conclusion
Le test de la puissance de l’arc par l’action d’une masse de 60 lbs dépend de l’intensité de l’attraction gravitationnelle en toute rigueur. Mais après avoir passé en revue les quelques contributions à la non uniformité de la valeur de $g$ dont l’effet principal et l’aplatissement de la Terre aux pôles, on peut se satisfaire de la valeur bien connue de 9.81 $\mathrm{m/s}^2$.