Introduction
Nous allons nous intéresser dans une série d’articles à la phase de vol de la flèche faisant suite à la phase de propulsion traitée dans l’article Dynamique (simple) d’une fléche en phase de propulsion. Le but est de pouvoir comprendre ce qui détermine la réussite du tir et en premier lieu le réglage vertical de son viseur. On se limitera en effet à un mouvement dans un plan vertical (x,y) en négligeant le mouvement latéral. La flèche est considérée comme un objet ponctuel (en fait on s’attache au mouvement de son centre de gravité).
Dans cet article nous allons déterminer la balistique de la flèche en négligeant les frottements dus à l’air.
Les conventions
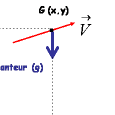
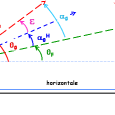
Nous allons déterminer la trajectoire de la flèche après quelle soit sortie de sa phase de propulsion avec une vitesse $\vec{V}_0$ . Pour cela il nous faut un système de repérage des positions (et des angles). La figure suivante fixe les conventions que nous utilisons dans ces articles [1].
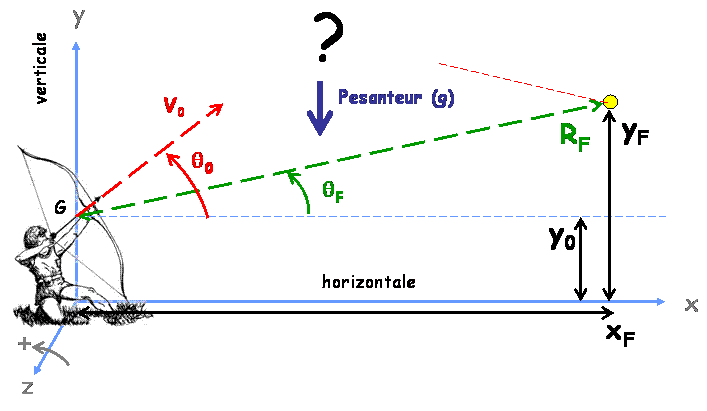
Le repère est positionné de telle façon que les coordonnées du centre de gravité [2] juste après la décoche sont en coordonnées cartésiennes : $x_0 = 0$, $y_0$ et $z_0 = 0$. De même la vitesse initiale de la flèche est repérée dans le même type de repère et a pour coordonnées : $V_{0x} = v_0 \cos\theta_0$, $V_{0y} = v_0 \sin\theta_0$ et $V_{0z} = 0$. Nous avons introduit l’angle $\theta_0$ qui repère la direction initiale de la flèche par rapport à l’horizontale (traits tirés [bleu clair]bleus[/bleu clair]).
L’archer positionné de la sorte tente d’atteindre un objectif matérialisé sur le schéma par le petit disque jaune. On repère ce dernier de deux façons identiques sachant que $Z_F = 0$ :
- en coordonnées dites cartésiennes par le couple ($X_F$, $Y_F$),
- ou en coordonnées dites polaires par le couple ($R_F>0$, $\theta_F$).
On passe facilement d’une représentation à l’autre par les relations [3] :
$$ \begin{align*} X_F & = R_F \cos\theta_F \\ Y_F & = R_F \sin\theta_F \end{align*} $$
Le but du jeu est de déterminer l‘angle $\theta_0$ pour que l’archer puisse atteindre son but. Pour cela il nous faut découvrir ce qu’il se cache derrière le ?. Donc, décochons !!!
Que la pesanteur soit…
Nous avons rencontré dans l’article Dynamique (simple) d’une fléche en phase de propulsion, le principe dit fondamental de la mécanique classique qui stipule que le centre de gravité soumis à une force $\vec{F}$ voit sa quantité de mouvement $\vec{p} = m \vec{V}$ changé d’une quantité $\vec{p}(t_0+dt)-\vec{p}(t_0)$ durant un temps infinitésimal entre $t_0$ et $t_0+dt$ de telle façon que [4] :
$$ \frac{\vec{p}(t_0+dt)-\vec{p}(t_0)}{dt} = \vec{F(t_0)} $$
Or, en l’absence de tout frottement (cf. résistance de l’air même calme, ou courant d’air) la seule force en présence est le poids de la flèche dirigé verticalement vers le bas et d’intensité constante $m g$ ($g = 9,81 \mathrm{m/}\mathrm{s}^2$, cf. Unités US et Internationales) . Comme la masse $m$ de la flèche ne change pas au cours du temps, la variation de la quantité de mouvement se ramène à la variation de la vitesse (multipliée par la masse constante). Ainsi :
$$ m \frac{\vec{V}(t_0+dt)-\vec{V}(t_0)}{dt} = m \vec{g} $$
soit en simplifiant par la masse [5]
$$ \boxed{ \frac{\vec{V}(t_0+dt)-\vec{V}(t_0)}{dt} = \vec{g} } \quad\quad\quad\quad (1) $$
Ainsi, la balistique de la flèche ne dépend pas de sa masse m (à vitesse d’éjection fixée) !.
Le système d’équations couplées
La formule (1) peut être projetée sur les 3 axes du repère cartésien
(Repère des positions et des angles) :
$$ \begin{align*} \left[\vec{V}_x(t_0+dt)-\vec{V}_x(t_0)\right]/dt & = 0\\ \left[\vec{V}_y(t_0+dt)-\vec{V}_y(t_0)\right]/dt & = -g \quad\quad\quad\quad (2) \\ \left[\vec{V}_z(t_0+dt)-\vec{V}_z(t_0)\right]/dt & = 0 \end{align*} $$
La vitesse par exemple $V_x(t_1)$ est par définition la variation
temporelle de la coordonnée $X(t)$ du centre de gravité durant
l’intervalle de temps $t_1$ et $t_1+dt$, c’est-à-dire que d’une
manière générale :
$$ V_x(t_1) = \frac{X(t_1+dt) - X(t_1)}{dt} $$
Et idem pour $V_y(t_1)$ et $V_z(t_1)$ avec $t_1$ qui peut prendre les valeurs $t_0$ ou $t_0+dt$ par exemple. Donc, par exemple le membre de gauche de la première égalité de (2) se traduit en terme de variations de la variable $X(t)$ par
$$ \frac{V_x(t_0+dt)-V_x(t_0)}{dt} = \frac{X(t_0+2dt)-2X(t_0+dt)+X(t_0)}{(dt)^2} \quad\quad\quad\quad (3) $$
Si maintenant au tour de l’instant $t\approx t_0$ on écrit une approximation de l’évolution de $X(t)$ suivante [6] :
$$ X(t) = X(t_0) + (t-t_0) \dot{X}(t_0) + \frac{1}{2}(t-t_0)^2 \ddot{X}(t_0) + \dotsb \quad\quad\quad\quad (4) $$
avec dans les points de suspensions des termes proportionnels
à $(t-t_0)^3$ que l’on néglige, ceci se traduit par le schéma d’évolution temporelle de $X(t)$ suivant
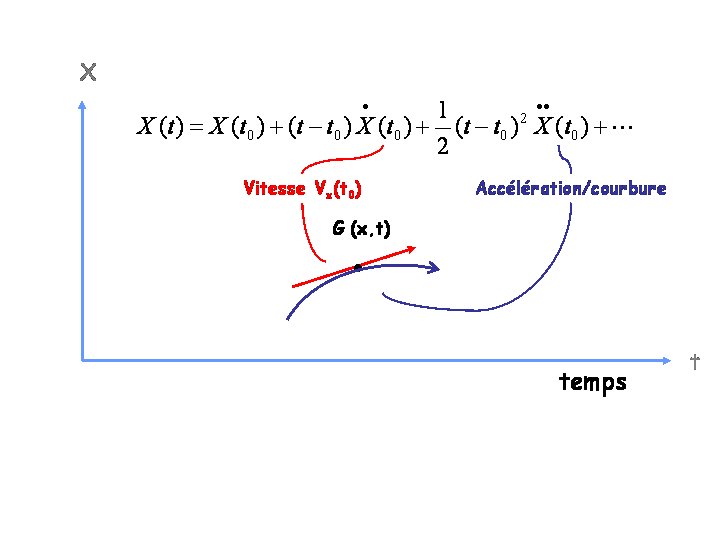
qui permet d’identifier $\dot{X}(t_0)$ à la vitesse instantanée en $t=t_0$ (flèche rouge) qui est tangente à la courbe bleue laquelle présente une courbure vers le bas (concavité) liée à l’accélération (ou décélération ici) dont le coefficient d’intensité en $t=t_0$ est donné par $\ddot{X}(t_0)$ .
On peut appliquer (4) avec les valeurs de $t=t_0+dt$ et
$t=t_0+2dt$, ainsi
$$ \begin{align*} X(t_0+dt ) &= X(t_0) + dt \dot{X}(t_0) + \frac{1}{2}(dt)^2 \ddot{X}(t_0) \\ X(t_0+2dt ) &= X(t_0) + 2dt \dot{X}(t_0) + \frac{1}{2}(2 dt)^2 \ddot{X}(t_0) \end{align*} $$
En reportant ces développements dans le membre de droite de l’égalité (3), nombre de termes s’en vont pour donner [7]
$$ \frac{V_x(t_0+dt)-V_x(t_0)}{dt} = \frac{X(t_0+2dt)-2X(t_0+dt)+X(t_0)}{(dt)^2} = \ddot{X}(t_0) \quad\quad\quad\quad (5) $$
Finalement en rapprochant l’expression (5) valable quelque soit
$t_0$ du système d’équations (2), en omettant l’indice $0$ pour alléger la notation (c’est-à-dire que l’on remplace $t_0$ par $t$) et en généralisant aux 2 autres coordonnées ($Y$ et $Z$), il vient :
$$ \boxed{ \begin{align*} \ddot{X}(t) &= 0\\ \ddot{Y}(t) &= -g \\ \ddot{Z}(t) &= 0 \end{align*} } \quad(\mathrm{pour\ toute\ valeur\ de\ } t) \quad\quad\quad(6) $$
La solution
Prenons la première équation de (6), nous pouvons utiliser (4) en remplaçant respectivement $t$ par $t^\prime$ et $t_0$ par $t$, ainsi pour toutes valeurs de $t$ et $ t^{’}$, on a :
$$ X(t^{’}) = X(t) + (t^{’}-t) \dot{X}(t) + \frac{1}{2}(t^{’}-t)^2 \ddot{X}(t) + \dotsb \quad\quad\quad(7) $$
On en déduit alors que la vitesse en $t^{’}$ a pour expression développée
$$ V_x(t^{’}) = \frac{X(t^{’}+dt)-X(t^{’})}{dt} = \dot{X}(t) + ( t^{’}-t)\ddot{X}(t) + \dotsb \quad\quad\quad (8) $$
Mais, le lecteur curieux a remarqué que (7) peut très bien s’écrire en remplaçant la fonction $X(t)$ par la fonction $V_x(t)$ comme suit
$$ V_x(t^{’}) = V_x(t) + (t^{’}-t) \dot{V}_x(t) + \frac{1}{2}( t^{’}-t)^2 \ddot{V}_x(t) + \dotsb \quad\quad\quad (9) $$
En identifiant terme à terme (8) et (9), on obtient les relations
$$ \begin{align*} V_x(t) &= \dot{X}(t) \\ \dot{V}_x(t) &= \ddot{X}(t) \quad\quad\quad(10) \end{align*} $$
Donc de (6), on en déduit
$$ \boxed{ \begin{align*} V_x(t^{’}) &= V_x(t) \\ V_y(t^{’}) &= V_y(t)-g(t^{’}-t) \\ V_z(t^{’}) &= V_z(t) \end{align*} }\quad (\mathrm{pour\ toute\ valeur\ de\ } t \mathrm{\ et\ } t^{’}) \quad\quad\quad\quad (11) $$
Première conséquence, comme la vitesse initiale est contenue
dans le plan (x,y) car $V_z(t=0) = 0$, alors la vitesse ultérieurement reste dans ce même plan. D’où
$$ Z(t) = z_0 \quad\quad\quad\quad (12) $$
Si maintenant on particularise (11) avec $t=0$ et que par soucis d’économie de notation on remplace $t^{’}$ par $t$, cela donne en se souvenant des valeurs initiales de la vitesse
$$ \begin{align*} V_x(t) &= V_x(0) = v_0 \cos\theta_0 \\ V_y(t) &= V_y(0) -g t = v_0 \sin\theta_0 - g t \quad(\mathrm{pour\ toute\ valeur\ de\ } t) \quad\quad\quad\quad (13) \end{align*} $$
La première égalité peut être injectée dans l’expression (7) où primo on a effectué le même type de changement d’arguments de la fonction que précédemment, et secundo en s’est servi des relations (10). Ainsi,
$$ X(t) = x_0 + t v_0 \cos\theta_0 \quad\quad\quad\quad (14) $$
De même pour la coordonnée $Y$, nous trouvons :
$$ Y(t) = y_0 + t v_0 \sin\theta_0 - \frac{1}{2} t^2 g \quad\quad\quad\quad (15) $$
Ainsi, nous avons trouvé les équations régissant l’évolution temporelle des coordonnées du centre de gravité de la flèche (en se souvenant $x_0=z_0=0$) :
$$ \boxed{ \begin{align*} X(t) &= v_0 \cos\theta_0 t \\ Y(t) &= y_0 + v_0 \sin\theta_0 t - \frac{1}{2} g t^2 \\ Z(t) &= 0 \end{align*} }\quad\quad\quad\quad (16) $$
Plus simplement…
Avant d’aller plus avant, remarquons que le raisonnement que nous avons utilisé avec les développements infinitésimaux du type (7), (9) etc peuvent être rigoureusement justifiés et accélérés en utilisant le calcul intégral introduit dans l’article Dynamique (simple) d’une fléche en phase de propulsion. En effet, finalement nous aurions pu écrire (2) comme :
$$ \frac{dV_x}{dt} = \frac{dV_z}{dt} = 0 \quad\quad \frac{dV_y}{dt} =-g $$
qui en intégrant une première fois sur l’intervalle $[0,t]$ donne les fonctions $V_x(t)$, $V_y(t)$ et $V_z(t)$ :
$$ \begin{align*} V_x(t) = \frac{dX}{dt} &= V_{0x} \\ V_y(t) = \frac{dY}{dt} &= V_{0y} - g t \\ V_z(t) = \frac{dZ}{dt} &= V_{0z} \end{align*} $$
et en intégrant une deuxième fois pour obtenir les fonctions $X(t)$, $Y(t)$ et $Z(t)$ :
$$ \begin{align*} X(t) &= x_0 + V_{0x} t \\ Y(t) &= y_0 + V_{0y} t - \frac{1}{2} g t^2 \\ Z(t) &= z_0 + V_{0z} t \end{align*} $$
ce qui est identique au système (16) une fois remplacé les valeurs initiales de la position $(x_0 = 0 ,y_0, z_0=0)$ et de la vitesse $( V_{0x}, V_{0y}, V_{0z} = 0)$ .
Nous utiliserons par la suite ce calcul intégral plus rapide et que nous avons justifié autant que faire ce peu…
De quelle trajectoire s’agit-il ?
Or donc, la trajectoire du centre de gravité de la flèche ou plus simplement par abus de langage la trajectoire de la flèche, est régit par le système (16). Mais, la première équation lie $X(t)$ à $t$ d’une manière linéaire (même proportionnelle car $x_0=0$) donc à chaque instant
$$ t = \frac{X(t)}{v_0 \cos\theta_0} \quad\quad\quad\quad (17) $$
que nous réinjectons dans l’expression de $Y(t)$ pour donner la relation entre les coordonnées $X$ et $Y$ quelque soit l’instant $t$ que nous omettons pour alléger les notations :
$$ \boxed{ Y = y_0 + \tan \theta_0 X - \frac{1}{2} \frac{g}{v_0^2\cos^2\theta_0} X^2 } \quad\quad\quad\quad (18) $$
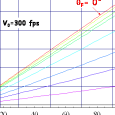
La trajectoire de la flèche est une
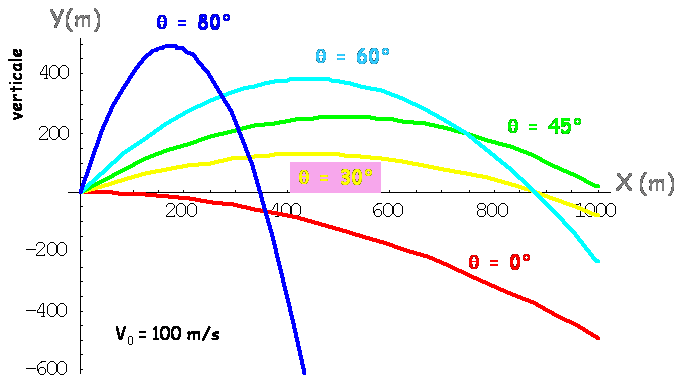
Premières constatations, pour $\theta_0 > 0$, la flèche commence par monter, puis après avoir atteint un maximum, elle redescend pour recroiser l’altitude du départ à une distance double (en $X$) de sa position au maximum. On note également que pour $\theta_0 = 30^\circ$ et $\theta_0=60^\circ$ la trajectoire recoupe l’altitude initiale pour la même valeur de $X$, et il semble que pour $\theta_0 = 45^\circ$ la flèche décrit sa plus longue portée.
Ces constations expérimentales vont être vérifiées et précisées ci-après. Si, la flèche atteint un maximum en $Y=y_m$ pour $X=x_m$, cela se traduit par le fait que (rappel : relation (7) avec la fonction $X(t)$ changée en $Y(X)$ et $\dot{u}(x) = du/dx$, $\ddot{u}(x) = d^2u/dx^2$...) :
$$ Y(x_m+dx) = y_m + dx \frac{dY}{dX}(x_m) + \frac{1}{2} dx^2 \frac{d^2Y}{dX^2}(x_m) + \dotsb \leq y_m $$
pour n’importe quel petit déplacement $dx$ (positif ou négatif) autour de $x_m$. Ce qui implique :
$$ \boxed{ \frac{dY}{dX}(x_m) = 0 \quad \mathrm{ et } \quad \frac{d^2Y}{dX^2}(x_m) < 0 } \quad\quad\quad\quad (19) $$
La première relation de nullité donne l’expression de $x_m$ car à partir de (18) la dérivée première par rapport à X donne :
$$ \frac{dY}{dX}(x_m) = \tan \theta_0 - \frac{g}{v_0^2\cos^2\theta_0} x_m $$
D’où [8]
$$ \boxed{ \begin{align*} x_m &= (v_0^2 /2 g) \sin 2\theta_0 \\ y_m - y_0&= x_m \tan\theta_0/2 \end{align*} } \quad\quad\quad\quad (20) $$
Nous pouvons réécrire (18) à l’aide des expressions de $x_m$ et $y_m$, il vient
$$ \boxed{ \frac{Y-y_0}{y_m-y_0} = 2 \frac{X}{x_m}\left( 1 - \frac{X}{2x_m}\right) } \quad\quad\quad\quad (21) $$
Deux propriétés découlent de cette formulation plus claire :
- si l’on pose $X = x_m (1 + u)$ alors après un peu de manipulation algébrique simple, on obtient l’expression
$$ \frac{Y-y_0}{y_m-y_0} = 1 - u^2 \quad\quad\quad\quad (22) $$
qui montre clairement la symétrie $(u,Y) \leftrightarrow (Y,-u)$ , c’est-à-dire
- la courbe repasse par la même altitude $Y=y_0$ à une portée, c’est-à-dire $X=x_F$, telle que (cf. le membre de droite nul) :
$$ x_F = 2 x_m $$
C’est une autre conséquence de la symétrie de la courbe ci-dessus mentionnée. Donc, la portée à une expression en fonction des paramètres initiaux
$$ \boxed{ x_F = \frac{v_0^2 }{g}\sin 2\theta_0 } \quad\quad\quad\quad (23) $$
Les propriétés de la fonction $\sin 2\theta$ dont le graphe est présenté ci-dessous
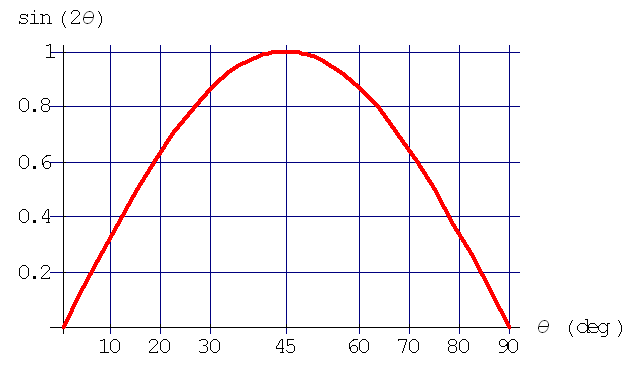
induisent deux conséquences :
-
- il existe une valeur maximale de la portée atteinte
$$ \boxed{ x_F^{max} = \frac{v_0^2 }{g} \quad (\theta_0 = 45^\circ) } \quad\quad\quad\quad (24) $$
Par exemple, $v_0 = 100 $m/s cela donne $x_F^{max} \approx 1019$
m.
-
- la symétrie de la fonction $\sin 2\theta_0 $ selon la transformation $\theta_0 \leftrightarrow 90^\circ -\theta_0$ montre qu’il existe 2 trajectoires qui passent par à la même altitude qu’initialement à la même portée $x_F$ (cf. sur les deux courbes $\theta_0 = 30^\circ$ et $\theta_0 = 60^\circ$ sur le schéma Différentes trajectoires paraboliques) . On peut donc atteindre son but par deux trajectoires, cela peut être intéressant s’il y a un obstacle qui empêche l’utilisation du tir tendu. Mais si sur un pas de tir FITA vous voyer un archer pointer le zénith, fuyez !
Pour finir cette section, notons que l’inégalité (19) est en fait respectée automatiquement car
$$ \frac{d^2Y}{dX^2}(X) = -\frac{g}{v_0^2 \cos^2\theta_0} \leq 0 $$
pour toute valeur de $X$ donc en particulier $x_m$ cela tient au fait que la force de pesanteur est dirigée vers le bas (ouf on l’a échappé belle !).
Résumé et perspectives
Nous avons défini les conventions permettant de déterminer dans cet article l’équation de la trajectoire de la flèche uniquement soumise à la force de pesanteur. Dans la seconde partie (Dynamique d’une fléche en phase de vol (Partie II)) nous aborderons des cas concrets afin d’envisager les conditions (angle initial de la flèche) pour atteindre son but. Donc à suivre...