Introduction
Cet article commence une petite série sur le modèle des articles sur la propulsion et la dynamique du vol d’une flèche. Le thème abordé cette fois concerne les oscillations de la corde après son lâché dans différentes conditions de leste. Les études qui vont suivre ont été motivées par les discussions à propos des masselottes que l’on voit ici ou là sur les cordes de certains arcs à poulies.
Avant de commencer à étudier ce sujet, je me souvenais de mes cours mais je pensais naïvement que le problème de l’influence des masselottes pas du tout d’actualité. En fait, certes si les premiers travaux datent du 19eme siècle comme ceux de von Helmholtz et de Laplace, des travaux de ces 10 dernières années ont été menés afin de comprendre les stabilités de surfaces comme les membranes élastiques et capillaires. Je ne rentrerai pas dans le domaine d’étude des surfaces mais comprenons que les cordes lestées donnent une vision de ce qu’il se passe à 1-dimension… Bref, j’ai trouvé l’inspiration dans des travaux de 2007.
Le formalisme va être un peu difficile, j’en conviens, et s’adresse à un public averti en particulier sur la résolution des équations différentielles que j’ai pu déjà aborder lors de la série sur le vol de flèche. Cependant j’espère qu’à la fin de la présente série, le lecteur pourra avoir une idée du comment et pourquoi sa corde oscille et quelle est l’influence des répartitions des masses le long de la corde. Après les questions seront les bienvenues, et les expériences/expérimentations des uns et des autres pourront amener de nouvelles études. Alors en avant !
Etablissement de l’équation différentielle des ondes (1-dim)
Figure 1 Schéma des forces agissant sur un petit élément de la corde
Pour établir les équations du mouvement de la corde, on va considérer le schéma de la figure 1en faisant l’hypothèse que la corde ne se déplace que dans un plan 2D essentiellement défini par l’axe qui joint l’attache de la corde aux branches (les Cams pour un arc à poulies) et l’axe de propulsion de la flèche. La décoche mécanique permet de se rapprocher de cette hypothèse, alors que la décoche manuelle influe sur le mouvement latéral de la corde. Egalement le poids de la corde est négligé face à la tension T interne de la corde : la tension est de plusieurs 10aines de kg alors que le poids de la corde est plutôt de l’ordre de 0.01kg ( 10 grammes).
L’élément de corde compris entre [x, x+dx] matérialisé en rouge est soumis à ses deux extrémités aux tensions des parties de corde en amont et en aval, notées $T(x)$ et $T(x+dx)$ . Les angles de ces 2 tensions par rapport à l’axe des abscisses sont notés $\theta(x)$ et $\theta(x+dx)$. Dans toutes ces notations $dx$ est infinitésimal c’est-à-dire $dx \ll 1$.
Si on projette sur l’axe des abscisses la force totale qui s’exerce sur l’élément de corde et égale à
$$ \begin{align*} dF_x &= T(x+dx) \cos[\theta(x+dx)] – T(x) \cos[\theta(x)]\\ &= \left( T(x) + \frac{\partial T(x)}{\partial x} dx \right)\left( \cos[\theta(x)] - \sin[\theta(x)]\frac {\partial \theta(x)}{\partial x} dx \right) - T(x) \cos[\theta(x)]\\ &= \left( \cos[\theta(x)] \frac{\partial T(x)}{\partial x} - T(x) \sin[\theta(x)] \frac{\partial \theta(x)}{\partial x} \right) dx \end{align*} $$
L’utilisation de l’opérateur $\partial/\partial x$ n’est autre que la dérivée (partielle) selon la variable x, car sous entendu il y a une autre variable qui a été figée dans le dessin à savoir le temps (t). Donc toutes les fonctions $T$,$ u$, $\theta$, $F_x$ sont des fonctions à la fois de x et de t.
En toute généralité, le terme entre parenthèse dans l’expression finale de la force longitudinale $dF_x$ n’a aucune raison d’être nul. Il est donc responsable de mouvements longitudinaux de l’élément de corde. Si on cherche la condition pour que $dF_x = 0$ alors la tension varie exactement selon $T(x) = T_0/\cos[\theta]$. D’habitude il est fait mention d’une approximation des petits angles et donc la tension est constante le long de la corde.
Sauf mention du contraire, on se placera par la suite dans l’hypothèse où les mouvements longitudinaux sont négligeables par rapport aux mouvements transverses.
Projetons selon l’axe transverse, en notant $f ^{’}(x) \equiv \partial f(x)/\partial x$ et ne gardant que les termes dominants (cf. gardant que les termes au plus d’ordre dx) et dans les fonctions trigonométriques (sin, cos), j’ai enlevé la dépendance en x quand elle n’est pas nécessaire :
$$ \begin{align*} dF_z &= T(x+dx) \sin[\theta(x+dx)] – T(x) \sin[\theta(x)]\\ &= T(x) \cos\theta\ \theta^{’} (x) dx + \sin\theta\ T^{’} (x) dx \end{align*} $$
L’évolution de la tension en fonction de l’angle permet d’écrire :
$$ dF_z = T_0 (1 + \tan^2\theta) \theta^{’}(x) dx $$
Or, en se reportant au dessin on peut écrire
$$ \tan\theta = \frac{u(x+dx)-u(x)}{dx} = \frac{\partial u(x)}{\partial x} $$
Et d’une manière générale la dérivée de la fonction tangente permet d’écrire
$$ \frac{\partial \tan \theta}{\partial x} = (1+\tan^2\theta) \theta^{’} (x) dx $$
Donc, sous l’hypothèse $dF_x = 0$, alors la force élémentaire transversale est donnée par
$$ dF_z = T_0 \frac{\partial^2 u(x)}{\partial x^2} dx $$
La force transversale est donc reliée à la courbure de la corde représentée par la dérivée seconde de la fonction $u(x)$ par rapport à x (toujours à t figé).
Maintenant, la loi de Newton liant force et accélération de l’élément de corde projetée sur l’axe transverse nous donne
$$ (\mu(x) dx) \frac{\partial^2 u(x,t)}{\partial t^2} = dF_z $$
Où $\mu(x)$ est la masse linéique (ou masse par unité de longueur) de l’élément de corde considéré. En exprimant $ dF_z $, on voit que $dx$ d’élimine et nous conduit à la fameuse équation différentielle des ondes à 1-dimension à savoir :
$$ \mu(x) \frac{\partial^2 u(x,t)}{\partial t^2} = T_0 \frac{\partial^2 u(x)}{\partial x^2} \quad\quad (Eq. 1) $$
Le rapport $T_0/\mu(x) = c(x)^2$ est homogène à une vitesse au carré.
Dans la suite la corde est supposée de masse linéique constante. Numériquement, une valeur typique est assez grande. En effet ; avec une tension de 50lbs (25kg=250 N), une longueur de l’ordre de 1 m et une masse de corde de 10 g, on obtient :
$$ c = \sqrt{\frac{T L}{m_c}} \approx \sqrt{\frac{250[N] \times 1[m]}{0.01[kg]}} \approx 160 [m/s] $$
Si une perturbation est crée localement sur la corde celle-ci se propage dans les 2 sens opposés avec la vitesse $c$, et en 1 seconde elle fait typiquement 80 allers-retours !
Exemple de résolution sans masselotte
Connaitre l’équation différentielle Eq.1 renseigne sur le couplage local entre l‘évolution longitudinale et l’évolution temporelle du déplacement transversal $u(x,t)$ de la corde. Mais pour connaitre l’expression (ou une estimation numérique) de ce déplacement pour tous les points de la corde et en fonction du temps, il est nécessaire (et suffisant) de donner un certain nombre de contraintes globales (ou d’ensemble) notée (Cg. 1) à savoir par exemple :
- les points de fixation de la corde aux deux bouts : $u(0,t) = u(L,t) = 0$ pour toute valeur de $t \geq 0$ ;
- la forme de la corde à l’instant 0 : $u(x,0) = f(x)$ ;
- et la vitesse de la corde à l’instant 0 : $v(x,0) = \frac{\partial u}{\partial t} (x,0) = g(x)$. Si on lâche la corde alors $g(x)=0$.
Pour résoudre le problème complet (Eq.1 + Cg.1), il est pratique d’étudier une famille de fonctions
$$ \Phi(x,t) = \left( A \sin[k x] + B\cos[k x] \right) \cos (\omega t + \phi) $$
Les 4 variables $A$, $B$, $k$ et $\omega$ sont à déterminer à partir de l’Eq. 1 et le jeux de contraintes globales Cg.1.
D’abord $\Phi(x,t)$ satisfait à l’équation d’ondes Eq.1 si
$$ -* \omega^2 \Phi(x,t) = - (c\ k)^2 \Phi(x,t) $$
et cela pour tout couple ($x,t$). Donc $\omega$ et $k$ sont contraints par la relation (dite de dispersion) :
$$ k = \frac{\omega}{c} $$
En passant si la corde n’est pas homogène (cf. ses caractéristiques dépendent de la position longitudinale) alors cette relation se modifie avec $\omega\rightarrow \omega(k)$ à savoir que la pulsation $\omega$ qui gouverne le rythme périodique en temps est une fonction non-proportionnelle du vecteur d’onde $k$ qui gouverne les oscillations spatiales. Je n’entrerai pas ici dans ce domaine d’étude.
Maintenant passons aux implications des contraintes globales Cg.1. Tout d’abord, considérons une vitesse initiale nulle quelque soit $x$ (cf. $g(x)=0$) alors
$$ \frac{\partial \Phi}{\partial t}(x,0) \propto \sin[\phi] \quad\quad \Rightarrow \phi = 0 $$
Ensuite, le point fixe en $x=0$ pour toute valeur de $t$ induit nécessairement
$$ \Phi(0,t) = B \cos[\omega t] \quad\quad\Rightarrow B = 0 $$
De même, le point fixe en $x = L$ pour toute valeur de $t$ impose
$$ \Phi(L,t) = A \sin[k\ L] \cos[\omega t] \quad\quad\Rightarrow \sin[k\ L]= 0 $$
En effet, conclure que $A = 0$ signifierait que la seule solution serait la corde au repos dans sa position initiale… Lâcher la corde et vous verrez quelle n’est pas immobile !
Non bien entendu $A\neq0$, par contre la contrainte ci-dessus n’est pas banale du tout et signifie que les valeurs de $k$ (et donc $\omega$) sont quantifiées, c’est-à-dire quelles prennent des valeurs discrètes car
$$ \sin[k\ L]= 0 \quad\quad\Rightarrow k = k_n = n \frac{\pi}{L} \quad\quad \mathrm{avec}\quad n=1,2,\dots $$
(ceux qui pensent que l’on fait de la mécanique quantique ici n’ont pas tord… mais ceci est une autre histoire)
Un petit récapitulatif : finalement les fonctions qui sont solutions à la fois de Eq.1 et Cg.1 sont du type :
$$ u(x,t) = \sum_{n=1}^{\infty} A_n \sin[n \pi \frac{x}{L}]\cos[n \pi \frac{c\ t}{L}] \quad\quad Eq. 2 $$
J’ai utilisé la linéarité de l’Eq.1 qui signifie dans notre cas que si $u_1(x,t)$ et $u_2(x,t)$ sont deux solutions alors pour tout couple de nombres réels $(\alpha,\beta)$, la fonction $\alpha\ u_1 + \beta\ u_2$ est également solution de l’Eq.1. D’où le signe somme $\sum$ qui fait courir l’indice $n$ sur toutes ses valeurs permises par la contrainte de point fixe en $x = L$.
L’expression Eq. 2 est le développement en série de Fourier de la fonction $u(x,t)$.
Chaque fonction sous le signe somme est très importante, on les appelle « mode » avec le fondamental pour $n = 1$ et les harmoniques pour les autres valeurs de $n$. Bien entendu la musique n’est pas loin avec les instruments à cordes… C’est dans ce cadre que von Helmholtz a étudié la perception des sons et la façon d’accorder les instruments.
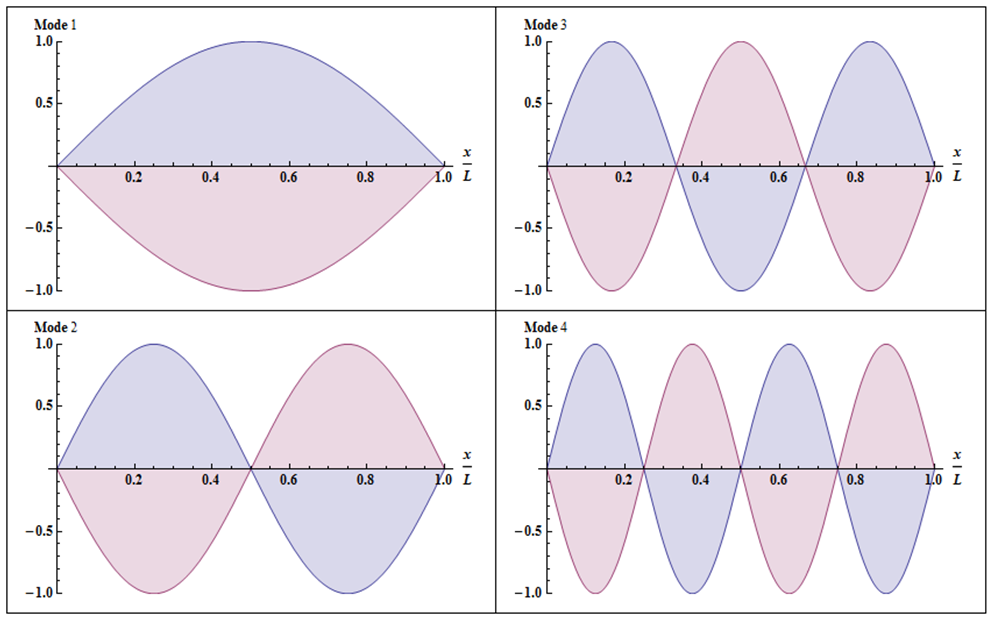
Sur la figure 2 sont représentées les 4 premiers modes avec pour chaque mode les 2 situations extrêmes données par le $\cos[\omega t] = \pm 1$. Les valeurs de $x$ pour lesquelles la fonction passe par $u(x,t) = 0$ s’appelle les nœuds, et l’on remarque que le nombre de nœuds (hormis les extrémités) sont au nombre de $n-1$ pour le Mode-$n$. Les positions de valeurs extrêmes sont quant à elles appelées des ventres.
Figure 2 Les 4 premiers modes d’une corde homogène : Mode 1 en haut à gauche c’est le mode "fondamental", ensuite en bas à gauche le Mode 2, et à droite les Modes 3 et 4.
Quand on excite périodiquement la corde avec un instrument vibrant, alors la corde vibre au rythme individuel de chaque mode, et on voit la corde osciller dans l’enveloppe des courbes bleues et roses de la figure 2. C’est un exercice très intéressant à faire, et plus spectaculaire avec une corde un peu élastique…
Bon, il reste une contrainte dans la liste Cg.1 : la forme initiale de la corde. Cette contrainte permet de fixer les coefficients $A_n$ de l’équation Eq. 2. Comment ? Cela tient à une propriété fondamentale des fonctions $\sin[n \pi x/L]$, en effet on dit quelles sont orthogonales à savoir quelles satisfont à la relation
$$ \frac{2}{L} \int_0^L \sin[n \pi x/L] \sin[m \pi x/L] dx = \delta_{n m} = \begin{pmatrix} 1 & \mathrm{si}\quad n = m \\ 0 & \mathrm{si}\quad n \neq m \end{pmatrix} $$
(note pour les lycéens : cela ressemble au produit scalaire entre vecteur et la condition d’ortho-normalité des vecteurs d’une base de l’espace…)
Donc, on peut se convaincre que les coefficients $A_n$ s’obtiennent par le calcul suivant :
$$ A_n = \frac{2}{L} \int_0^L \sin[n \pi x/L] f(x) dx $$
En regardant la figure 2, on se rend compte d’une propriété générale :
- si la fonction $f(x)$ est symétrique par rapport à $x = L/2$ (le milieu de la corde) alors seuls les coefficients impaires $A_{2p+1}$ ($p=0,1,\dots$) sont non nuls ;
- à l’inverse si la fonction $f(x)$ est anti-symétrique alors seuls les coefficients paires $A_{2p}$ ($p=0,1,\dots$) sont non nuls.
Par exemple prenons la fonction triangulaire suivante que nous retrouverons plusieurs fois car elle symbolise assez bien l’aspect de la corde à pleine allonge juste avant la décoche :
$$ f(x) = \left\{ \begin{array}{rl} 2\frac{H}{L}x & \mathrm{si}\quad 0 \leq x\leq L/2 \\ 2\frac{H}{L} (L-x) & \mathrm{si}\quad L/2 \leq x\leq L \end{array} \right. $$
Le calcul des coefficients $A_{2p+1}$ (p = 0,1…) donne
$$ A_{2p+1} = \frac{8 H}{\pi^2} \frac{(-1)^p}{(2p+1)^2} $$
On remarque que ces coefficients sont de plus en plus petits au fur et à mesure que $p$ augmente, et cela assez vite car $A_n \propto 1/n^2$. Le mode fondamental a le plus grand poids, d’où son nom… Numériquement parlant il est possible d’obtenir une très bonne approximation avec les 50 à 100 premiers termes de la série Eq. 2. Il faut dire que la troncature de la série pour obtenir une bonne approximation n’est pas toujours possible mais ceci est une autre histoire.
Donc finalement si on rassemble les éléments l’Eq.2 et l’expression des coefficients $A_n$, on obtient l’expression de la fonction $u(x,t)$ :
$$ u(x,t) = \frac{8 H}{\pi^2} \sum_{p=0}^{\infty} \frac{(-1)^p}{(2p+1)^2} \sin[(2p+1) \pi \frac{x}{L}]\cos[(2p+1) \pi \frac{c\ t}{L}] \quad\quad Eq. 3 $$
La figure 3 montre la forme de la corde « flashée » à différents instants en unité de $T = L/c$, t = 0, 1/10, 2/10,…, 9/10, 1.
Figure 3 Evolution de la corde lâchée dans la position trinagulaire en noir (trait plein).
Sur la première moitié du temps (de t = 0 à T/2 ), la corde est au dessus de sa position au repos (correspondant à l’axe des abscisses), la seconde moitié (de t =T/2 à T) la corde descend toujours, et ensuite en fait la corde remonte en suivant un chemin inverse à même vitesse. C’est donc bien un mouvement oscillant entre 2 positions extrêmes. D’autre part, on s’aperçoit que le point central de la corde se meut avec une vitesse constante alternant entre 2 extrêmes
$$ V(x=0) = \pm 2 c \frac{H}{L} = \pm 2 H \sqrt{\frac{T}{m_c L}} $$
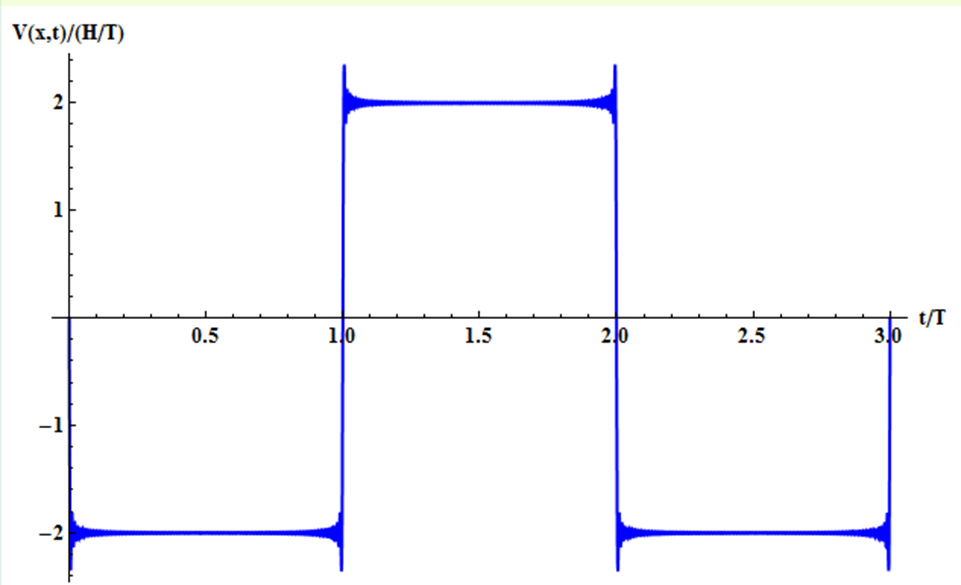
que l’on peut voir également sur le graphique de la figure 4.
Figure 4 Vitesse du point central en fonction du temps.
Ce type de configuration pourrait se passer lors d’un lâché sans flèche ! Mais même dans ce cas malheureux qui peut entrainer des dégâts au niveau du matériel, l’évolution de la corde au-delà de (t=T/2) serait modifiée car il faudrait tenir compte de la déperdition d’énergie que nous avons négligés qui sont dues aux efforts mécaniques internes à la corde et à l’émission d’ondes sonores par frottements avec l’air.
Il est intéressant de se rendre compte que numériquement la valeur de $T$ vaut environ 6ms (6 millièmes de seconde), donc le temps de retour à la position de repos se ferait en 3ms. Pourquoi est-ce intéressant, me direz-vous ? Et bien si on se souvient de Dynamique (simple) d’une fléche en phase de propulsion, le temps de propulsion d’une flèche est de l’ordre de 14ms ! On est bien dans les mêmes ordres de grandeur temporelle…
Résumé
Dans ce premier article d’une série dédiée aux oscillations de notre corde d’arc nous avons établi l’équation maîtresse (Eq. 1) d’évolution des déplacements transverses. Nous avons résolu le problème et déterminer l’évolution de la corde dans un cas qui ressemble à celui d’un lâché à pleine allonge. Numériquement, nous avons estimé la vitesse de propagation et le temps caractéristique de l’évolution oscillante que nous avons rapproché du temps de propulsion de la flèche. Mais l’évolution de la corde est un peu trop rapide, serait-ce qu’on aurait oublié quelque chose ? A suivre…