Introduction
Dans les articles Dynamique (simple) d’une fléche en phase de propulsion, Dynamique d’une fléche en phase de vol (Partie I), Dynamique d’une fléche en phase de vol (Partie II), Dynamique d’une flèche en phase de vol (partie III) et Dynamique d’une flèche en phase de vol (partie IV), j’ai écrit une série dédiée à la modélisation du vol d’une flèche dans différentes configurations
dont pour le dernier article la prise en compte de la force de trainée.
Tous ces développements ont été effectués avec ce que l’on appelle le formalisme de Newton des forces et des "Principes fondamentaux de la Dynamique". Isaac Newton l’a élaboré dans les années 1685, et si il y a eu une bataille de paternité sur l’invention du calcul infinitésimal entre lui et Gottfried Wilhelm Leibnitz, par contre il n’en reste pas moins que ce fût pour Newton un tour de force d’unifier pour la première fois la description du monde terrestre et celle du mouvement des planètes et des comètes.
A propos de comètes, la fameuse « Comète de Halley », avait été vue en 1531, 1682 et Edmond Halley avait prévu son retour en 1758, cependant les calculs de J. de Lalande et N-R. Lepaute basés sur la théorie de Newton et prenant en compte le passage prés de Jupiter, lesquels calculs leur prirent 1 mois, avaient prévu un retour pour avril 1759 à +/- 1 mois. L’Observation le 13 Mars 1759 fût considérée comme le premier grand succès de la théorie de Newton [1].
Cependant, malgré ce succès, il a fallu tout un travail de reformulation des Principes de Newton pour que ses idées soient vraiment et complètement acceptées. Dans ce long parcours, je vais m’arrêter sur les travaux des mathématiciens et astronomes Leonhard Euler (suisse) et Joseph-Louis Lagrange (italien naturalisé français) q’ils ont établi dans les années 1750. Ces méthodes développées dans un cadre que l’on qualifie maintenant de classique, sont au coeur des développements en Théorie Quantique des Champs dont la physique des particules élémentaires.
Le Lagrangien
Un rappel, selon le formalisme de Newton, on se demande quelles sont les forces qui s’appliquent à la flèche en cours de vol [2] pour écrire selon le Principe Fondamental de la Dynamique l’équation du mouvement :
$$ \frac{d\vec{p}}{dt} = m\vec{g} $$
avec $\vec{p}=m\vec{v}$ le vecteur quantité de mouvement de la flèche de masse $m$ et de vitesse $\vec{v}$, et $m\vec{g}$ le poids de la flèche dirigé selon l’accélération de la pesanteur locale $\vec{g}$ d’intensité typique de $9.81 \mathrm{m.s^{-2}}$ au nivau de sol.
Avec Lagrange, et le formalisme de la Mécanique Analytique, on va premièrement se poser la question de trouver une fonction, le lagrangien, qui va dépendre en toute généralité
- des variables de positions notées ($q_i$) comme par exemple $(x,y)$ dans la cas de notre flèche
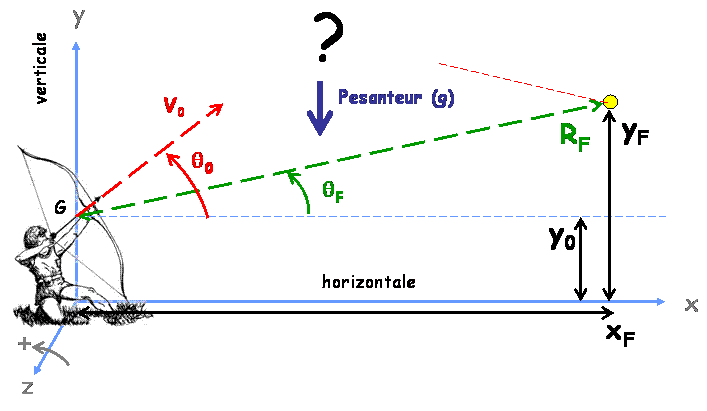 Repère des positions et des angles
Repère des positions et des angles - des variables de vitesses, c’est-à-dire de la dérivée des positions par rapport au temps, notées $(\dot{q}_i)$ ;
- et du temps lui-même explicitement (c’est-à-dire non pas indirectement à travers la dépendance temporelles des positions et vitesses)
Dans la suite on ne considère que le cas où le lagrangien ne dépend pas explicitement du temps (cf. $ \partial \mathcal{L}/\partial t = 0$) c’est-à-dire des cas non-dissipatifs (cf. l’énergie totale est conservée).
Donc, on se donne a priori le lagrangien
$\mathcal{L}(q_i, \dot{q}_i$ q’il va être judicieux de choisir selon une forme qui dépend de l’énergie cinétique et de l’énergie potentielle de la flèche à savoir [3] :
$$ \boxed{ \mathcal{L}(q_i, \dot{q}_i) = \mathcal{L}(x,y ;\dot{x}, \dot{y})= E_c - E_p = \frac{1}{2} m (\dot{x}^2+\dot{y}^2) - m g y } $$
(il y a bien le signe "-" entre l’énergie cinétique et l’énergie potentile). On note au passage que le lagrangien dans cet exemple ne dépend par de $x$ explicitement, nous reviendrons sur ce constat d’ici peu.
Le Principe Variationnel d’Hamiltion, Eq. d’Euler-Lagrange
Une fois établi le lagrangien (il n’est pas unique) qui remplace la liste des forces extérieures dans le formalisme de Newton, le second ingrédient du formalisme lagrangien est le Principe Variationnel d’Hamilton (de William Rowan Hamilton mathématicien et astronome irlandais) qui remplace le Principe Fondamental de la Dynamique. Ce nouveau principe stipule que l’équation du mouvement (de la flèche) entre deux instants $t_1$ et $t_2$
réalise un minimum de l’Action définie par :
$$ \mathcal{A}[q](t_1,t_2) = \int_{t_1}^{t_2} \mathcal{L}(q_i, \dot{q}_i, t)\ dt $$
$\mathcal{A}$ est une fonction implicite des fonctions $q_i(t)$ du mouvement. Une fonction de fonctions s’appelle une fonctionnelle, et de même que l’on définit des dérivées par rapport à des variables (exemple $f^\prime(x) = df(x)/dx$, ou $\dot{f}(t)=df(t)/dt$), on définit également des dérivées par rapport à des fonctions.
De ce Principe Variationnel, on en déduit les équations d’Euler-Lagrange :
$$ \boxed{ \frac{d}{dt}\left( \frac{\partial \mathcal{L}}{\partial \dot{q}_i}\right) - \frac{\partial \mathcal{L}}{\partial q_i} = 0 \qquad \forall i } $$
Pour lire cette formule il faut distinguer ce que l’on appelle une dérivée totale que l’on note avec des "d-droits" (cf. $d$), et une dérivée partielle que l’on note avec des $\partial$ qui sont des "d-courbes". La différence fait sens quand on manipule des fonctions à plusieurs variables. Prenons par exemple une fonction $f$ à 2 variables, $f(x,y)$. On peut se demander comment varie la fonction si $x$ varie, tout en gardant $y$ fixe, on définit alors la dérivée selon $x$ comme :
$$ \left( \frac{\partial f}{\partial x} \right)_y (x,y) = \underset{h\to 0}{\lim}\ \left( \frac{f(x+h,y)-f(x,y)}{h} \right) \equiv \frac{\partial f}{\partial x} $$
Sauf cas d’ambiguïté, on omet de mentionner que $y$ est fixé, ce qui donne la dernière notation. On définit symétriquement la dérivée selon $y$ quand $x$ et fixé, et l’on étant au dérivée d’ordre supérieure. On montre que prendre successivement la dérivée selon $x$ puis la dérivée selon $y$, revient identiquement à prendre la dérivée selon $y$ suivi de celle selon $x$, c’est-à-dire que
$$ \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} $$
tout en se rappelant à chaque dérivée selon une variable, on garde les autres fixes.
Pour ce qui concerne la dérivée totale, elle intervient dans la problématique où à la fois $x$ ET $y$ changent en même temps. par exemple si $x$ change en $x+dx$ et $y$ en $y+dy$ alors la fonction $f$ va passer de $f(x,y)$ à $f(x,y)+df$, où $df$ est la dérivée totale de $f$. On montre que
$$ df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy $$
Si par exemple, la variation de $x$ et $y$ se fait à travers le temps $t$, alors la dérivée totale de $f$ par rapport au temps $t$ est égale à :
$$ \begin{align} \frac{df}{dt} &= \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt} \\ & = \frac{\partial f}{\partial x} \dot{x} + \frac{\partial f}{\partial y} \dot{y} \end{align} $$
Application au vol de la flèche
Dans le cas du vol de la flèche, les équations d’Euler-Lagrange sont au nombre de 2 puisque les $q_i$ ne sont autres que $x$ et $y$, donc il vient
$$ \begin{align} \frac{d}{dt}\left( \frac{\partial \mathcal{L}}{\partial \dot{x}}\right) - \frac{\partial \mathcal{L}}{\partial x} &= 0 & (1) \\ \frac{d}{dt}\left( \frac{\partial \mathcal{L}}{\partial \dot{y}}\right) - \frac{\partial \mathcal{L}}{\partial y} &= 0 & (2) \end{align} $$
La remarque que nous avons faites dans la section précédente à propos du fait que le lagrangien ne dépend pas explicitement de la variable $x$ prend tout son sens quand on regarde l’équation (1) ci-dessus. En effet, ne dépend pas explicitement de $x$, signifie que sa dérivée partielle par rapport à $x$ est nulle, donc l’équation (1) devient :
$$ \frac{d}{dt}\left( \frac{\partial \mathcal{L}}{\partial \dot{x}}\right) = 0 \Rightarrow \frac{\partial \mathcal{L}}{\partial \dot{x}} = m \dot{x} = Cte $$
C’est-à-dire que non seulement l’énergie totale de la flèche est une constante du mouvement, mais il en est de même de la quantité de mouvement selon l’axe $x$, comme $m$ est constant, il en est donc de même de la vitesse selon $x$. Donc, par il vient par intégration simple, que le mouvement selon l’axe $x$ est régit par l’équation en fonction du temps $t$ connaissant les valeurs de la position et la vitesse à l’instant $t=0$ :
$$ \dot{x}(t) = \dot{x}(0) \Rightarrow x(t) = \dot{x}(0) t + x(0) $$
L’équation (2) quant à elle explicite le mouvement selon la verticale :
$$ \frac{d}{dt}(m \dot{y}) = - m g $$
Gardant à l’esprit que $m$ est une constante, alors
par 2 intégrations successives cette fois, on a :
$$ \begin{align} \dot{y}(t) &= -g t + \dot{y}(0) \\ y(t) &= - \frac{1}{2}g t^2 + \dot{y}(0) t + y(0) \end{align} $$
Et en éliminant la variable temps, l’équation qui relie $y$ et $x$ est donnée par
$$ \boxed{ y = y(0) + \tan \theta_0\ x - \frac{1}{2} g \left( \frac{x}{v_0 \cos \theta_0} \right)^2 } $$
si $x(0) = 0$ soit l’origine de l’axe horizontal, $\theta_0$ désigne l’angle de la vitesse initiale avec l’axe horizontal, et $v_0$ l’intensité de la vitesse initiale. On retrouve bien l’équation établie dans l’article Dynamique d’une fléche en phase de vol (Partie I).
Résumé et perspectives
Dans cet article, je vous ai montré comment le formalisme de Newton avec le concept de Force et son Principe de la Dynamique, a été transformé quasiment un siècle plus tard, par le concept de Lagrangien adossé au Principe Variationnel qui donne les équations d’Euler-Lagrange du mouvement. Le formalisme alternatif a trouvé son cadre dans la Mécanique Analytique tout d’abord en Mécanique Classique, puis en Mécanique Relativiste (Restreinte et Générale) et des développements ultérieurs ont donné lieu à 2 cadres théoriques "quantiques" :
- l’Hamiltonien qui n’est autre qu’une nouvelle formulation pour les problèmes invariants par translation dans le temps, dont l’axiomatisation ultérieure en termes d’opérateurs de positions et quantité de mouvement a donné le cadre de la Mécanique Quantique actuelle ;
- et quand on remplace les variables $q_i$ par des fonctions $\psi(\vec{x},t)$ qui dépendent des 4 variables d’espaces-temps que l’on nomme des champs, alors s’élaboreront conjointement à la Mécanique Quantique, ce que l’on appelle la Théorie Quantique des Champs qui donne le cadre théorique par exemple du Modèle Standard de la Physique des Particules Élémentaires.