Introduction
Dans la liste des différents paramètres qui définissent les caractéristiques d’une flèche, outre sa longueur, sa masse..., il y a le spine. Ce paramètre est celui qu’essaye d’ajuster au mieux le vendeur d’archerie quand vous lui donner la puissance de votre arc et votre allonge. Il le fait en regardant par exemple le tableau EASTON dont l’article Comment lire les tableaux EASTON ? (tab. 2020) fait une description détaillée. Une version de ce tableau (ou d’autres) existe sous forme de logiciel décrit dans l’article Logiciels de choix de configurations arc-flèche.
Le spine est un nombre qui peut être mentionné sur le fut. Par exemple, on parle d’ACE 520, pour une flèche dont le spine est de 520. La gamme de spine est assez large par exemple pour les ACE on dispose de : 370, 400, 430, 470, 520, 570, 620, 670, 720, 780, 850, 920, 1000, 1100, 1250.
Mais une question se pose : à quoi correspond ce nombre exactement ?
Définition
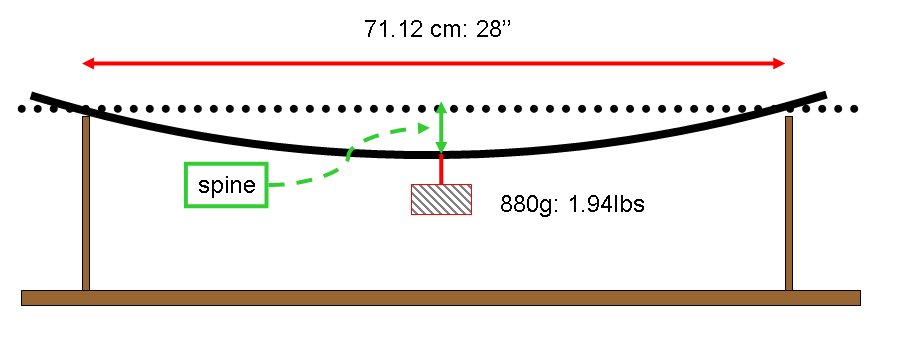
Le spne est une mesure de la déformation (on dit flèche d’ailleurs pour une poutre) que subit la flèche quand on lui applique une force en son milieu perpendiculairement à son axe de symétrie. Ceci dit, la déformation doit être mesurée dans une configuration spéciale. Un schéma éclaire le propos :
Le nombre (ex. 520) est la valeur de la déformation exprimée en millième de pouce et dans les conditions suivante : la charge est de 1.94lbs soit 880g , et la distance entre les appuis est de 28 pouces soit 71.12 cm.
Le spine renseigne sur la "souplesse" ou la "raideur" d’une flèche face à une charge statique, par opposition à ce que pourrait être une déformation à une sollicitation qui varie dans le temps (mouvement oscillatoire, ou bien forte accélération de poussée !).
La théorie des matériaux nous donne une relation entre le spine s, la force statique F s’appliquant au centre de la flèche, la distance entre les points d’appuis L :
$$ \boxed{ s = \frac{F L^3}{48 E I} } $$
où apparait au dénominateur :
- un paramètre géométrique I qui est le moment quadratique [1] de matière transverse qui s’exprime en fonction de l’épaisseur e et le diamètre extérieur du tube D par $ I = \pi/64 (D^4-(D- 2 e)^4) \approx \pi/8 D^3 e$ (la dernière expression n’est valable que si $e$ est négligeable devant $D$ ;
- et E est le module d’Young qui caractérise le matériau constituant la flèche, exprimée comme une pression (force par unité de surface) en MPa (méga-Pascal).
A titre d’exemple des ACE 520 :
- La force $F=0.880\times 9.80 = 8.624$N
- $s = 0.520$’’ ou $1.32$cm
- $I\approx 1.5 10^{-11}$ m$^4$
- $E\approx 3.4 10^5$ MPa (MPa = $10^6$Pascal)
La valeur du module d’Young est typique des matériaux à base de fibre de carbone de haute résistance, mais les valeurs dépendent vraiment des modes de fabrications exacts (voir plus d’informations sur le Module d’Young).
Spine-metre artisanal
Il est relativement aisé de se fabriquer un instrument qui permet de mesurer et contrôler le spine de ses flèches. Non pas que l’on veuille remettre en cause les valeurs "constructeurs" mais cet appareil peut servir par exemple :
- à mesurer le spine statique de ses flèches une fois coupées à son allonge,
- à vérifier que le spine de ses flèches ne varie pas dans le temps,
- à simplement mesurer le spine quand il n’y a pas d’indication du constructeur (sur les futs alu, et a forciori sur les futs bois).
Voici une version réalisée à partir des indications du site.
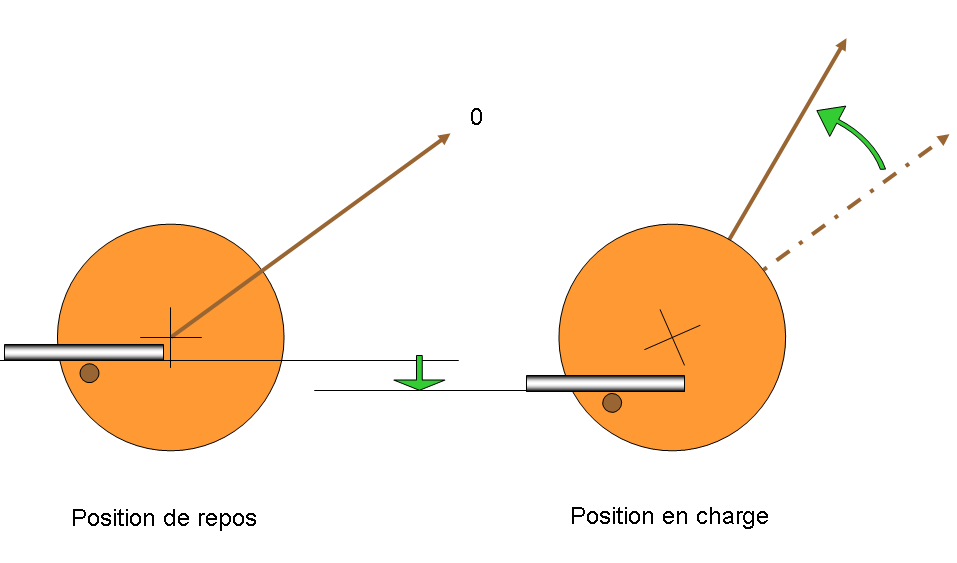
Le principe de fonctionnement est très simple. Après avoir mis en place les deux points d’appui pour y loger la flèche, le cœur du système tient dans le fonctionnement de la roue centrale où on a logé à sa périphérie un petit ergot cylindrique qui vient en contact avec le fut de la flèche. Lorsque la flèche est chargée en son milieu, celle-ci appui sur l’ergot qui descendant et fait pivoter la roue et donc la tige qui sert d’indicateur. Voici le schéma de principe :
On peut déjà utiliser telle quelle cette version pour noter la valeur de la déviation angulaire due à la flexion de la flèche soumise à une charge fixée et voir si toutes les flèches réalisées de la même façon se comportent indiquement. On peut également comparer des lots différents de flèches ayant a priori les mêmes caractéristiques pour savoir si c’est bien le cas...
Mais pour une mesure de spine il est nécessaire d’aller plus loin en passant par un étalonnage de l’appareil. Le schéma de principe un peu plus détaillé ci-dessous permet d’introduire les variables qui caractérisent le fonctionnement :
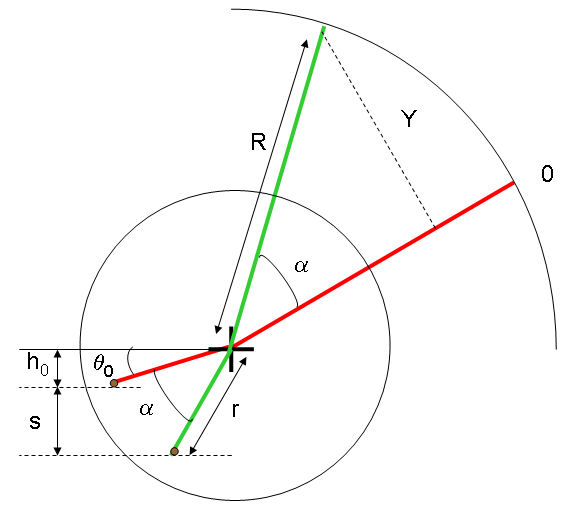
On s’aperçoit avec un peu de trigonométrie de 3eme que :
- $\sin\theta_0 = h_0/r$ coté ergot cylindrique au repos
- $\sin(\theta_0+\alpha) = (h_0 + s)/r$ coté ergot cylindrique en charge
- $\sin\alpha = Y/R$ exprimant la déviation angulaire de l’indicateur.
D’autre part, la relation définissant le spine, on en déduit la loi d’échelle suivante :
$$ s = s_0 \frac{M}{M_0}\left( \frac{L}{L_0}\right)^3 $$
exprimant la valeur du spine s réelle obtenue dans les conditions de fabrication de l’instrument (L) et l’utilisation d’une masse M en comparaison des valeurs théoriques (ou "constructeurs") indicées par un 0.
En mesurant, r, R, $\theta_0$, M, L on peut prédire la valeur de Y pour un spine théorique donné. Dans mon cas par exemple :
- $r = 37$mm, $R=230$mm, $\theta_0 =20^o $,
- $L=26’’$, $M=985$g, donc
- $Y = 84$mm (resp. 115mm) pour un spine théorique de 520 (resp. 690).
La photo ci-dessous montre que les mesures sont tout à fait en accord avec ces estimations ce qui permet de valider le modèle de fonctionnement du système et les valeurs des paramètres le caractérisant.

A partir de ce modèle il est ensuite simple de se faire une échelle graduée si besoin comme pour une balance.
Stabilité du spine
Avec le spine-metre décrit dans la section précédente, il est possible d’entreprendre quelques études sur la stabilité du spine "statique" :
- pour un lot de flèches
- en comparant deux lots de flèches
- après sollicitation mécanique d’une flèche
- vieillissement des flèches...
En comparant les spines de 12 ACE 520 fabriquées en 2009 et un autre lot de 2010, je peux dire que les fleches ont le même spine (précision de mesure relative $\pm 5$ unités). Deux lots même étiquetés "520" peuvent avoir une différence de spine de 10 unités. Il est remarquable que la tolérance constructeur (EASTON) sur les spines d’un même lot de 12 flèches est de $\pm 5$ unités également.
Pour ce qui est de la variation du spine statique lorsque la flèche est soumise à des sollicitations mécaniques, on peut faire la petite expérience suivante : bloquer les extrémités d’un fut et lui accrocher au milieu une corde qui par tension lui fait subir une déformation oscillante. Après avoir fait subir plus de 10000 déformations de 5cm, la mesure avant et après du spine statique n’a pas montré de différence. Cela va dans le sens que les mécaniciens connaissent bien : ce n’est pas par la mesure du module d’Young [2] d’un matériau que l’on peut se rendre compte qu’une pièce vieillit. La rupture d’une pièce est le résultat de défauts de surface qui par sollicitation vont se propager dans le matériau. Mais ces défauts de surface n’influe pas le module de Young sauf peut-être quand le nombre de cycles de sollicitations approche la rupture (mais trop tard...). Par contre la fréquence propre d’oscillation peut être affectée par ces défauts (à suivre).
Résumés et perspectives
Nous avons vu à quoi correspond le spine de nos flèches. Cette valeur mesure une déformation à la suite d’une mise en charge statique dans des conditions bien précises. Ce chiffre renseigne sur le produit du module d’Young intrinsèque au matériau utilisé et du moment d’inertie qui tient compte de la répartition de matière dans la section transverse de la flèche. Ces paramètres certes fondamentaux ne sont que des caractéristiques statiques de la flèche alors que la dynamique de la phase de propulsion est non seulement rapide mais sollicite la flèche d’une manière non négligeable (voir l’article Dynamique (simple) d’une fléche en phase de propulsion) à tel point que la flèche se met à onduler ce qui correspond au paradoxe de l’archer (La paradoxe de l’archer). On se penchera donc dans un prochain article sur la notion de spine dynamique.


































Commentaires Forum fermé