Introduction
L’usage d’un scope sur un arc à poulies

se fait dans la plus part des utilisations pratiques avec en parallèle une visette.

Il ne faut pas oublier cependant que l’archer voit avec son œil directeur auquel peut être adjoint des lunettes. Donc il faut considérer en toute généralité l’ensemble optique : œil-lunette-visette-scope. Les conditions d’utilisation de cet ensemble sont également à considérer, car tout archer a expérimenté les modifications de ses réglages suivant la luminosité (forte/faible) et le type d’éclairage (naturel/artificiel).
L’étude complète de la formation de l’image de la cible après le système optique scope-visette-[lunette]-œil est complexe et mérite plusieurs articles pour aller progressivement. Pour cet article voyons l’effet de la lentille du scope.
Construction de l’image par le scope
La lentille du scope est dite convergente, c’est à dire qu’elle concentre un faisceau de lumière idéalement en un point, le foyer (F). C’est pour cette raison qu’il ne faut absolument pas regarder le Soleil avec le scope (bien que nous y reviendrons à la fin de l’article, la distance focale des scopes dépassent en régle générale la longueur d’un bras noramalement constitué).
Dans la suite, nous allons utiliser une approximation qui se vérifie dés lors que les rayons lumineux sont proches de l’axe de symétrie du scope matérialisable par le passage de la fibre optique en (O) (voir la figure du scope ci-dessus). Cette approximation est d’autant mieux vérifiée qu’en général, on regarde des cibles qui sont à des distances bien plus grandes que la taille du scope et au rayon de courbure de la lentille... D’autre part, on utilisera également le fait que la lentille est mince (ou fine) en comparaison des dimensions du scope.
Dans ces conditions, on peut démontrer que les rayons lumineux émanants d’un objet plan (AB) (ex. la cible) se concentrent dans un plan de l’autre coté de la lentille pour former une image (A’B’).
Sur le schéma ci-dessous, on a représenté la façon dont on peut construire graphiquement l’image (A’B’).
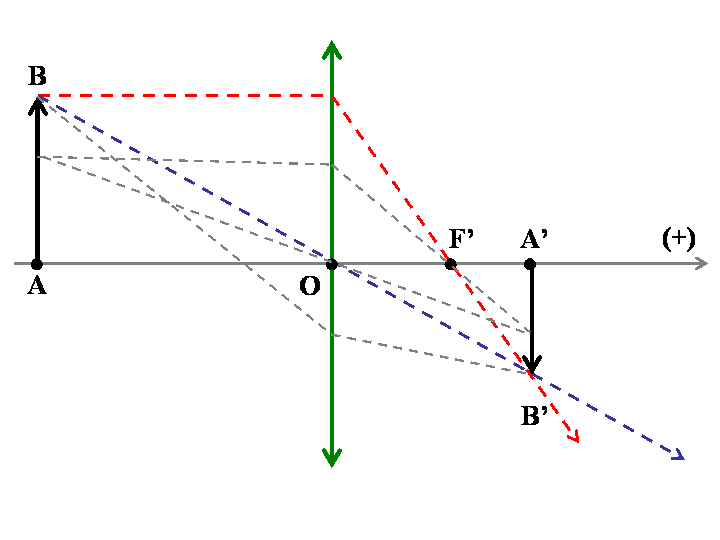
On a utilisé deux propriétés de la lentille convergente :
- tout faisceau parallèle à l’axe de symétrie (en rouge) émanant de l’objet sort de la lentille en direction du foyer (F’) (ici on utilise un ’ par analogie à la notation de l’image A’B’ ;
- tout faisceau passant par le centre optique de la lentille O (en bleu) n’est pas dévié ;
Ainsi, l’intersection des deux types de faisceaux permet de construire par exemple l’image B’ issue de B.
Comme on peut se rendre compte en procédant de proche en proche à la construction géométrique de tout point de AB, il apparaît l’image A’B’ comme annoncée.
Position de l’image
Pour aller un peu plus loin, surtout si l’on désire par exemple donner le grossissement du scope, nous allons utiliser un peu de mathématiques élémentaires.
Sur le schéma ci-dessus, nous avons orienté l’axe horizontal de telle façon que l’on compte positivement la distance à parcourir de A vers 0, et négativement celle pour aller de O vers A. On note la distance A vers 0 comme cela : $\overline{AO}$. Et par exemple si la distance que l’on mesurerait avec un décamètre est de 18 m, alors on a par définition du sens positif (+) mentionné :
$\overline{AO} = +18 $m et $\overline{OA} = -18 $m
On parle de longueur algébrique $\overlineOA dés lors que l’on introduit la notion d’axe orienté, sinon on parle de longueur tout simplement.
Si on introduit un autre point M par exemple sur l’axe (AO) alors en prenant les longueurs algébriques, on a la propriété trés simple :
$$ \overline{OA} = \overline{OM} + \overline{MA} $$
et cela peut importe si M se trouve entre O et A, ou bien ailleurs car les signes comptent correctement des différentes situations relatives des 3 points. Super, non ?
Revenons à notre image A’B’, il serait intéressant de connaître sa position sur l’axe horizontale, c’est-à-dire de savoir calculer $\overline{OA’}$ qui selon le schéma est .... positive ! Bravo tout le monde suit !
Et bien en utilisant les propriétés des triangles (c’est simple l’optique...), nous pouvons écrire la relation [1] :
$$ \boxed{ \frac{1}{\overline{0A}} - \frac{1}{\overline{0A’}} = - \frac{1}{\overline{0F’}} }\quad\quad \quad\quad (1) $$
Maintenant introduisons quelques notations :
- $L>0$ : la distance entre la cible et la lentille du scope
- $\delta_{s}>0$ : la vergence de la lentille du scope dont l’unité est dioptrie qui par définition l’inverse du métre, c’est-à-dire $1/m$, ou $m^{-1}$. La vergence n’est rien d’autre que l’inverse de la longueur OF’ [2].
Si on reporte ces notations dans la formule (1), il vient :
$$ \frac{1}{L} + \frac{1}{\overline{0A’}} = \delta_{s} $$
Donc notre premier objectif est atteint, l’image est située à une distance algébrique du centre O :
$$ \boxed{ \overline{0A’} = \frac{L}{L\delta_{s}-1} }\quad\quad\quad\quad (2) $$
Si typiquement, $\delta_{s} \approx 1$ m et $L \approx 10:100$ m alors $\overline{0A’} \approx 1/\delta_{s} >0$
C’est-à-dire que l’image est proche de la position du foyer image de la lentille. Mais restons un peu général avant de faire des applications numériques, surtout que la position de l’image n’est pas une fin en soit (sauf pour les narcissiques bien entendu)
Grossissement du scope
L’image A’B’ est vue par l’oeil de lynx de notre archer [3], lequel est situé à une certaine distance du scope. Soit
- $\ell>0$ : la distance entre la lentille du scope et l’oeil de l’archer
Si l’on compare l’aspect de la cible selon qu’on la regarde à l’oeil nu ou à travers le scope, on se trouve dans les deux situations du schéma ci-dessous :
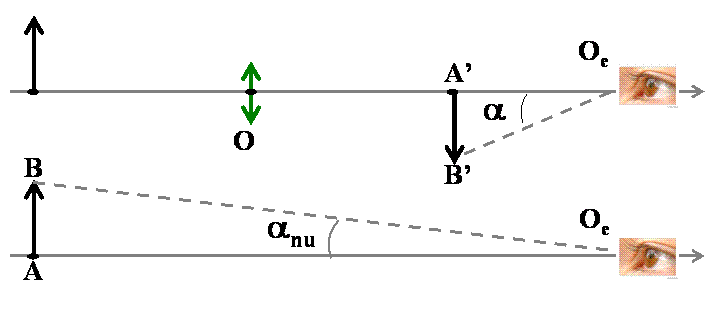
c’est-à-dire que l’oeil va voir
- soit l’image en directe selon un angle $\alpha_{nu}$
- soit l’image produite par le scope selon un angle $\alpha$
On définit alors le grossissement du scope comme étant le rapport :
$$ G_{scope} \equiv \frac{\alpha}{\alpha_{nu}} $$
Si on se souvient que nous travaillons avec l’hypothèse de petit angle, alors
$$ \alpha_{nu} = \frac{AB}{L+\ell} \equiv \frac{AB}{D} $$
On note la distance $D = L+\ell$ non seulement pour simplifier la formule mais également parcequ’on se rend compte que D est la distance à la cible à quelque chose prés (ex. 18, 30, 50, 70 m).
Dans la configuration où l’image est vue à travers le scope, on a
$$ \alpha = \frac{A’B’}{0_{e}A’} $$
Or, par la propriété des triangles semblables, il vient
$$ \frac{A’B’}{AB} = \frac{OA’}{OA} = \frac{0A’}{L} $$
D’où
$$ \alpha = \left( \frac{AB}{L}\right) \left( \frac{0A’}{0_{e}A’}\right) = \left( \frac{AB}{L}\right) \left(\frac{0A’}{0A’ - \ell}\right) $$
En ce servant de la formule donnant OA’ à la section précédente, il vient après avoir fait un peu d’algèbre, finalement
$$ \boxed{ G_{scope} = \frac{1}{1-\ell(1-\frac{\ell}{D})\delta_{sc}} \approx \frac{1}{1-\ell\delta_{sc}} }\quad\quad\quad\quad (3) $$
où la dernière approximation tient compte du fait que généralement $\ell< 1 $ m alors que $D > 10$ m et que donc on peut considérer que $\ell/D \ll 1$.
Applications numériques
Il est remarquable que si la distance entre le scope et l’oeil est du même ordre de grandeur que la longueur focale (= inverse de la vergence), ce qui se traduit par $\ell\approx 1/\delta_{sc}$ alors le grossissement G tend vers l’infini, tout du moins selon les approximations utilisées ici.
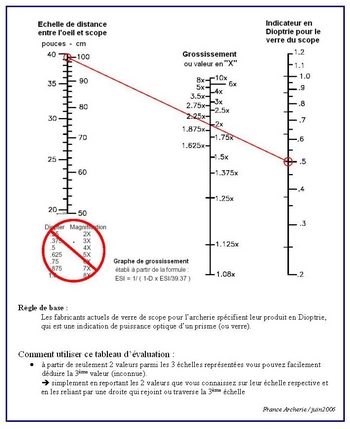
L’’usage des abaques telles que celles en ligne sur des sites Web comme celle-ci
sont utiles mais attention à ne pas utiliser les formules mal écrite (ça était d’ailleurs la motivation pour écrire cet article).
Il est préférable de soit prendre sa calculette et de se référer à la formule (3), soit utilisé le tableur fourni en document joint.

Il suffit de donner les diverses distances (celle de la cible laissée à 1000 m sauf si vous la connaissez et voulez avoir un résultat au pourcent prés...) pour connaître le grossissement du scope dans les conditions d’utilisations réelles.
Enfin pour ceux qui aiment bien les représentations graphiques, voici 4 courbes du grossissement (en ordonnée verticale) en fonction de la distance oeil-scope (en abscisse horizontale). Les 4 courbes correspondent à 4 lentilles différentes de dioptrie (0,25-0,50-0,75-1,00) que l’on peut trouver typiquement dans les magasins d’archerie.
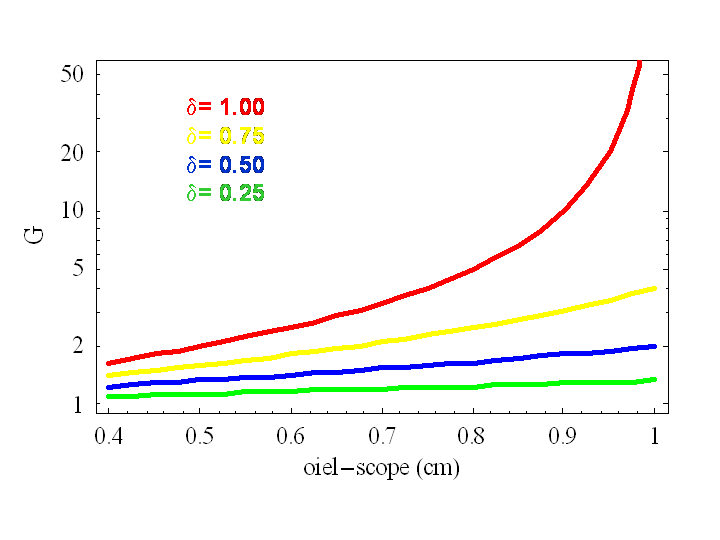
Courbes de grossissement
|
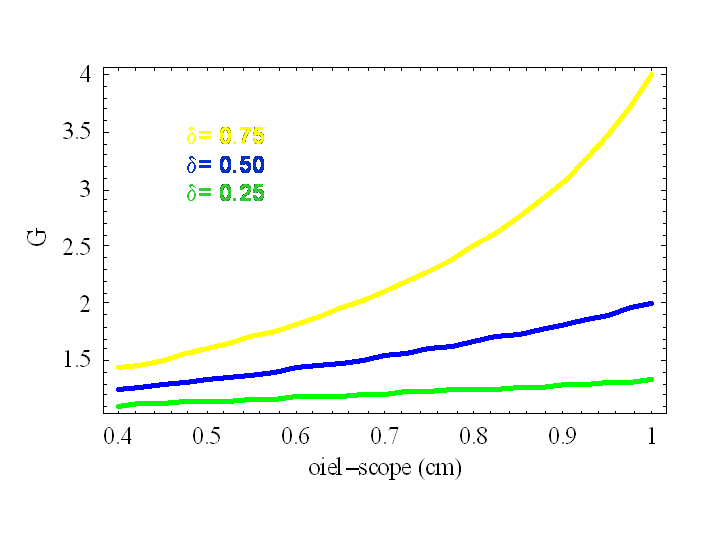
Courbes de grossissement
|
Résumé et perspectives
Dans cet article, nous avons jeté les bases de l’optique géométrique simple afin de pouvoir être en mesure de comprendre la formation de l’image d’une cible par la lentille du scope et d’en donner le grossissement. Ce dernier n’est pas un chiffre unique, il est fonction de non seulement de la dioptrie de la lentille mais également de la distance du scope à l’oeil de l’archer.
Dans des articles prochains, nous introduirons les autres éléments du système optique scope-visette-[lunette]-œil.
Compléments
A la lecture de ces quelques lignes, certain(e)s auront pu être choqué(e)s par le Vision de l’image AB : oeil nu ou avec scope. En effet, il semble que dans le cas de l’oeil nu, l’image soit vue dans un sens alors que lorsqu’on utilise le scope l’image soit renversée ! Il n’en est rien mais pour les besoins de la cause on ne peut pas représenter le phénomène en respectant les distances relatives : la distance cible est de l’odre de 10 m au moins, la distance focale (l’inverse de la vergence en dioptrie) de la lentille est de l’ordre du mètre, la dimension du scope de l’ordre de 2 à 3 cm et l’oeil a lui même des dimensions de l’ordre du cm...
Bon, et alors me direz-vous ! Voilà voilà, nous allons procéder en deux temps. D’abord considérons l’oeil nu. Si on reprend le schéma qui montre la Formation de l’image d’une lentille convergente, on remarque en effet que l’image d’un objet par une lentille convergente est renversée. Donc dans le cas de l’oeil nu, l’image sur la rétine sera renversée.
Complétons à présent la formation par l’oeil de l’image donnée par le scope.
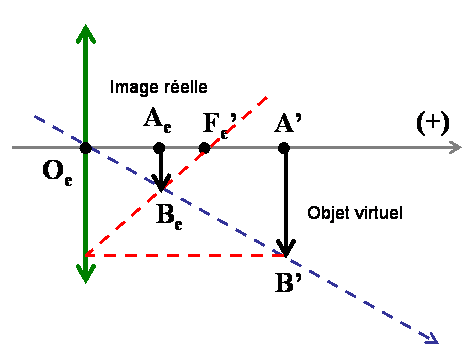
Etant donné que la distance focale de la lentille du scope est au moins de 1 m, l’image A’B’ de la cible donnée par le scope se trouve derrière l’oeil de l’archer (cf. formule 2). Mais il n’est pas nécessaire de vous retounez pour viser juste ! En effet, si on considère maintenant le cristallin de l’oeil, il peut être modélisé par une lentille convergente de centre $O_{e}$ et le foyer $F^{’}_{e}$ est situé à une distance de 1,5cm grosso-modo de $O_{e}$.
L’image A’B’ devient pour l’oeil l’objet dont il faut obtenir l’image $A_{e}B_{e}$(vous me suivez ?). Mais, attention cette fois, l’objet A’B’ est du même coté de $F^{’}_{e}$, et ça change tout ! On dit que cet objet est virtuel, et oui pincez vous peut-être êtes vous en train de rêver...
Si on reprend la formule 1 alors :
$$ \frac{1}{\overline{0_{e}A’}} - \frac{1}{\overline{0_{e}A_{e}}} = - \frac{1}{\overline{0_{e}F’_{e}}} $$
avec cette fois $\overline{0_{e}A’}>0$ et donc l’image est également située dans la même région de l’espace à droite du cristallin car alors
$$ \frac{1}{\overline{0_{e}A’}} = \frac{1}{\overline{0_{e}A_{e}}} + \frac{1}{\overline{0_{e}F’_{e}}} > 0 \quad \mathrm{donne} \quad \overline{0_{e}A’} > 0 $$
La construction est indiquée sur le schéma en prenant soin de prendre le foyer dit image $F^{’}_{e}$ pour construire la dite image et non le foyer objet qui n’est pas représenté mais qui satisferait $\overline{0_{e}F_{e}} = - \overline{0_{e}F’_{e}}$ (ou en d’autres termes, il se situe à gauche du cristallin à la même distance).
Donc, partant d’un objet AB dans un sens, l’image par le scope est inversée, et celle donnée $A_{e}B_{e}$ par l’œil garde cette inversion.
Ainsi que cela soit la cible vue à l’oeil nu, ou bien vue à travers le scope, au niveau de la rétine, l’image est dans le même sens (inversée), et notre cerveau fait le même traitement dans les deux cas. Donc tout va bien madame la marquise...