Introduction

Pour confectionner ses flèches, il faut se pencher sur la position du centre de gravité le long du tube, pointe et autres accessoires inclus. Dans le jargon, on parle alors du F.O.C de la flèche : Front Of Cernter.

Schéma

En naviguant sur le web on peut facilement trouver une figure de ce type

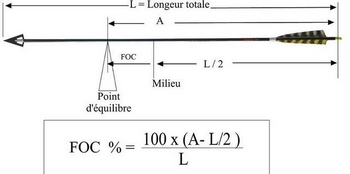
Où sont notées :

• L la longueur de la flèche pointe comprise et en partant du creux de l’encoche
• A la position du centre de gravité à partir du creux de l’encoche également.

Le calcul du F.O.C (en %) correspond en fait à la distance entre la position du centre de gravité et le milieu géométrique de la flèche.

La mesure

La mesure de la longueur totale de la flèche ne pose pas de problème. Celle de la position du centre de gravité peut se faire en posant une flèche finie sur un point d’appui rond (bout de tube) ou bien un profil en forme de ’L’, et à avancer la flèche jusqu’au moment où celle-ci bascule.

L’erreur de mesure du F.O.C (F) venant de l’erreur sur la détermination de A est égale à

$$ \frac{\Delta F}{F} = \left( 1 + \frac{1}{2 F} \left) \frac{\Delta A}{A} $$

Donc par exemple, si l’on fait une erreur de 1 cm sur la détermination de A d’une flèche ayant 68 cm de longueur et un FOC de 15% alors l’erreur relative sur A est de l’ordre de 1,5% et celle sur F de 6,5%. Donc on aurait F = 0,150 \pm 0,010 . La détermination est largement précise vous en conviendrez !!!

Prédiction

Ceci dit c’est bien joli de déterminer le FOC des flèches toutes faites mais il serait intéressant de pouvoir en déterminer la valeur grossièrement avant d’aller acheter son matériel, et en particulier ses pointes !

Pour cela on va simplifier le problème en prenant :

• un tube uniforme dans sa valeur de masse par unité de longueur selon toute sa longueur
• une pointe modélisée par un petit segment quasi-ponctuel en bout de flèche
• l’encoche et les empennages modélisés par une masselotte en bout de flèche

Alors le barycentre de entre le centre de gravité du tube de masse m, celui de la pointe de masse Met celui de la partie encoche-empennages de masse $\mathbf{\epsilon}$ est positionné tel que

$$ (M + m + \epsilon)\times A = M \times L + m \frac{L}{2} $$

Donc

$$ F = \frac{1}{2} \left( \frac{M}{M+m} \right)\left( \frac{1-\epsilon/M}{1+\epsilon/(M+m)} \right) \quad\quad Eq.1 $$

Maintenant, si l’on veut déterminer la masse de la pointe M pour un FOC donné (ex. 10% ou 15%) alors

$$ \boxed{ M = \frac{2Fm + (1+2F)\epsilon}{1-2F} = \frac{2F L \rho +(1+2F)\epsilon}{1-2F} } $$

où j’ai introduit la masse par unité de longueur $\rho$ qui est donné dans les tableaux Easton ou bien le logiciel du même fabricant.

Par exemple, pour des ACE 670 $\rho = 6$ grain/inche , pour une flèche de $L =$67,5cm = 26,6inches ayant un FOC final de 16% et une masse d’encoche-empennage de 14,5 grains (ex. 5,5 grains pour l’encoche et 3 grains par petit empennage de type "aileron de requin", mesures faites à la balance), alors la pointe doit avoir une masse de

$$ M = 100,8 \mathrm{grains} $$

Ce qui est remarquablement en accord avec les mesures d’une flèche toute montée où l’on trouve une masse de 100 grains un FOC de 15,7% !

Remarques finales

Donc dans ce bref article, on a introduit la notion de F.O.C d’une flèche, comment le mesurer en pratique, et comment dimensionner les éléments de la flèche avant montage pour obtenir un F.O.C donné.

Maintenant avant de clôre, il faut dire que la valeur ad equat du F.O.C reste une affaire de "tuning". Ce qui est courant de dire est qu’un F.O.C de 10% à 15% est de bon ton pour le tir FITA... A vos flèches !

Extras

Si on charge la pointe d’une masselotte
$\Delta m$ alors le F.O.C varie de la quantité

$$ \Delta F = (1/2 - F)\left( \frac{\Delta m}{m + \Delta m} \right) $$

Par exemple pour une flèche de 475 grains qui a un FOC de 5%, il suffit de lui adjoindre une masselotte de 20 grains pour obtenir un FOC de 7%.

Une autre façon d’écrire Eq.1 :

$$ F = \frac{1}{2} \left( \frac{m_p-m_e}{m_p+m_t+me} \right) $$

• $m_p$ : masse de la pointe
• $m_t$ : masse du tube seul donné par $\mu \times L_{nu}$ soit le produit de la masse par unité de longueur fois la longueur du tube nu ($\mu$ est souvent un des paramètres donnés par les constructeurs)
• $m_e$ : la masse totale coté encoche regroupant : encoche, bushing, wrap et empennages.

On voit bien avec cette expression comment évolue le FOC quand on change telle ou telle masse (ex. pointe, plumes...) et aussi la longueur du tube.