Introduction

Dans les articles L’optique du Pr. Lorgnon et Grossissement des scopes, je me suis attaché à donner les bases de calcul des grossissements des scopes ainsi qu’à donner les nomenclatures commerciales (non universelles !) de la "puissance" des lentilles. Dans cet article je vais m’intéresser à l’image que l’on a de la cible même si ce sujet ne peut être traité qu’avec des approximations car la vision de chacun est différente.

On a vu (si je puis dire) un peu d’optique en utilisant une méthode simple lors de l’établissement du facteur de grossissement de la lentille d’un scope d’arc à poulies. Dans cet article je vais utiliser une autre méthode développée également dans le cadre de l’optique géométrique proche de l’axe de symétrie des lentilles (ou de dioptres en toute généralité) basé sur le formalisme matriciel.

Formalisme matriciel pour l’optique

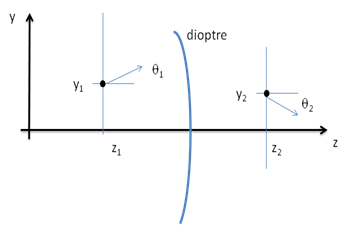
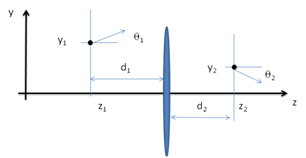
La figure 1 schématise le passage d’un rayon lumineux de la position 1 $(z_1,y_1)$ dirigé dans la direction $\theta_1$, à travers un dioptre (ex. une interface air-verre) de telle façon qu’il se retrouve à la position 2 $(z_2,y_2)$ allant dans la direction $\theta_2$. Dans le cas de l’optique proche de l’axe optique ($\sin \theta \simeq \theta$) alors une linéarisation des équations permet d’écrire une relation matricielle du type :

$$ \begin{pmatrix} y_2 \\ \theta_2 \end{pmatrix} = \begin{pmatrix} M_{11} & M_{12} \\ M_{21} & M_{22} \end{pmatrix} \begin{pmatrix} y_1 \\ \theta_1 \end{pmatrix} $$

Les coefficients $M_{ij}$ ci-après désignés par la lettre M dépendent du dioptre qui s’interpose entre les positions 1 et 2. Nous allons donner un certain nombre d’exemples.

Espace uniforme

Dans le cas où il n’y a pas de changement d’indice entre les deux positions 1 et 2, le rayon se propage en ligne droite et donc :

$$ \mathbf{M}_{uni}(d) = \begin{pmatrix} 1 & d \\ 0 & 1 \end{pmatrix} $$

avec $ d=z_2-z_1$.

Changement d’indice

Dans le cas du passage entre un milieu d’indice $n_1$ et un milieu d’indice $n_2$ (ex. passage air-eau où la paille semble cassée dans son verre de pastis…), juste à la transition il y a un changement de direction du rayon lumineux et

$$ \mathbf{M}(n_1,n_2) = \begin{pmatrix} 1 & 0 \\ 0 & n_1/n_2 \end{pmatrix} $$

Lentille mince

Si maintenant nous interposons une lentille mince alors on pourrait conjuguer les deux matrices déjà citées pour obtenir celle qui rend compte du fait que le rayon va changer de direction mais contrairement au cas du changement d’indice simple, ici le changement de direction dépend de la position par rapport à l’axe de la lentille. Sans démonstration, en fait le résultat se traduit par une matrice qui fait intervenir la focale de la lentille $f$ selon

$$ \mathbf{M}_{len}(f) = \begin{pmatrix} 1 & 0 \\ -1/f & 0 \end{pmatrix} $$

avec la convention de signe $f>0$ ($f<0$) pour une lentille convergente (divergente).

Image par de la cible par le scope

Considérons à présent le cas déjà rencontré dans l’article L’optique du Pr. Lorgnon de l’image de la cible à travers le scope de dioptrie $\delta=1/f$ (ici $f>0$). On procède en suivant le rayon depuis la position 1 à la position 2 pour identifier les matrices mises en jeu : de la position 1 à la lentille, le rayon lumineux ne subit pas de changement d’indice sur une distance $d_1$ donc on applique la matrice $\mathbf{M}_{uni}(d1) $, puis le rayon lumineux subit la traversée de la lentille modélisée par la matrice $\mathbf{M}_{len}(f) $, enfin de la lentille à la position 2 de nouveau le rayon lumineux n’est pas dévié et cela est traduit par l’utilisation de la $\mathbf{M}_{uni}(d2) $. Le point subtil et que l’on désire une relation donnant $( y_2,\theta_2)$ en fonction de $( y_1,\theta_1)$ donc mathématiquement il faut faire intervenir le produit des matrices mentionnées dans l’ordre inverse de la direction du rayon lumineux, ainsi il vient :

$$ \begin{pmatrix} y_2 \\ \theta_2 \end{pmatrix} = \begin{pmatrix} 1 & d_2 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ -1/f & 1 \end{pmatrix} \begin{pmatrix} 1 & d_1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} y_1 \\ \theta_1 \end{pmatrix} $$

Un peu de calcul donne l’expression de $y_2$ et $\theta_2$

$$ \begin{align*} y_2 &= y_1 \left(1-\frac{d_2}{f}\right) + \theta_1 d_1 d_2 \left( \frac{1}{d_1} + \frac{1}{d_2} - \frac{1}{f}\right) \\ \theta_2 &= \theta_1\left(1-\frac{d_1}{f}\right) - \frac{y_1}{f} \end{align*} $$

Comment obtient-on une image de la cible ? Prenons la croix du 10, son image est la localisation du point (valeur de $y_2$) dans le plan $z=z_2$ tels que tous les rayons lumineux émanant de cette croix (c’est-à-dire quelque soit $\theta_1$) convergent vers ce point image. Donc, l’image $y_1$ de la cible plus généralement est le lieu $y_2$ indépendant de $\theta_1$. Cette condition implique que le coefficient de $\theta_1$ dans l’expression de $y_2$ soit nul, d’où la condition de formation de l’image :

$$ \frac{1}{d_1} + \frac{1}{d_2} = \frac{1}{f} $$

Si on note O le centre de la lentille mince, A la position de la cible sur l’axe optique, A’ la position de l’image, F’ le foyer image alors on retrouve la formule algébrique de l’article L’optique du Pr. Lorgnon (le sens + est donné par l’orientation de l’axe z) :

$$ -* \frac{1}{\bar{OA}} + \frac{1}{\bar{OA’}} = \frac{1}{\bar{OF’}} $$

Le grossissement du scope peut également être retrouvé facilement

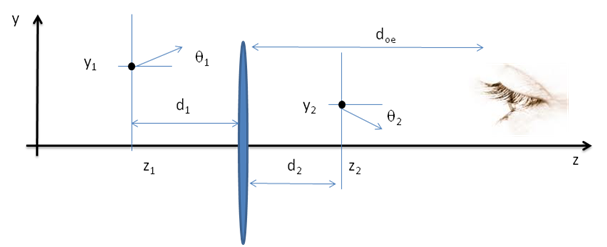
Si on enlève la lentille la cible est vue sous un angle

$$ \theta_{nu} = \frac{y_1}{d_1+d_{oe}} $$

tandis qu’à travers la lentille l’image est vue sous l’angle

$$ \theta_{sc} = \frac{-y_2}{d_{oe}-d_2} $$

(on prend $-y_2$ pour obtenir une valeur positive).
Donc le grossissement angulaire étant le rapport des deux quantités est égal à

$$ G_{sc} \equiv \frac{\theta_{sc}}{\theta_{nu}} = \frac{1}{\left(1-\frac{d_{oe}}{D}\right)\frac{d_{oe}}{f}-1} $$

Où j’ai posé $D=d_1+d_{oe}$ la distance de la cible à l’œil qui se rapproche d’ailleurs au mieux de la distance de tir (18m,…,90m).
Un petit rappel concernant le grossissement du scope : la formule ci-dessus indique comme nous l’avions vu L’optique du Pr. Lorgnon qu’il dépend à la fois de la focale $f$ (ou dioptrie $\delta$) ET de la distance de l’œil au scope ET de la distance à la cible !!!

En photo

Sur l’image ci-dessous, j’ai pris 3 photos d’un blason de tri-spots (20cm de diam.) prises à travers un scope de 35mm de diamètre muni d’un verre de 0.7 dioptrie posé à 15m de la cible. Les photos sont prises à 3 distances du scope (de gauche à droite) : 85cm, 160cm, 250cm. La première distance est celle que j’ai sur mon arc, la seconde distance montre que l’image est totalement floue avec une impression de ne voir que du jaune/orangé, sur la troisième on retrouve une image assez nette (inversée en fait mais pour un blason circulaire ça ne se remarque pas).

distance de "flou total"

Bon, le plus gênant est de se retrouver dans la situation de "flou total". Elle est due au fait qu’on place son oeil à l’endroit précis de la formation de l’image par la lentille du scope à cet endroit précis le grossissement angulaire présente une singularité :

$$ d_{soe}^{flou} = \frac{D}{2}\left\{1- \left( 1- \frac{4}{D \delta_{sco}} \right)^{1/2} \right\} $$

(nb. j’ai précisé la notation $d_{soe}$ pour la distance scope-oeil et $\delta_{sco}$ pour la dioptrie de la lentille du scope).

On peut illustrer l’évolution de cette distance (scope-oeil) en fonction de la dioptrie de la lentille du scope (abscisse) et pour différente distance à la cible (en bleu : 18m) :

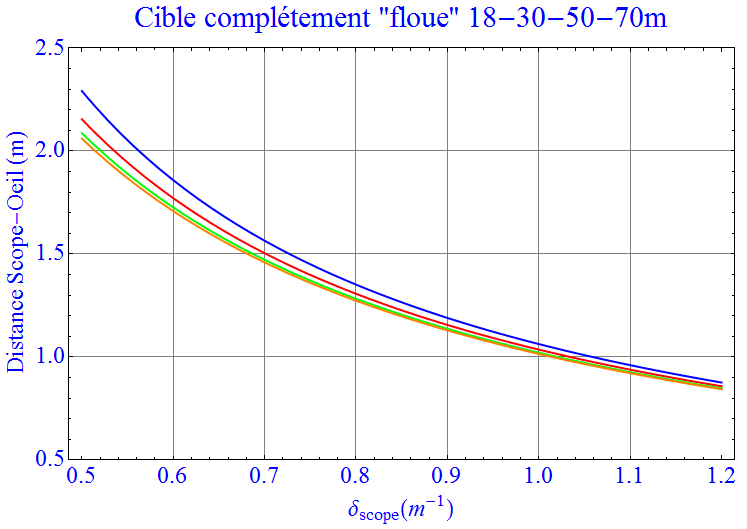
Avec 0.7 dioptrie la courbe bleu indique une distance de 1,60m ce qui confirme numériquement l’impression de la photo centrale vue plus haut. On remarque aussi qu’au delà de dioptries de lentille de 1, cette distance de flou est sensiblement égale aux distances oeil-scope typiques. A ces très forts grossissement il va falloir ruser ! Mais avant cela voyons la part du blason que l’on voit dans le scope.

Partie du blason vue dans le scope

Pour estimer la partie du blason que l’on voit dans le scope on peut se dire que l’angle sous lequel est vu l’image du blason à travers le scope est égal à l’angle sous lequel est vu le scope lui-même. Soit

$$ G_{scope} \theta_{nu} = \theta_{scope} $$

donne

$$ \emptyset_{blason} = \frac{D \emptyset_{scope}}{d_{soe} G_{scope}} $$

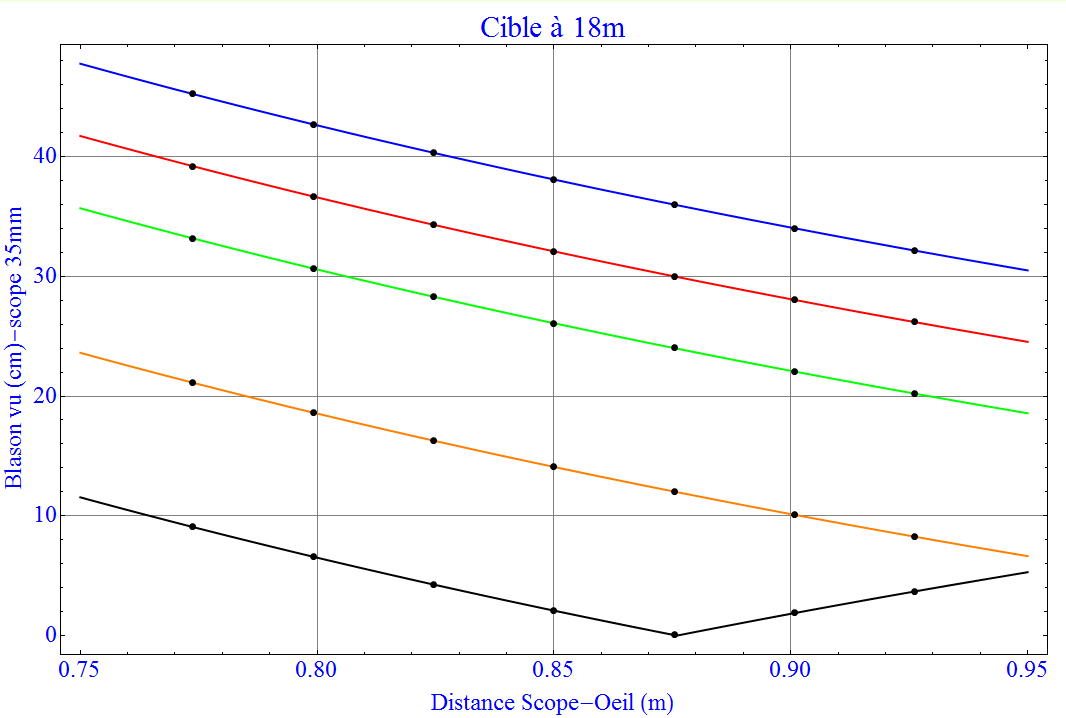
Sur l’image ci-dessous j’ai présenté le diamètre vu (en cm) à travers un scope de 35mm de diamètre placé à une distance de l’oeil entre 75cm et 95cm et pour différentes dioptries de lentille de scope : 0.6 (bleu), 0.7 (rouge), 0.8 (vert), 1.0 (orange), 1.2 (noir).

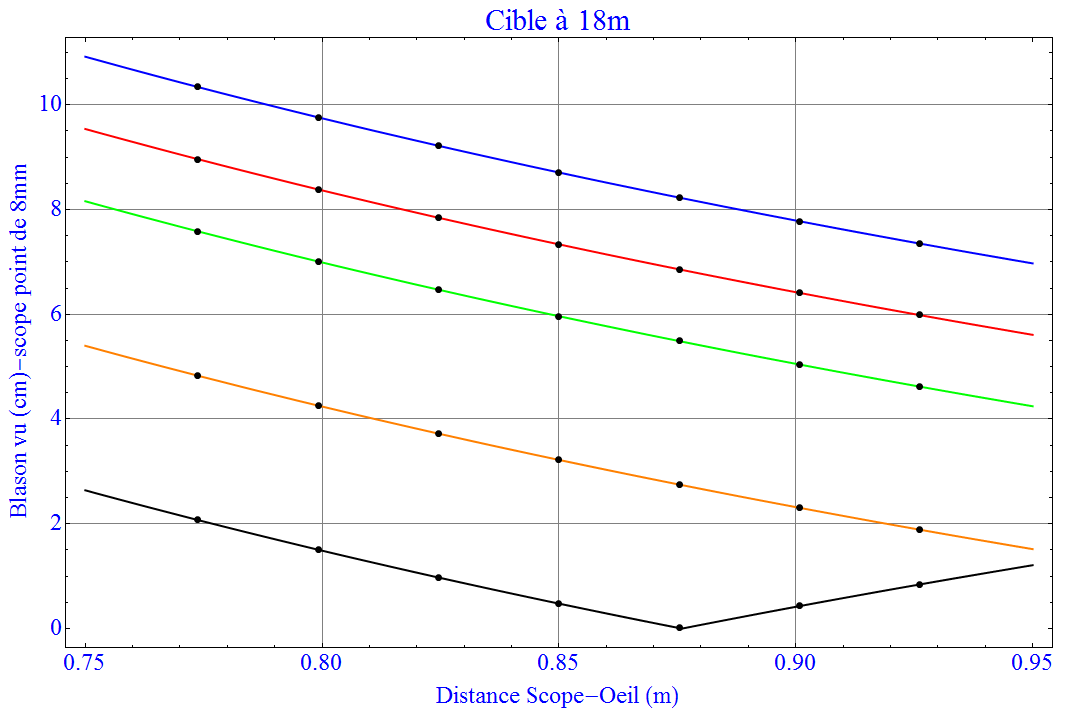
On peut remarquer qu’avec ma dioptrie de 0.7 et mon scope à 85cm je vois largement tout le blason de 20cm de diamètre , et certain vont chercher à augmenter le grossissement et hésiter à passer à des valeurs de dioptrie de 0.8 et 1.0 (il n’y a pas de 0.9 sauf preuve du contraire). Bon çà c’est un calcul possible. Mais il y en a un autre : prenons un point de visée de 8mm de diamètre, certes gros mais sur un scope de 35mm la fraction de surface n’est que de 6%, alors que cache-t’on ? La réponse dans l’image ci-dessous

Dans ma configuration (mon scope à 85cm, lentille de 0.7 courbe rouge) je cache quasiment tout le jaune ! C’est ce que je veux : je vois tout le blason largement pour ne pas me tromper de cible et je cache tout le jaune pour moins de stress en visée. Encore une fois c’est mon choix actuel. J’aurai au moins donné à tout à chacun les éléments pour faire son choix en toute connaissance de causes.

Remarquons que sur les deux images ci-dessus, la courbe noir (dioptrie de 1.2) il y a une réflexion pour environ 88cm. Cela n’est pas étonnant car c’est là où le grossissement est "infini", on dilate complètement l’image du blason. C’est la région du "flou" mentionné plus haut.

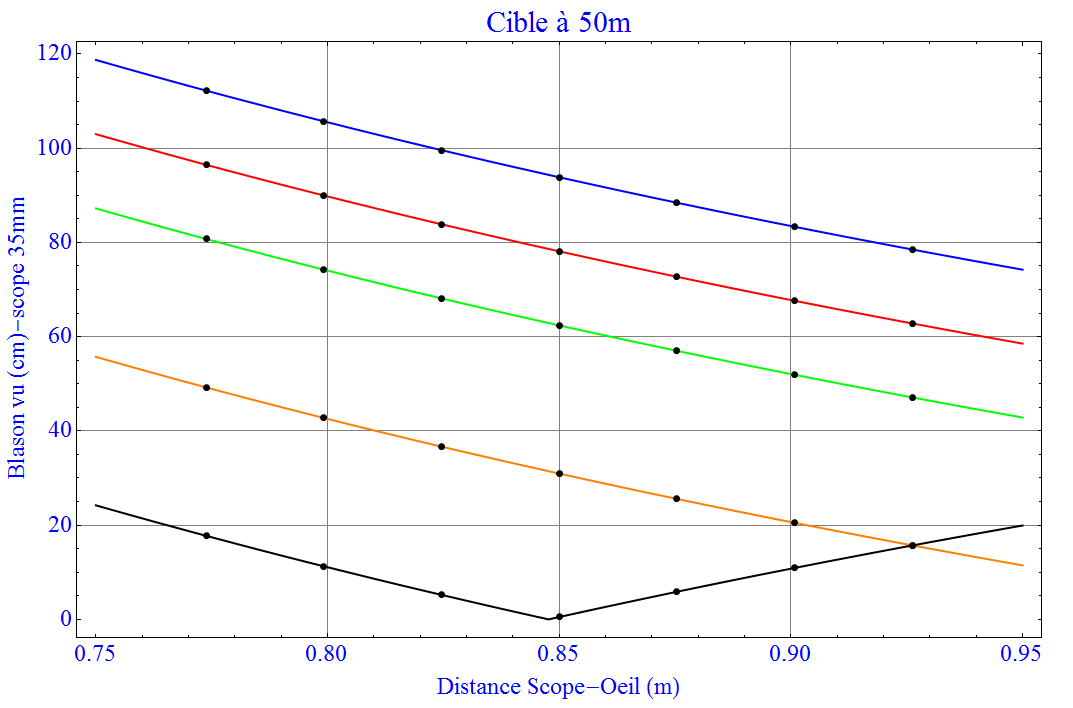
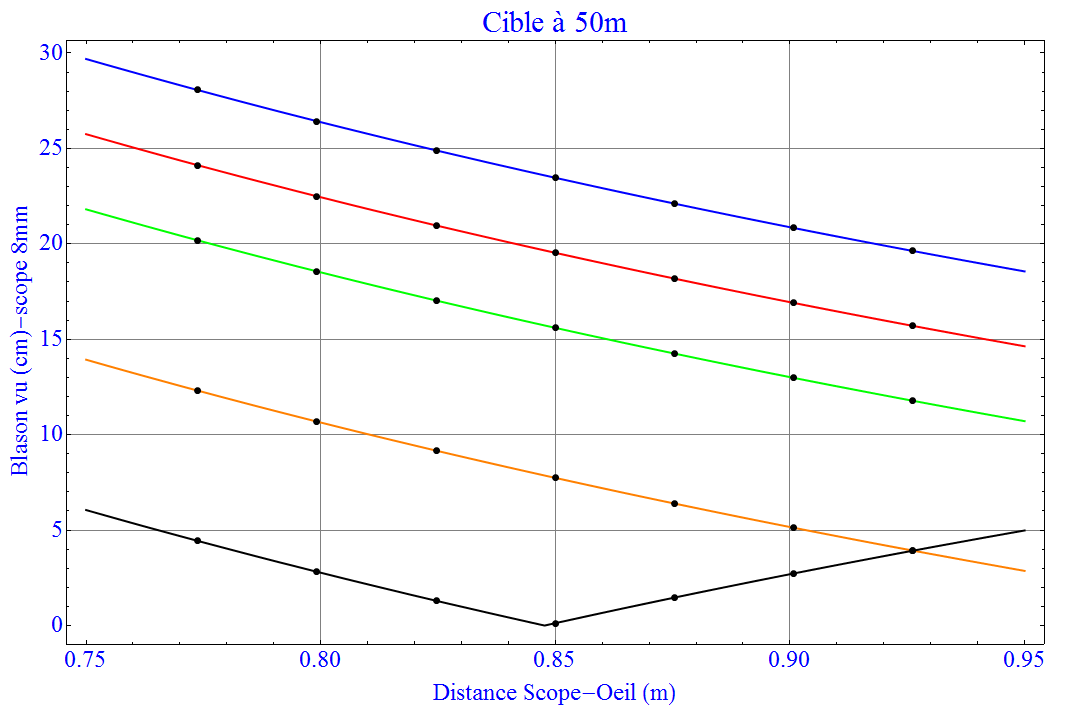
En passant à 50m que se passe-t’il avec le même scope de 35mm de diamètre ?

Je vois toujours bien mon blason qui a un diamètre de 48cm. Et mon point de visée de 8mm me cache 19cm ce qui est plus grand que les 16cm du jaune. Je devrai peut-être changer non pas ma lentille (ça coûte cher !) mais mon point de visée pour passer à un 6mm.

Une dernière chose avant de voir ce qu’il se passe au niveau de la rétine, quand on grossit l’image, il est bon de rappeler que la luminosité diminue ! Et oui à éclairement égal du blason, un plus gros grossissement voit une fraction de blason moindre comme on a vu plus haut, et donc la partie vue ne renvoie donc qu’une fraction de la totalité de la lumière d’éclairement... Pour éclaircir le blason, opter pour une distance de scope plus petite et//ou changer de lentille (dioptrie plus faible).

Focalisation sur la rétine

On va introduire une version simplifiée de l’oeil (voir Optique géométrique : Imagerie et instruments par Bernard Balland) : elle consiste en une lentille convergente de 60 (pour voir un objet à l’infini) à 65 dioptrie (pour voir un objet de près) située à 1.7cm de la rétine.

Sur le schéma suivant j’ai indiqué les variables pour fixer les idées :

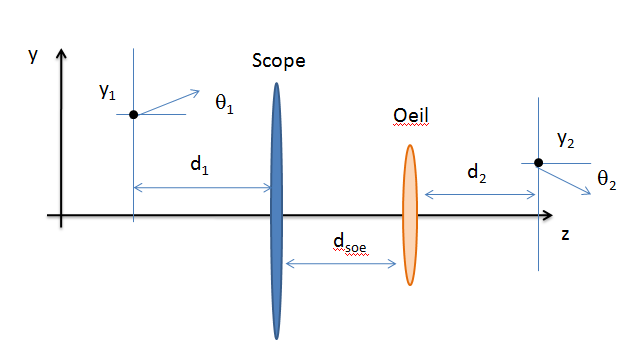
Le formalisme matriciel introduit au début de l’article va aider car il suffit de rajouter 2 matrices 2x2 par rapport à 1 lentille simple. Il vient

$$ \begin{align*} \begin{pmatrix} y_2 \\ \theta_2 \end{pmatrix} &= \begin{pmatrix}1 & d_2 \\ 0 & 1 \end{pmatrix} \begin{pmatrix}1 & 0 \\ -\delta_{oe} & 1 \end{pmatrix} \begin{pmatrix}1 & d_{soe} \\ 0 & 1 \end{pmatrix} \\ & \times \begin{pmatrix}1 & 0 \\ -\delta_{sco} & 1 \end{pmatrix} \begin{pmatrix}1 & d_1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} y_1 \\ \theta_1 \end{pmatrix} \end{align*} $$

où j’ai introduit la dioptrie du scope ($\delta_{sco}$) celle de l’oeil ($\delta_{oe}$) et la distance entre le scope et l’oeil ($d_{soe}$). Comme avant $d_1$ désigne la distance de la cible au scope ($d_1 = D-d_{soe}$) et $d_2$ la distance entre la lentille de l’oeil est l’image formée par le système des 2 lentilles. En partant du principe déjà utilisé que l’image se forme à un point $y_2$ indépendant de $\theta_1$. En négligeant les termes d’ordre $1/D^2$ et supérieur, on trouve alors

$$ \begin{align*} d_2 &= \frac{1 - d_{soe}*\delta_{sco}}{\delta_{oe} + \delta_{sco} -* d_{soe}\delta_{oe}\delta_{sco}} \\ &+\frac{1}{D*(\delta_{oe} \delta_{sco} - d_{soe}\delta_{oe} \delta_{sco})^2} + \dots \end{align*} $$

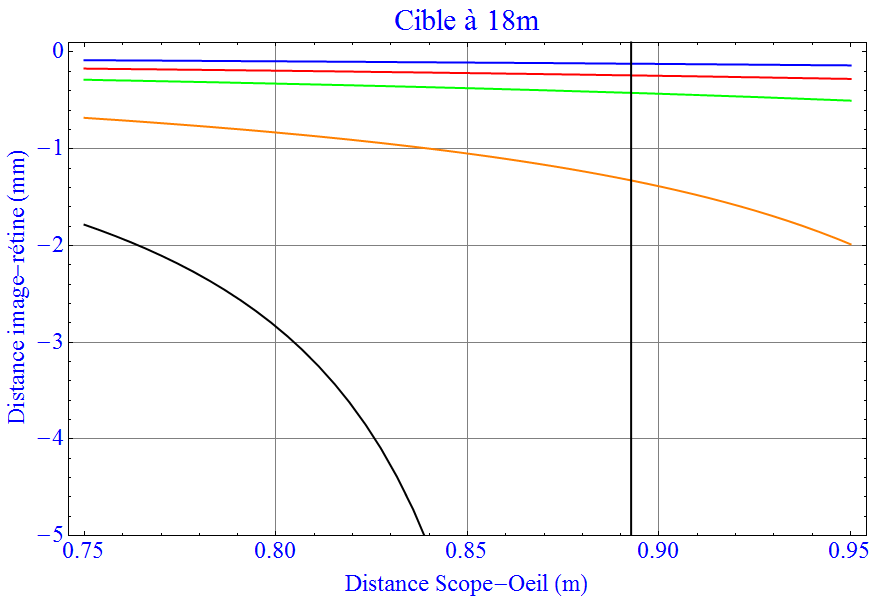
Dans l’image suivante j’ai comparé cette distance à celle entre la lentille de 60 dioptries modélisant le cristallin au repos et la rétine (attention l’échelle verticale est en millimètre) :

Le code de couleur est toujours le même : bleu (0.6 dioptrie), rouge (0.7 dioptrie), vert (0.8 dioptrie), orange (1.0 dioptrie) et noir (1.2 dioptrie). On note que l’oeil accommode parfaitement une cible placée à 18m avec des scopes de puissance inférieure à 1.0 dioptrie et que pour une lentille de 1.2 dioptrie aucun oeil "normal" ne peut faire le point. Il y a la fameuse singularité du grossissement qui se voit (barre verticale). Il faut envisager d’inclure une visette correctrice mais cela fera l’objet d’un autre article (faut faire durer le suspense...).

Résumé

Dans cette article j’ai mis en place le formalisme matriciel de l’optique géométrique et je l’ai appliqué au cas simple du calcul du grossissement par un un scope simple. On en a déduit des relations permettant de trouver la fraction de blason vue et j’ai montré comment on peut s’en servir pour choisir ma puissance de son scope, la taille de son point de visée et la distance entre son oeil et le scope. Ensuite, le formalisme permet simplement d’introduire une modélisation de l’oeil qui permet de montrer où se focalise l’image du blason au niveau de la rétine. La nécessité d’utiliser des visettes correctrices est mise en évidence pour des puissances de scope très fortes ou des configurations où l’oeil est situé aux alentours de la zone de "flou" causé par la singularité du grandissement angulaire du scope. A suivre.