Introduction
Dans l’article Réglages viseurs en parcours : petites et grandes distances (à plat) j’ai (ré)étudié le réglage du viseur dans le cas où les cibles sont sur un plan horizontal. Nous avons vu la façon dont l’abaque qui donne le réglage à effectuer en fonction de la distance présente la particularité d’avoir une redondance entre petites et grandes distances. Cela tient au fait que la flèche se trouve en dessous de la ligne de visée.
Dans cet article, je vais exposer les modifications à apporter dans le cas où l’archer se trouve sur une pente ascendante ou descendante comme on peut le voir sur les photos ci-dessous.
Mise en place des équations et résolution
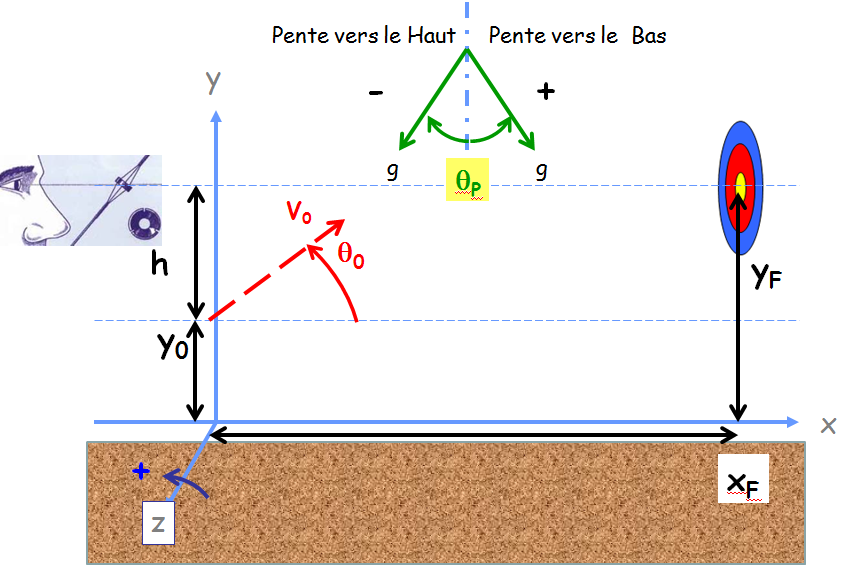
Sur la figure ci-dessous j’ai mis en scène un archer visant une cible qui se trouve sur une pente ascendante.
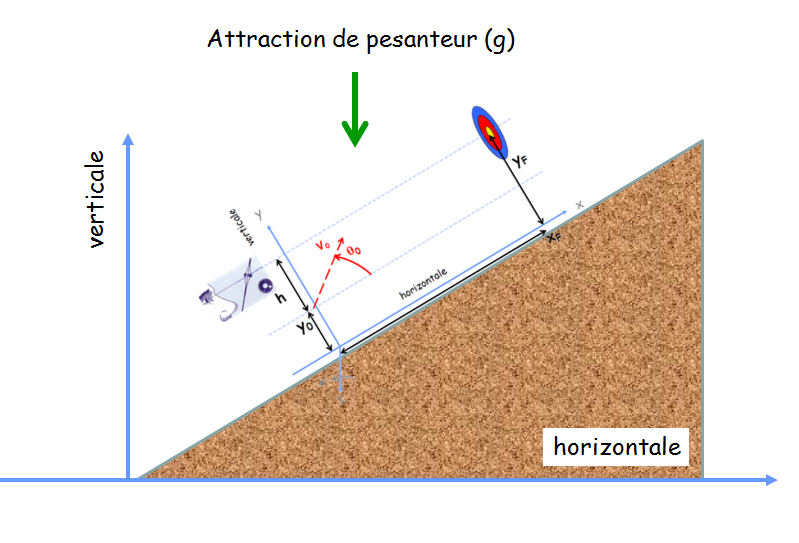
Remarquez que la direction de l’attraction terrestre (g) est toujours verticale donnée par exemple par un fil à plomb, mais ne correspond plus à la verticale vue dans le repère « local » de l’archer que j’ai introduit dans Réglages viseurs en parcours : petites et grandes distances (à plat).
La figure suivante présente ce qu’il se passe dans ce repère local.
Remarquez cette fois la direction de l’attraction terrestre (g) qui change selon la direction et l’angle ( $\theta_p$ ) de la pente. Si la pente est montante alors $\theta_p$ est pris négatif et l’inverse pour une pente descendante.
Une fois le repère fixé, on peut suivre la démarche de l’article Dynamique d’une fléche en phase de vol (Partie I) par exemple. Les équations d’évolution temporelle d’un point matériel $(X(t), Y(t))$ dans ce champ de pesanteur sont données par la loi de Newton entre force et accélération (rappel : la masse disparaît naturellement des équations). Il vient [1] :
$$ \begin{align*} \ddot{X}(t) & = g \sin\theta_p \\ \ddot{Y}(t) & = - g \cos\theta_p \end{align*} $$
L’intégration successive se fait de la même façon que pour l’article précité et l’on obtient pour un projectile lancé à $t=0$ depuis $(0,y_0)$ avec la vitesse $v_0$ avec un angle $\theta_0$ les équations suivantes :
$$ \begin{align*} X(t) & = v_0 \cos\theta_0 t + \frac{1}{2} g \sin\theta_p t^2\\ Y(t) & = y_0 + v_0 \sin\theta_0 t - \frac{1}{2} g \cos\theta_p t^2 \end{align*} $$
On reconnait au passage le cas où $\theta_p = 0$ où $X(t)$ évolue linéairement en fonction du temps et peut directement être transféré dans l’équation donnant $Y(t)$ pour donner l’équation parabolique familière. D’une manière générale, dans le repère local de l’archer, l’équation d’évolution n’est plus une parabole. Par contre pour un observateur lié au repère terrestre, la trajectoire est toujours parabolique.
L’objectif de l’archer est d’atteindre la cible en $(x_F, y_F)$ et rappelons que la flèche part sous la ligne de visée avec $h = y_F - y_0$. Le temps $t_F$ pour atteindre la cible est donné par [2] :
$$ t_F = \frac{ x_F \cos\theta_p + h \sin\theta_p }{v_0 \cos(\theta_0-\theta_p)} $$
Cette expression reportée dans l’équation d’évolution de $Y(t)$ donne après quelques manipulations trigonométriques une équation dont la variable est $\tan\theta_0$ notée ($t_0$) [3] :
$$ h - \frac{t_0}{1+t_0\tan\theta_p} (x_F-h\tan\theta_p) + \frac{\cos^3\theta_p}{2 x_F^{max}}(x_Fh\tan\theta_p)^2\left[1+\left(\frac{t_0 -\tan\theta_p}{1+t_0\tan\theta_p}\right)^2\right]=0 \quad (1) $$
Au passage pour $\theta_p = 0$ on obtient :
$$ h - t_0 x_F + \frac{x_F^2}{x_F^{max}} (1+t_0^2) = 0 $$
Qui est une expression conforme à celle trouvée dans l’article Réglages viseurs en parcours : petites et grandes distances (à plat).
Exemples
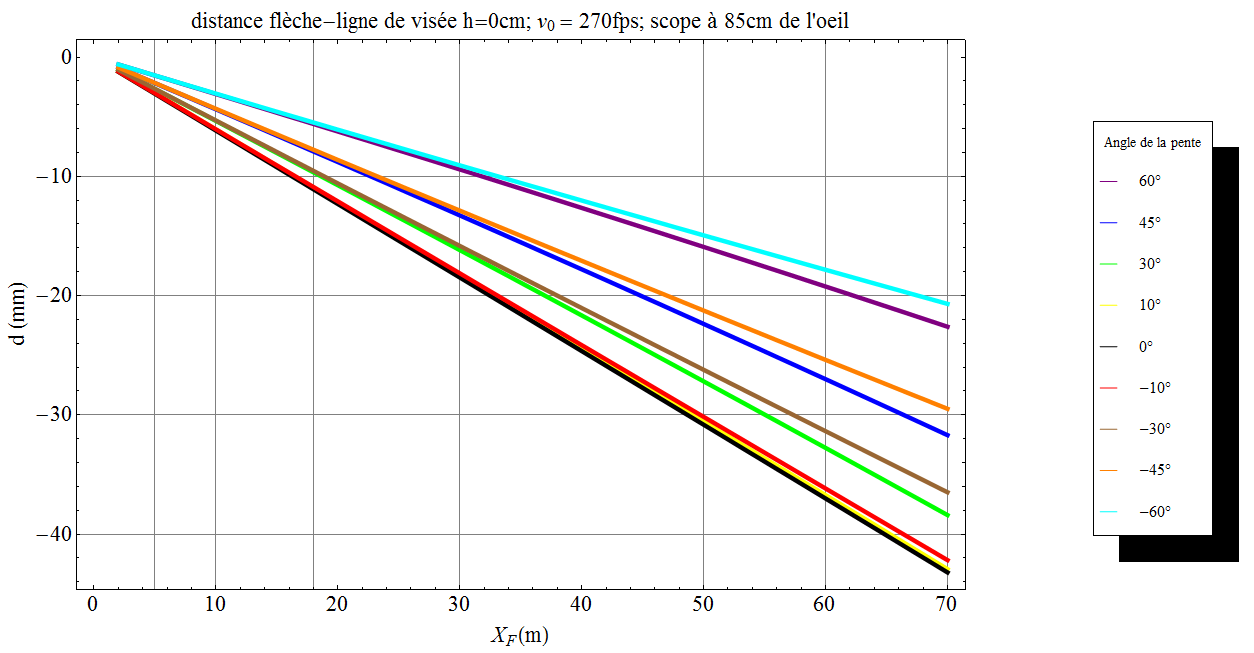
Tout d’abord, on peut examiner le cas où l’archer vise avec la flèche prés de son œil. Alors $h = 0$cm et l’on obtient :
En abscisse la distance à la cible, en ordonnée le réglage du viseur relatif par exemple à la cible à 5m. Le code des couleurs des différentes courbes correspond à la valeur de l’angle de la pente en degré (rappel les valeurs négatives correspondent par convention à une pente montante). Pour mémoire la courbe noire donne l’abaque sur terrain plat.
On constate :
- que l’on surestime la correction du viseur si l’on applique l’abaque ‘à plat’ dés lors que la pente dépasse les 10° ;
- les corrections pour les cas de terrains montants ou descendants sont quasi-identiques jusqu’à 40m (ici pour 270fps).
On retrouve bien des résultats vus dans l’article Dynamique d’une fléche en phase de vol (Partie II).
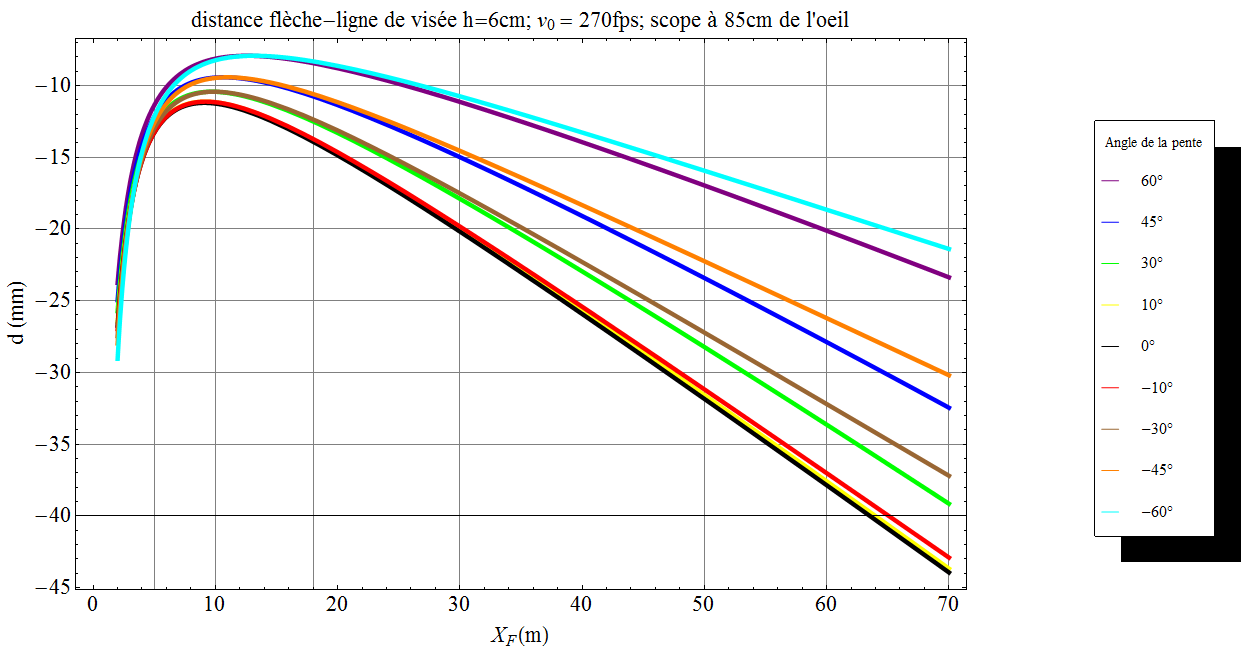
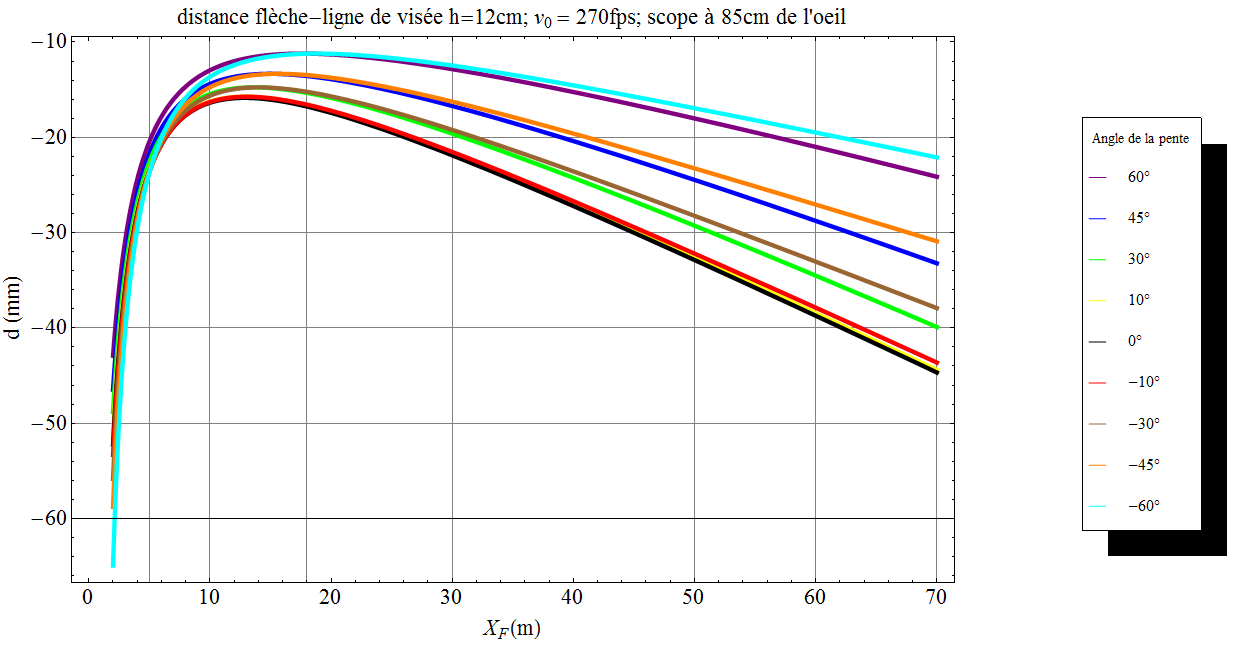
Maintenant, les deux graphes suivants donnent les mêmes courbes que précédemment mais pour les cas où la flèche se trouve sous la ligne de visée avec $h = 6cm$ et $h=12$cm.
On constate comme précédemment que :
- il y a surestimation de la correction dès lors qu’il y a une pente
- on retrouve le résultat de l’article Réglages viseurs en parcours : petites et grandes distances (à plat) à savoir qu’il y a une correspondance de réglage entre petites et grandes distances, mais que cette correspondance est modifiée à cause de la pente
- la différence de correction entre pente positive ou négative est d’autant moins importante que la flèche se trouve sous la ligne de visée.
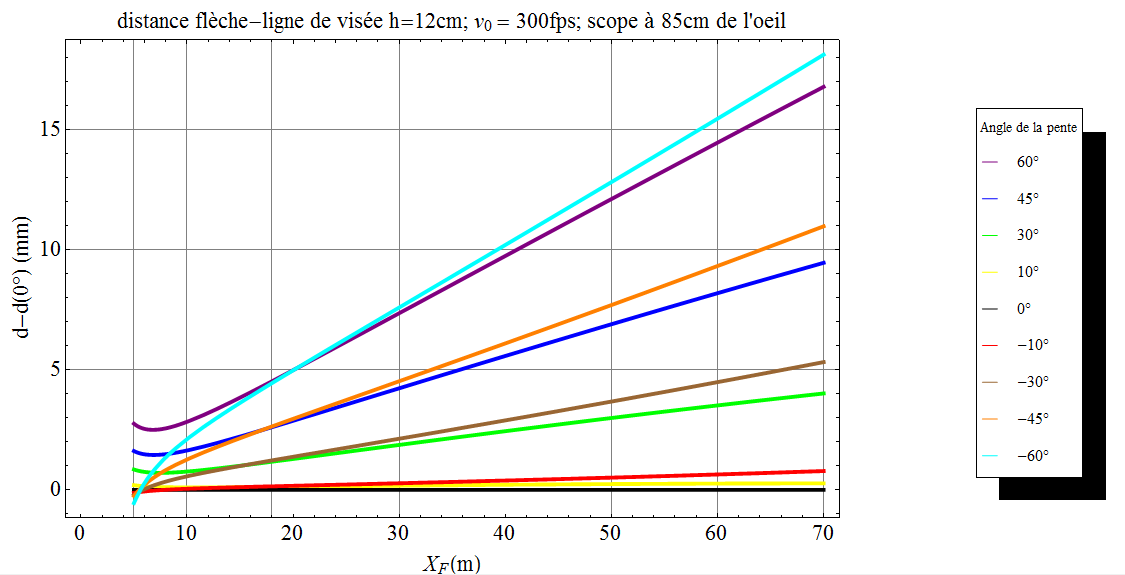
Finalement, voici la modification des courbes quand on passe à une vitesse initiale $v_0 = 300$fps.
A part un rétrécissement de l’abaque les constats précédents ne sont pas modifiés.
Rapport entre abaque à angle et celle sur le plat
Il peut être intéressant d’avoir en tête la façon dont se démarque une abaque pour un angle de pente donné et celle que l’on s’est constituée sur un sol horizontal. Voici un exemple :
On remarque qu’après 10m environ les corrections dues aux pentes sont linéaires ce qui peut permettre des moyens de constituer l’abaque sans la surcharger.
Conclusion
Dans cet article, j’ai pris en compte le décalage entre la ligne de visée et la position de la flèche à pleine allonge et j’ai introduit le paramètre de pente pour en déduire l’évolution de l’abaque. Cela généralise à la fois l’article Réglages viseurs en parcours : petites et grandes distances (à plat) et l’article Dynamique d’une fléche en phase de vol (Partie II). Encore une fois les valeurs numériques ne sont données qu’à titre indicatif, tout dépend de la vitesse d’éjection de l’arc, de la position du scope et de la façon dont l’archer position sa flèche à pleine allonge.
Epilogue
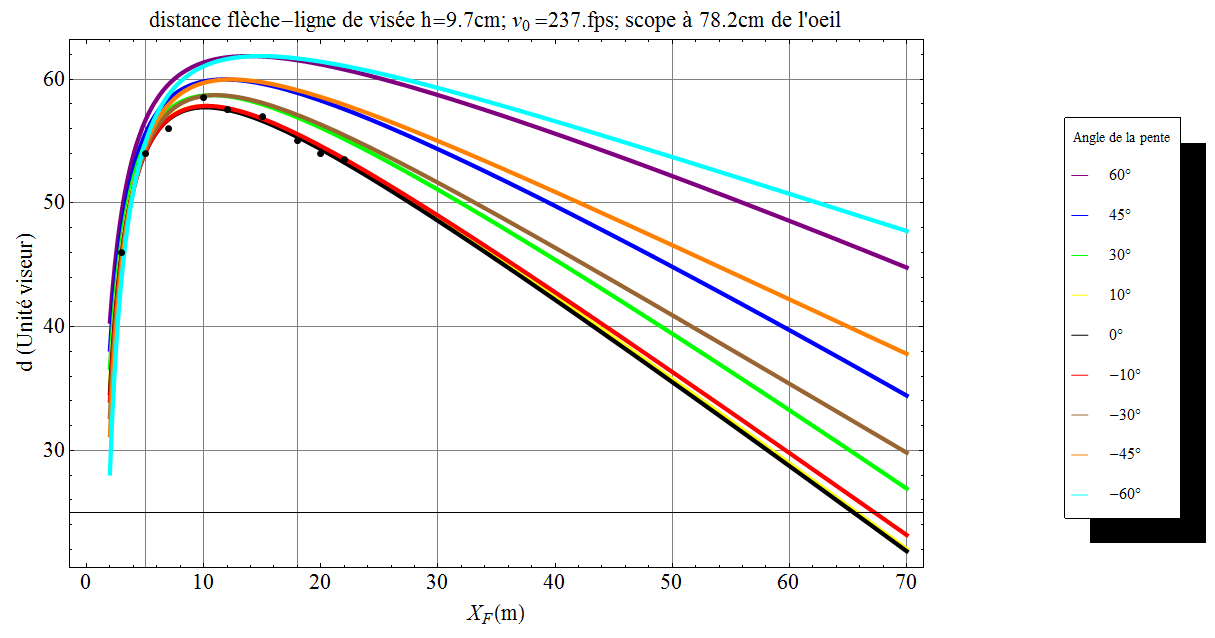
Ayant effectuer des réglages en salle par exemple entre 3m et 22m (points noir de la figure ci-dessous), on peut ajuster les paramètres vitesse de libération, distance oeil-viseur et distance oeil-encoche et en déduire alors les abaques à plat et en pente.
On peut le faire également sous forme de tablette avec une valeur tous les 5m et tous les 10° (montant)
| 0.0 | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | |
| 5.0 | 54.0 | 54.2 | 54.4 | 54.8 | 55.3 | 55.9 | 56.6 | 57.6 | 59.4 | 71.9 |
| 10.0 | 57.7 | 57.8 | 58.2 | 58.7 | 59.4 | 60.3 | 61.4 | 62.6 | 64.1 | 71.9 |
| 15.0 | 56.6 | 56.8 | 57.2 | 58.0 | 59.0 | 60.3 | 61.8 | 63.6 | 65.5 | 71.9 |
| 20.0 | 54.3 | 54.5 | 55.1 | 56.1 | 57.5 | 59.2 | 61.2 | 63.4 | 65.9 | 71.9 |
| 25.0 | 51.6 | 51.8 | 52.5 | 53.7 | 55.4 | 57.6 | 60.1 | 62.9 | 65.9 | 71.9 |
| 30.0 | 48.6 | 48.8 | 49.6 | 51.1 | 53.1 | 55.7 | 58.7 | 62.1 | 65.7 | 71.9 |
| 35.0 | 45.4 | 45.6 | 46.6 | 48.3 | 50.7 | 53.7 | 57.2 | 61.2 | 65.4 | 71.9 |
| 40.0 | 42.2 | 42.4 | 43.5 | 45.4 | 48.1 | 51.6 | 55.6 | 60.1 | 65.0 | 71.9 |
| 45.0 | 38.9 | 39.1 | 40.3 | 42.5 | 45.5 | 49.4 | 53.9 | 59.0 | 64.5 | 71.9 |
| 50.0 | 35.5 | 35.8 | 37.1 | 39.4 | 42.8 | 47.1 | 52.2 | 57.9 | 64.0 | 71.9 |
| 55.0 | 32.2 | 32.4 | 33.8 | 36.4 | 40.1 | 44.8 | 50.4 | 56.7 | 63.5 | 71.9 |
| 60.0 | 28.7 | 29.0 | 30.5 | 33.3 | 37.3 | 42.4 | 48.6 | 55.4 | 62.9 | 71.9 |
| 65.0 | 25.3 | 25.5 | 27.1 | 30.1 | 34.5 | 40.0 | 46.7 | 54.2 | 62.3 | 71.9 |
| 70.0 | 21.9 | 22.0 | 23.7 | 26.9 | 31.6 | 37.6 | 44.8 | 52.9 | 61.7 | 71.9 |
Idem pour les dévers :
| 0.0 | -10.0 | -20.0 | -30.0 | -40.0 | -50.0 | -60.0 | -70.0 | -80.0 | -90.0 | |
| 5.0 | 54.0 | 54.0 | 54.1 | 54.2 | 54.4 | 54.7 | 54.8 | 54.7 | 52.9 | 71.9 |
| 10.0 | 57.7 | 57.8 | 58.1 | 58.6 | 59.3 | 60.1 | 61.0 | 62.0 | 62.7 | 71.9 |
| 15.0 | 56.6 | 56.8 | 57.3 | 58.1 | 59.1 | 60.4 | 61.9 | 63.4 | 65.0 | 71.9 |
| 20.0 | 54.3 | 54.6 | 55.3 | 56.3 | 57.7 | 59.5 | 61.4 | 63.6 | 65.8 | 71.9 |
| 25.0 | 51.6 | 51.9 | 52.8 | 54.1 | 55.9 | 58.0 | 60.5 | 63.2 | 66.0 | 71.9 |
| 30.0 | 48.6 | 49.0 | 50.0 | 51.6 | 53.8 | 56.3 | 59.3 | 62.5 | 65.9 | 71.9 |
| 35.0 | 45.4 | 45.9 | 47.2 | 49.0 | 51.5 | 54.5 | 58.0 | 61.7 | 65.7 | 71.9 |
| 40.0 | 42.2 | 42.8 | 44.2 | 46.4 | 49.2 | 52.7 | 56.6 | 60.9 | 65.4 | 71.9 |
| 45.0 | 38.9 | 39.6 | 41.2 | 43.7 | 46.9 | 50.8 | 55.2 | 60.0 | 65.1 | 71.9 |
| 50.0 | 35.5 | 36.3 | 38.2 | 40.9 | 44.5 | 48.8 | 53.7 | 59.0 | 64.7 | 71.9 |
| 55.0 | 32.2 | 33.1 | 35.1 | 38.2 | 42.1 | 46.9 | 52.2 | 58.1 | 64.2 | 71.9 |
| 60.0 | 28.7 | 29.8 | 32.0 | 35.4 | 39.7 | 44.9 | 50.7 | 57.1 | 63.8 | 71.9 |
| 65.0 | 25.3 | 26.5 | 29.0 | 32.6 | 37.3 | 42.9 | 49.2 | 56.1 | 63.4 | 71.9 |
| 70.0 | 21.9 | 23.2 | 25.9 | 29.8 | 34.9 | 40.9 | 47.7 | 55.1 | 62.9 | 71.9 |
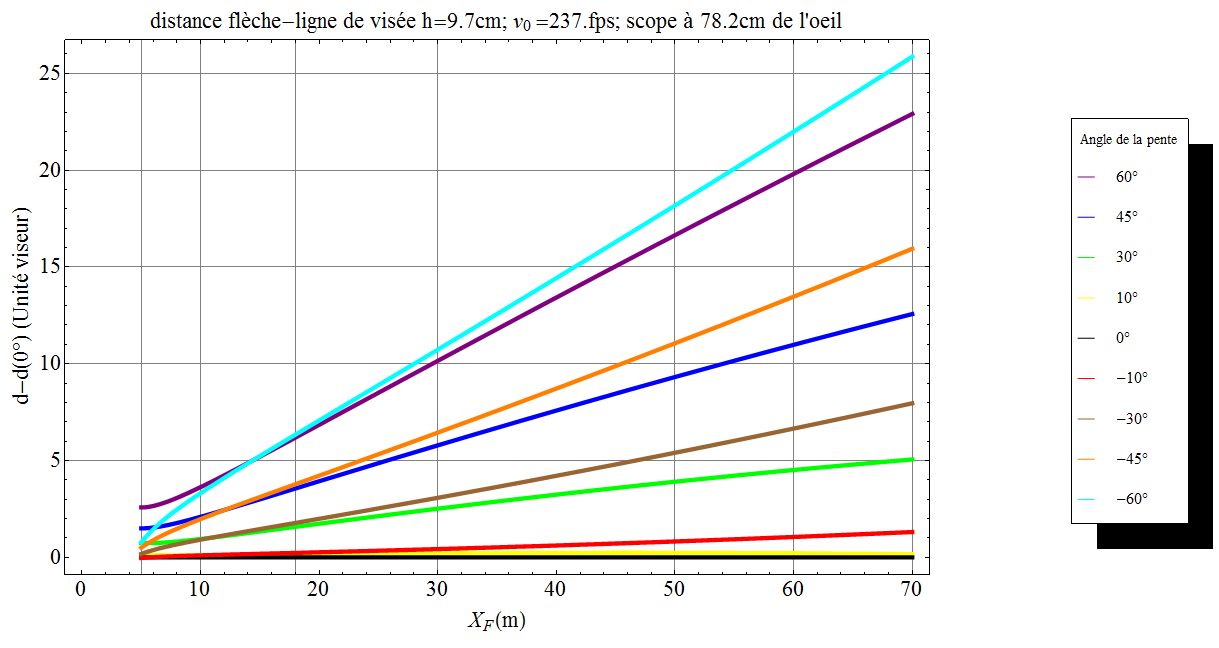
Et pour les différences entre réglages en pente et à plat cela donne
Bien entendu, il faut affiner et confirmer sur le terrain mais ça donne une idée assez précise de ce à quoi on doit s’attendre.