Introduction
Dans les articles Dynamique d’une fléche en phase de vol (Partie I) et Dynamique d’une fléche en phase de vol (Partie II), j’ai donné des indications sur le vol d’une flèche partant de l’arc $(0,y_0)$ pour arriver à la cible $(x_{F},y_{F})$ sans prendre en compte la ligne de visée.
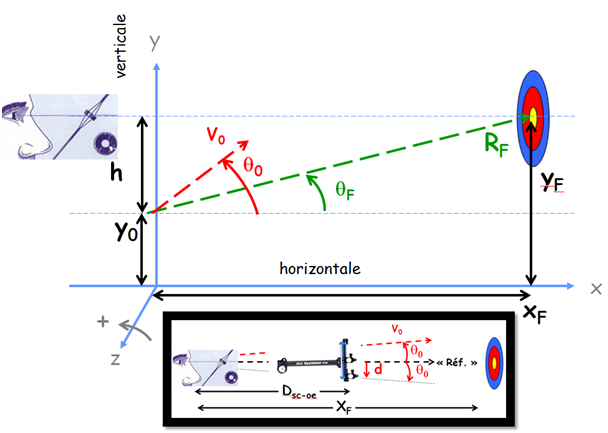
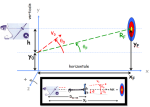
Sur la Figure 1, j’ai schématisé la position ($h$) de la flèche au niveau de la fenêtre d’arc. relativement à la position de l’œil visant la cible. A vitesse $v_0$ infinie, il est clair que la trajectoire étant une droite la flèche doit être telle que $\theta_0 = \theta_F$, et on a la relation
$$ \theta_F = \theta_{0,\infty} = \tan^{-1}\left( \frac{h}{x_F} \right) \approx \frac{h}{x_F} $$
(notons au passage $x_F = R_F \cos\theta_F$).
Or, nous savons que la vitesse de la flèche est loin d’être infinie et que la trajectoire est plus ou moins une parabole (exactement uniquement quand on néglige l’effet de l’air, voir Dynamique d’une flèche en phase de vol (partie III) et Dynamique d’une flèche en phase de vol (partie IV)). Donc la relation donnant $\theta_0$ va dépendre de $h$, $x_F$ et $v_0$. C’est le but de cet article.
Mise en équation du réglage du viseur
On va se servir d’un résultat de l’article Dynamique d’une fléche en phase de vol (Partie II) à savoir :
$$ \frac{\tan \theta_F}{\tan(\theta_0)} = 1 - \frac{x_F}{x_F^{max}\sin 2\theta_0} \quad(1) $$
Par rapport à l’équation (4) de l’article cité, j’ai utilisé (rappel) :
- la relation $\theta_0 = \theta_F+\alpha_0$ ;
- la définition de la portée maximale $x_F^{max} = v_0^2/g$ avec $g$ l’accélération de la pesanteur dont la valeur numérique est de l’ordre de $9.81m.s^{-2}$).
Ceci dit ce qu’il importe au bout du compte est le réglage vertical du viseur (encart dans la Figure 1). Comme montrer dans Dynamique d’une flèche en phase de vol (partie IV), il y a une relation entre $\theta_0$ et $d$ [math] :
$$ d(x_F) = d_{ref} - D_{sc-oe}\tan\theta_0 $$
à une constante prés $d_{ref}$ prise pour référence exemple le réglage à 5m.
Or la relation trigonométrique suivante :
$$ \sin 2 x = \frac{2 \tan x}{1+\tan^2 x} $$
permet de transformer Eq.1 en une équation sur $\tan\theta_0 = t_0$ à savoir :
$$ \frac{x_F}{2 x_F^{max}} t_0^2 - t_0 + \frac{x_F}{2 x_F^{max}} + \frac{h}{x_F} = 0 $$
La résolution est à la portée d’un élève de 3eme. Il y a en principe 2 solutions mathématiques
$$ t_0^{\pm} = \frac{x_F^{max}}{x_F} (1 \pm \sqrt{\Delta}) $$
avec
$$ \Delta = 1 - 2\frac{h}{x_F^{max}} - \left(\frac{x_F}{x_F^{max}}\right)^2 $$
Dans les cas pratiques $\Delta$ a peu de chance d’être négatif car $ x_F^{max}\gg x_F, h$ donc point de solutions « complexes » (Ouf !). Ceci dit on aurait 2 solutions réelles… C’est là où on se rappelle du cas limite à très grande vitesse. Dans ce cas $x_F^{max}$ tend aussi vers de très grande valeur. Alors, on s’aperçoit dans ce cas que
$$ t_0^{\pm} \approx \frac{ x_F^{max} }{x_F}\left( 1 \pm (1- h/x_F^{max})\right) $$
La seule solution possible c’est celle avec le signe $-$ car elle donne :
$$ t_0 = \tan\theta_0= t_0^{-} \approx h/x_F = \tan\theta_F $$
Donc finalement, on peut écrire l’expression (compacte) donnant le réglage du viseur :
$$ \boxed{ d(x_F) = d_{ref}- D_{sc-oe} \times \frac{x_F^{max}}{x_F} \left( 1 - \sqrt{1- 2(h/x_F^{max}) - (x_F/x_F^{max})^2} \right) } \quad(2) $$
Un exemple
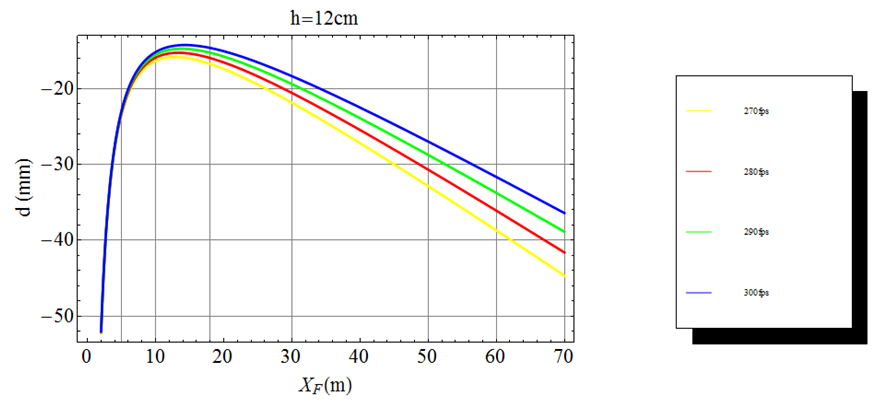
Sur la série de photos suivantes, on s’aperçoit que la hauteur $h$ peut être de l’ordre de la distance entre le bas du menton est la ligne des yeux soit environ 12cm.

Dans ces conditions la formule Eq.2 donne le graphe suivant dont chaque courbe représente le cas d’une vitesse initiale de la flèche de 270 (jaune), 280 (rouge), 290 (vert) et 300fps (bleu).
On constate que les réglages à « petites » distances (<10m) sont identiques à ceux des « grandes » distances (>20m). Le réglage à 5m quasi-indépendant de la vitesse de sortie de flèche se retrouve entre 25 et 35m selon que l’on a 270 ou 300fps.
Et cela n’affecte pas uniquement les armes avec viseur comme on peut le constater sur les deux figures ci-dessous.
Dans ce cas on note néanmoins que la distance $h$ est plus petite, de l’ordre de la hauteur de quelque doigts, soit environ 6cm. Dans ces conditions, on obtiendrait le schéma suivant (en gardant les vitesses d’éjection identiques) :
La transition "petites/grandes" distances se fait plutôt que précédemment, plus prés de 10m dans le cas considéré ici.
Conclusion
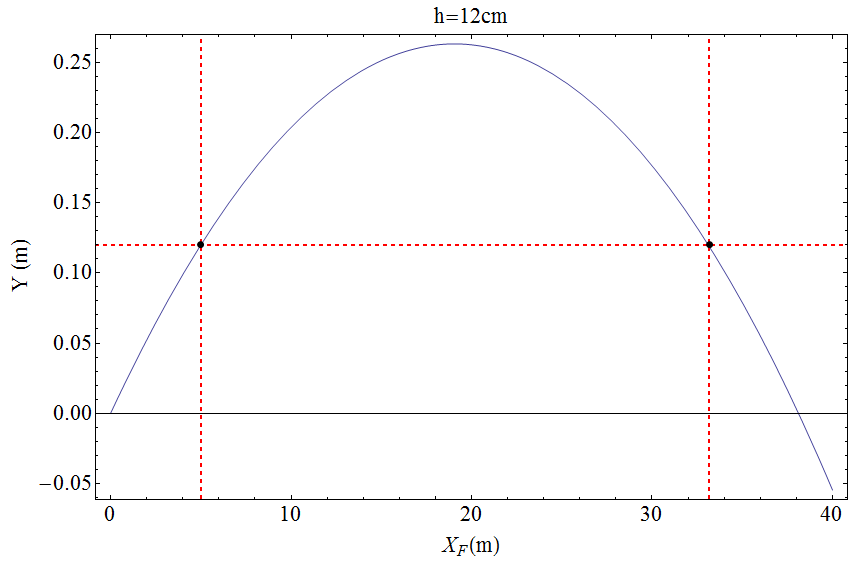
Bien entendu toutes les valeurs numériques ne sont données qu’à titre indicatif qui plus est la résistance de l’air n’a pas été prise en compte. Par contre, l’effet constaté par bon nombre d’archers de parcours de la redondance de leur réglage entre petites et grandes distances, s’explique par le simple décalage de la flèche par rapport à la ligne de visée.. Donc une histoire de balistique ! Pour les cibles proches la flèche atteint la cible sans passer par son point culminant, d’où la quasi-indépendance du réglage à 5m vis-à-vis de la vitesse d’éjection ; pour les longues distances la flèche atteint la cible dans sa phase de descente. Ceci peut se schématiser simplement
où la même parabole coupe la ligne de visée en 2 positions, une à courte distance et l’autre à longue distance (ici $v_0= 270$fps).
Je pense que cela dissipera bon nombre de malentendus. Enfin, merci à quelques collègues de l’ACA pour les photos.
Epilogue
Refaisant des réglages en salle, j’en ai profité pour faire mon abaque entre 5m et 22m. Je peux me servir même de ces mesures pour ajuster les paramètres Distance oeil-scope,
Distance oeil-encoche et vitesse de sortie.
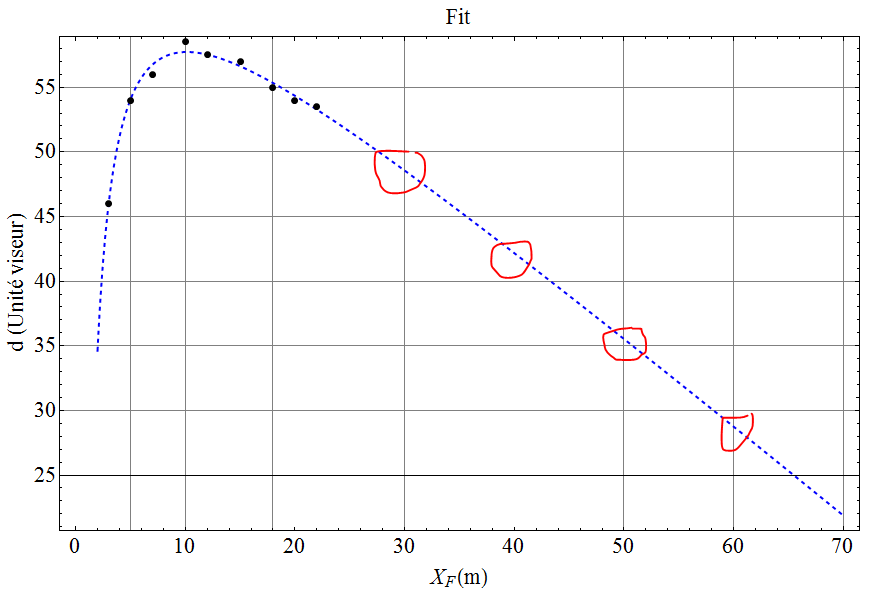
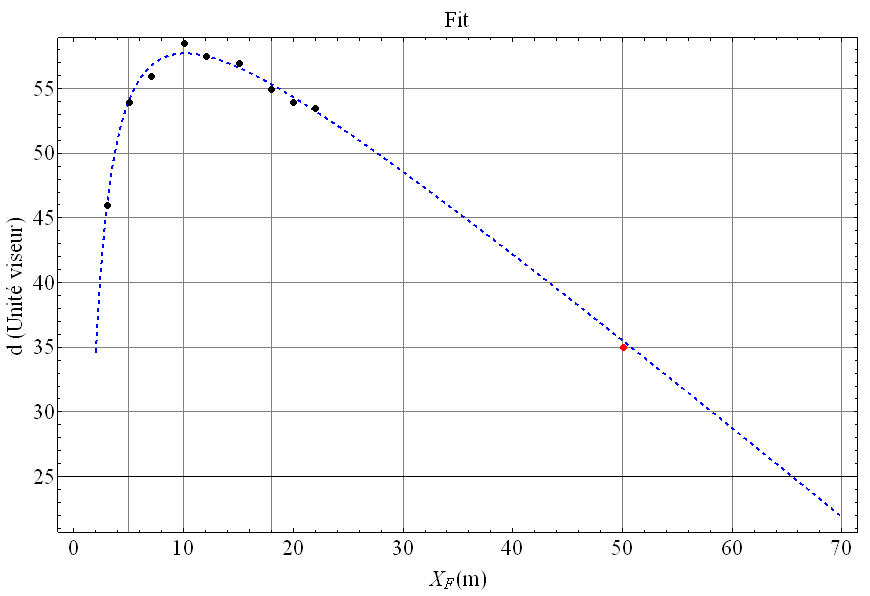
Voici le résultat (sans trucage !) :
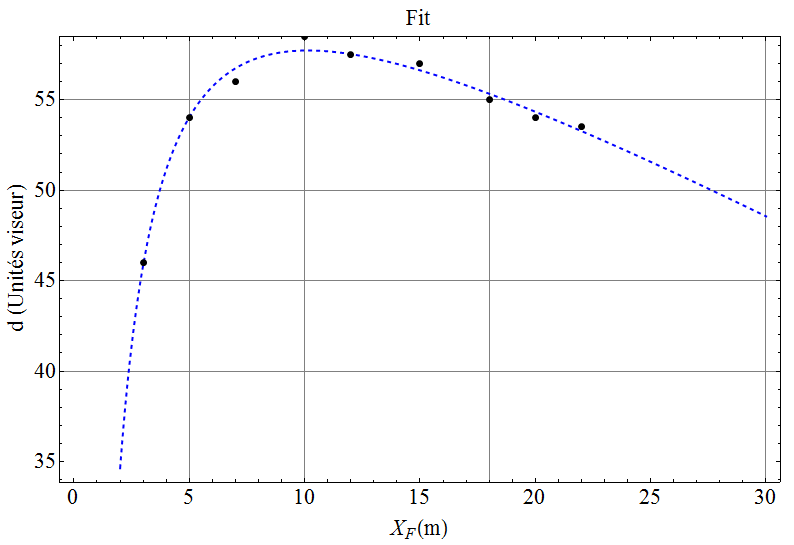
Les paramètres ajustés sont tout à fait plausibles (attention aux minima locaux et à faire la traduction des mesures de l’index du viseur en mm et vice-versa) :
- Distance oeil-scope = 78.2cm
- Distance oeil-encoche = 9.7cm
- vitesse de sortie = 237fps (oui mon arc est mou lent à 40lbs)
Ma tendre et chère épouse qui n’y connait rien en TAA a mesuré les deux premiers paramètres sans que je ne lui dise rien du pourquoi de la chose (pour pas l’influencer) :
- Distance oeil-scope = 79cm (mesure difficile selon elle car j’ai des lunettes...)
- Distance oeil-encoche = 9.5cm (elle a faillit me mettre le régler dans l’oeil :) !
Puis j’ai utilisé mon Chrony (chronographe pour petits projectiles) pour mesurer la vitesse de sortie de flèche : - entre 71.75 et 71.34 m/s soit entre 234 et 235fps.
Je trouve que l’accords mesure - fit est excellent !
Donc, en salle on peut se préparer son abaque et voir sur le terrain ce que ça donne aux plus grandes distances
Le 23/03/13 j’ai pu faire des tirs a 50m et je n’avais pas mon abaque ! 1 ACE de flinguée... bon me souvenant de tête le plot ci-dessus j’ai pu corriger et in fine voici en rouge le point de mesure. Ca colle parfaitement...