#*Introduction

Dans l’article Image de la cible (scope, point de visée, rétine...), j’ai montré comment obtenir relativement simplement l’image de la cible à travers le scope et une version simplifiée de l’oeil.

En principe l’image de la cible est "toujours" floue si l’oeil voit bien le point de visée collé/fixé sur la lentille du scope. En effet, l’oeil ne peut accommoder le cristallin à la fois pour rendre nette l’image de la cible et celle du scope lui-même.

Tirer avec une image floue de la cible mais un point de visée net est tout à fait acceptable et présente des avantages mais certaines personnes ne sont pas à l’aise. Le flou est particulièrement handicapent surtout quand on veut utiliser de forte puissance de scope.

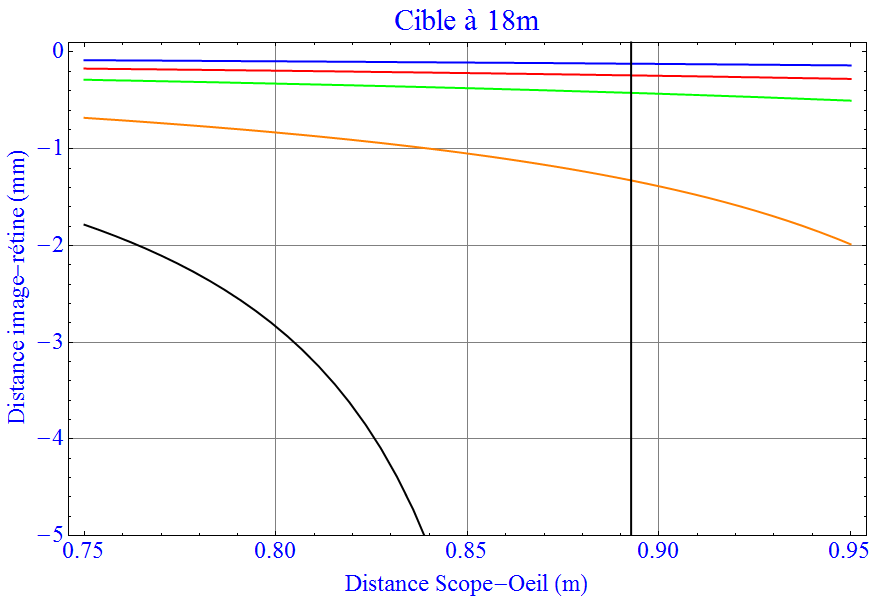
Pour rappel, sur le graphique suivant (tiré de l’article cité plus haut) est montré le résultat sur la distance entre la rétine et l’image à travers le système "scope+oeil" en fonction de la distance entre le scope et l’oeil (en abscisse) et différente valeur de dioptrie de la lentille du scope : 0.6 (bleu), 0.7 (rouge), 0.8 (vert), 1.0 (orange) et 1.2 (noir). La singularité du grossissement (tendant vers l’infini) est visible sur la courbe noir.

Visette correctrice

Avant d’envisager ce que fait la visette correctrice usuelle en association avec les lentilles de scope, il y a 2 points à connaître :

• il y a des visettes sans correction, c’est-à-dire que ce ne sont que des simples trous (diaphragmes), ce sont celles que j’utilise. Plus le trou est petit :
  • plus la quantité de lumière diminue (par le carré du diamètre du trou étant donné que c’est un effet de surface),
  • et plus il sélectionne des rayons lumineux proches de l’axe optique. On s’affranchit d’autant mieux des défauts de la définition de l’image d’un point : chromaticité ou dépendance de la convergence en fonction de la longueur d’onde ou de la couleur, aberration géométrique... L’image est donc d’autant plus nette. Corollaire il faut utiliser des lentilles de scope d’excellente qualité.
• il existe des visettes correctrices qui ne s’associent pas avec un scope car précisément se sont de petits scopes. Elles sont essentiellement utilisées pour la chasse (voir tir 3D, y-at’il des lecteurs utilisant ces visettes ?) car ainsi les personnes tirent sans lunette ou lentilles correctrices. Le scope en lui-même est donc dépourvu de lentille mais porte uniquement des points de visée. En anglais on les appelle les "verifiers".

Revenons donc aux visettes classiquement associées aux scopes ("clarifier" en anglais). La figure suivante fixe les notations des distances entre la cible, le scope, la visette, l’oeil et la l’image finale. La dioptrie du scope sera notée $\delta_{sco}>0$, celle de la visette (lentille divergeante) $-\delta_v <0 $ et celle de l’oeil $\delta_{oe}$.

L’usage du formalisme matriciel permet d’introduire simplement la visette

$$ \begin{align*} \begin{pmatrix} y_2 \\ \theta_2 \end{pmatrix} &= \begin{pmatrix}1 & d_2 \\ 0 & 1 \end{pmatrix} \begin{pmatrix}1 & 0 \\ -\delta_{oe} & 1 \end{pmatrix} \begin{pmatrix}1 & d_{soe}-d_{v} \\ 0 & 1 \end{pmatrix} \\ &\times \begin{pmatrix}1 & 0 \\ \delta_{v} & 1 \end{pmatrix} \begin{pmatrix}1 & d_v \\ 0 & 1 \end{pmatrix} \begin{pmatrix}1 & 0 \\ -\delta_{sco} & 1 \end{pmatrix} \begin{pmatrix}1 & d_1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} y_1 \\ \theta_1 \end{pmatrix} \end{align*} $$

$$ d_2^{D\rightarrow\infty} = \frac{-1+d_{soe}\delta_{sco}+(d_{soe}-d_{sv})(-1+d_{sv}\delta_{sco})\delta_v}{-\delta_{oe}-\delta_{sco}+d_{soe}\delta_{oe}\delta_{sco}+(-1+(d_{soe}-d_{sv})\delta_{oe})(-1+d_{sv}\delta_{sco})\delta_v} $$

En pratique la société Arc Système [1] fournit des visettes correctrices non seulement de tailles de trou différentes mas aussi déclinées en trois valeurs de dioptrie : -1, -2 et -3.

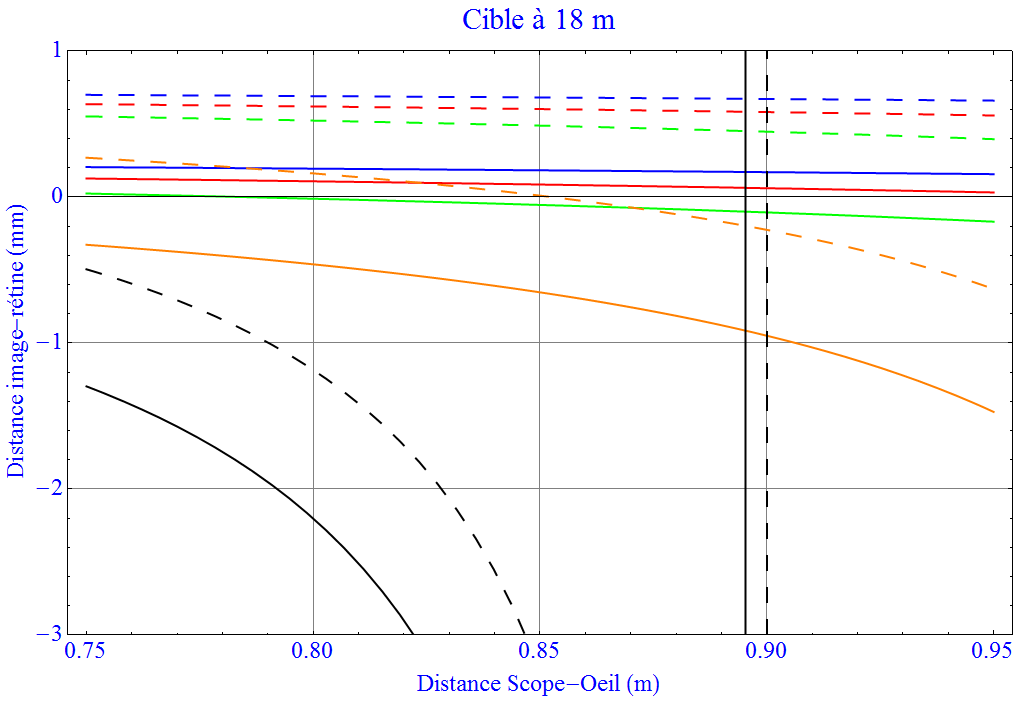
Sur le graphique ci-dessous je montre le même type de courbes que précédemment mais cette fois avec une visette correctrice située à une distance de l’oeil fixe de 7cm de mon oeil. Les courbes en trait plein (trait tiré) sont effectuées avec une visette de dioptrie -1 (-3). L’oel est toujours dans sa position de repos avec une dioptrie de 60.

On constate :

• plus la correction de la visette est forte plus l’image est en avant de la rétine
• à une distance de 85cm (mon cas nominal) la correction -3 rend parfaitement nette une cible vue par une lentille de 1.0 dioptrie (courbes orange).
• aucune correction ne peut rendre nette l’image vue par une lentille de 1.2 dioptrie (courbes noires).

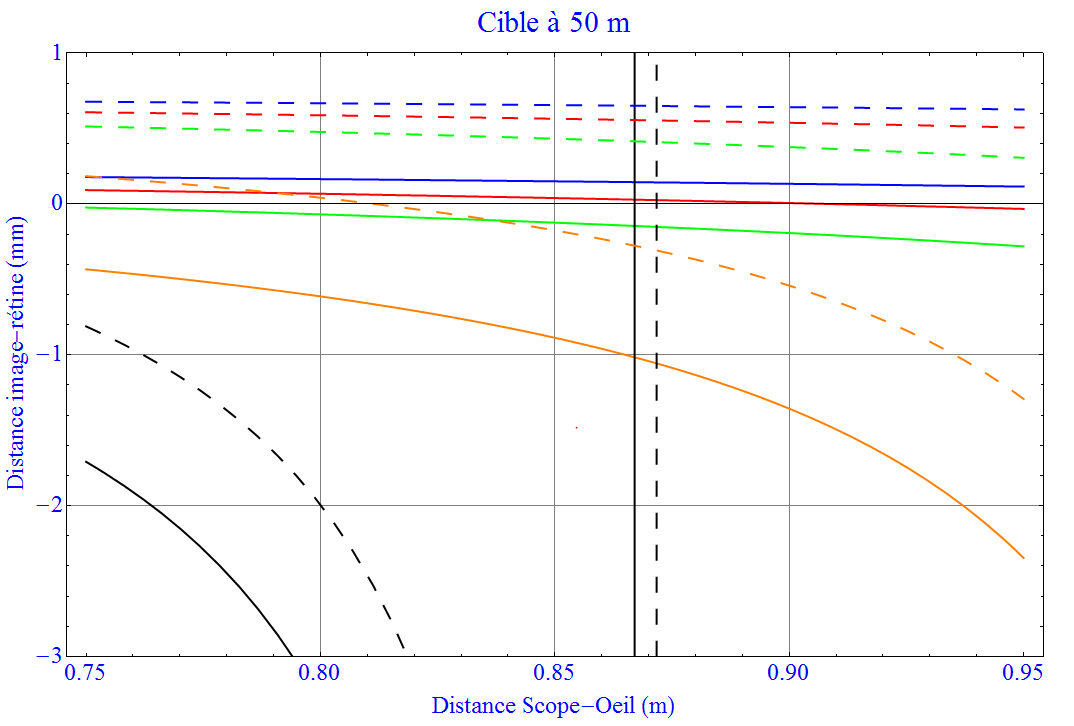
Pour une cible à 50m il faudra raccourcir de 5cm ( 2in) la distance du scope à l’oeil pour pouvoir rendre nette la cible vue par un scope de 1.0 dioptrie.

Résumé

Cet article complète l’étude de l’image de la cible vue par l’oeil à travers le système optique constitué du scope et d’une éventuelle visette. Même si je n’utilsie pas de visette correctrice car :

• la lumière devant traverser une lentille supplémentaire cela réduit d’autant la luminosité
• en plein air, elle devienne inutilisable dès lors que de la buée ou une goutte d’eau se loge dans le trou
• l’image floue associée à un point de visée net est une alternative qui fonctionne et j’ai montré dans l’article Image de la cible (scope, point de visée, rétine...) comment choisir la puissance de sa lentille et la dimension de son point de visée.

Mais j’espère que les aficionado des visettes correctrices auront du grain à moudre.