Introduction
Dans l’article Image de la cible (visette) j’avais donné des indications sur la modification de l’image de visée par l’usage de visettes correctrices ayant une lentille (divergente) d’un diamètre de l’ordre du millimètre (voir Visette Arc System (code couleur) pour les visettes Arc Système). Mais en fait, beaucoup d’archers se passent de cette lentille correctrice en s’accommodant d’une image plus ou moins floue de la cible. Il y a des avantages mais je n’y reviens pas. En fait, beaucoup on constatait devoir ajuster le diamètre du trou au grès de différentes conditions de luminosité, extérieur/intérieur, de leur humeur peut-être... Le constat est souvent un agacement plus ou moins marqué ou un certain fatalisme. J’aimerai apporter quelques explications et donner raison aux derniers.
Que fait le trou ?
L’effet d’interposer un trou de rayon $r$ entre une image est un plan à distance $d$ du trou est un phénomène bien connu des photographes : le sténopé.

Mais si les premières descriptions en Chine et en Occident datent d’environ 400 av. J.C, des mesures fiables sont relativement récentes (1989) et permettent d’avoir une description cohérente du phénomène faisant le lien entre l’Optique Géométrique et l’Optique en champ lointain (diffraction de Fraunhofer).
Matt Young en analysant des photos de feuilles sur lesquelles étaient dessinées des rectangles noirs plus ou moins larges et plus ou moins espacés, il a pu mesurer le pouvoir de séparation entre 2 points sur le plan focal en fonction d’une variable sans dimension qui n’est autre que la distance $d$ exprimée en unité de $\lambda/r^2$, avec $\lambda$ la longueur d’onde de la lumière éclairant les feuilles. Le résultat est donné sur la figure ci-dessous.
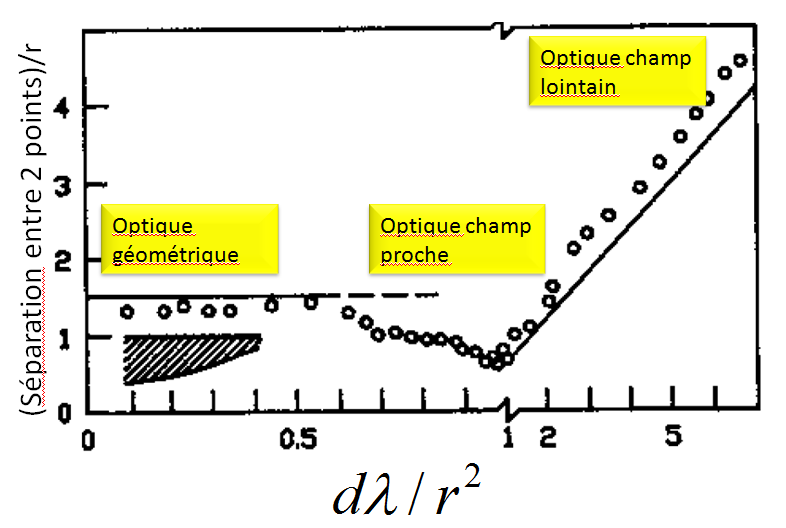
Les deux lignes noires qui montrent l’évolution des cercles (données expérimentales) peuvent se comprendre car correspondent à deux cas limites. Par exemple examinons l’effet de changer le rayon $r$ de 2 trous et voyons comment l’on peut distinguer l’image produite par ces 2 trous sur le plan focal distant de $d$ :
- à grandes valeurs de $r$, 2 trous occultent une région bien précisent et donc 2 points seront confondus sur le plan focal s’ils sont à une distance inférieure à environ $\Delta \approx 1,5 r$. C’est de l’optique géométrique où les rayons lumineux issus de la feuille et traversant le trou ne sont pas déviés avant d’arriver sur le plan de la photo. Ainsi $\Delta/r$ est une constante.
- à petites valeurs de $r$, chaque trou devient un obstacle majeur et le phénomène de diffraction prend place modifiant la direction de propagation des rayons lumineux au passage du trou. L’angle de déflexion est de $\theta\approx 0.61 \lambda/r$ (rad). Un peu de géométrie donne la séparation minimale $\Delta$ que doivent les 2 trous pour ne pas mélanger les 2 images :
$$ \Delta \approx 2 d \theta \Rightarrow \frac{\Delta}{r} \approx 1.22 \frac{d\lambda}{r^2} $$
Donc $\Delta/r$ est une fonction linéaire de $d\lambda/r^2$.
On remarque que les 2 courbes se coupent environ pour $d\lambda/r^2 \approx 1$.
Le passage de la lumière à travers un trou est donc rendu compte par le schéma suivant montrant les différentes zones où s’applique des "optiques" différentes.

Aux environs zone intermédiaire, dite de "champ proche" l’optique n’est pas prédictible par des arguments simples. Il y a des phénomènes d’interférences avec des alternances de zones plus ou moins sombres.
On peut néanmoins définir une focale équivalente du trou (ou dioptrie, inverse de la focale) :
$$ \delta_{trou} = 1/f = \lambda/r^2 = 4 \lambda/ D^2 $$
La figure ci-dessous donne les valeurs de $\delta_{trou}$ pour la plage de diamètre $D$ utile en pratique et pour 3 longueurs d’onde de la lumière visible (bleu : 436nm, vert : 546nm et rouge : 700nm).

Comme la dioptrie varie en fonction du diamètre, on comprend également pourquoi l’on peut plus ou moins rendre l’image flou/nette en changeant de diamètre.
On voit également l’extrême sensibilité de la dioptrie en fonction de la longueur d’onde pour un diamètre donné. Or cela a une conséquence immédiate, selon le type d’éclairage la pondérations en RGB (Red/Green/Blue) est différente, donc la dioptrie moyenne va changer !!! D’où le constat que notre perception de netteté varie quand on passe de l’extérieur à l’intérieur, et selon le type d’éclairage artificiels dans les gymnases plus ou moins "froid" (c-à-d plus ou moins tirant sur le bleu ou le jaune). Pour mémoire l’oeil humain a une maximum de sensibilité dans le jaune-vert.
Conclusion
Le phénomène de sténopé permet de rendre compte de la variation de la dioptrie équivalente qui dépend du diamètre du trou ET du spectre de l’éclairage. Notre perception de l’image de la cible à travers ce simple trou de visette est donc bien un phénomène dépendant de la vision de l’archer mais aussi des conditions d’éclairages. Il faut donc se résigner à changer de diamètre de trou pour s’adapter aux conditions que l’on ne maîtrise pas... Cela fait le bonheur des vendeurs de visette.