Introduction
Dans les articles consacrés à l’étude de la trajectoire d’une flèche (voir la liste dans A l’attention des TPE, TIPE et autres étudiants) j’ai toujours considéré que la gravité locale correspond à la verticale du lieu et que durant le temps de vol la Terre reste un référentiel galiléen ou inertiel. Mais on sait bien que la Terre tourne et quelle n’est pas ronde ! Alors faut-il revoir sa copie ?
Nous allons d’abord aborder le problème de changement de repère d’une manière générale, puis dans le cas terrestre. Dans ce cas la Terre est considérée comme mue par un mouvement de rotation constant sur elle-même à savoir une révolution en 24h autour d’un axe de direction fixe par rapport à un référentiel héliocentrique [1].
Changement de repère d’un vecteur dépendant du temps
Dans la figure 1 j’ai représenté 2 repères R et R’, le premier est fixe (ou inertiel) et le second est en mouvement par rapport au premier. On note $\vec{V}(R{’}/R)$ et $\vec{\Omega}(R^{’}/R)$ respectivement la vitesse et la rotation instantanées de R’ par rapport à R (cf. ces deux vecteurs dépendent du temps) [2].

Prenons une fonction vectorielle quelle conque $\vec{K}_{R{’}}(t) $ dépendante du temps et exprimée dans le repère R’ selon
$$ \vec{K}_{R^{’}}(t) = \alpha^{’}(t) \vec{i^{’}} + \beta^{’}(t) \vec{j^{’}} + \gamma^{’}(t) \vec{k^{’}} $$
Notez bien que dans le repère R’ seules dépendent du temps les coordonnées $( \alpha^{’}(t), \beta^{’}(t), \gamma^{’}(t))$. Par contre, quand on s’intéresse à l’évolution de ce vecteur dans le repère R alors non seulement les coordonnées dépendent du temps mais aussi l’orientation des 3 axes $(\vec{i^{’}},\vec{j^{’}},\vec{k^{’}})$. Donc quand on veut calculer la dérivée par rapport au temps dans le repère R il vient :
$$ \left(\frac{d\vec{K}}{dt}\right)_{R} = \frac{\alpha^{’}}{dt}\vec{i^{’}} +\alpha^{’} \frac{d\vec{i^{’}} }{dt} + \dots $$
où je n’ai fait figurer que les conséquences pour la première coordonnée puisque pour les autres la procédure est identique. Or le trièdre $(\vec{i^{’}},\vec{j^{’}},\vec{k^{’}})$ peut être considéré comme un « solide » et on utilise un résultat sur les torseurs qui dit qu’il existe à tout moment un vecteur instantané qu’on note $\vec{\Omega}_{R^{’}/R}(t)$ tel que :
$$ \frac{d\vec{i^{’}}}{dt} = \vec{\Omega}_{R^{’}/R}(t) \wedge \vec{i^{’}} $$
Le $\wedge$ est l’opérateur de produit vectoriel entre 2 vecteurs. Donc, on peut noter finalement que les dérivées de $\vec{K }$ d’un repère à l’autre sont liées par :
$$ \left(\frac{d\vec{K}}{dt}\right)_{R} = \left(\frac{d\vec{K}}{dt}\right)_{R^{’}} + \vec{\Omega}_{R^{’}/R}(t) \wedge \vec{K} $$
Ou bien
$$ \left(\frac{d\vec{K}}{dt}\right)_{R{’}} = \left(\frac{d\vec{K}}{dt}\right)_{R} - \vec{\Omega}_{R^{’}/R}(t) \wedge \vec{K} $$
Le premier membre de l’égalité est exprimé dans le repère R’ tandis que le second l’est dans le repère R.
Application à la vitesse
Maintenant appliquons ce que nous venons de démontrer au cas de la vitesse d’un point mobile M. On sait que l’addition vectorielle fournit la relation $\vec{SM} = \vec{SO}+\vec{OM}$. Si l’on dérive cette relation dans le repère R, le mouvement du point O doit être pris en compte, il vient :
$$ \vec{V}_R(M) = \vec{V}_R(O) + \left(\frac{d\vec{OM}}{dt}\right)_R $$
Le dernier terme du membre de droite est remplacé par application du résultat de la section précédente,
$$ \vec{V}_R(M) = \vec{V}_{R{’}}(M) + \vec{V}_R(O) + \vec{\Omega}_{R^{’}/R}\wedge \vec{OM} $$
Si on regroupe les termes calculés dans les deux repères, il vient alors
$$ \vec{V}_{R{’}}(M) = \vec{V}_R(M) - \vec{V}_R(O) - \vec{\Omega}_{R^{’}/R}\wedge \vec{OM} $$
En quelques sortent pour le point M il existerait une vitesse d’entrainement dont l’origine est purement liée au mouvement du repère R’
Application à l’accélération
Poursuivons en dérivant une nouvelle fois par rapport au temps pour obtenir la relation qui lie les accélérations du point M calculées dans les deux repères.
$$ \begin{align*} \left(\frac{d\vec{V}_R(M)}{dt}\right)_R &= \left(\frac{d\vec{V}_R(O)}{dt}\right)_R + \left(\frac{d\vec{V}_{R^{’}}(M)}{dt}\right)_R \\ &+ \left(\frac{d \vec{\Omega}_{R^{’}/R}}{dt}\right)_R \wedge \vec{OM} + \vec{\Omega}_{R^{’}/R}\wedge \left(\frac{d\vec{OM}}{dt}\right)_R \end{align*} $$
Notons tout d’abord une identité si on prend $\vec{K}=\vec{\Omega}_{R^{’}/R}$ alors
$$ \left(\frac{d \vec{\Omega}_{R^{’}/R}}{dt}\right)_R = \left(\frac{d \vec{\Omega}_{R^{’}/R}}{dt}\right)_{R^{’}} + \vec{\Omega}_{R^{’}/R} \wedge \vec{\Omega}_{R^{’}/R} $$
Or le second terme du membre de droite est strictement nul par définition de l’opérateur $\wedge$ donc nous noterons
$$ \left(\frac{d \vec{\Omega}_{R^{’}/R}}{dt}\right)_R = \left(\frac{d \vec{\Omega}_{R^{’}/R}}{dt}\right)_{R^{’}} $$
indépendamment du repère R ou R’.
Ensuite il est maintenant aisé de dériver que
$$ \left(\frac{d \vec{V}_{R^{’}}(M)}{dt}\right)_R = \left(\frac{\vec{V}_{R^{’}}(M)}{dt}\right)_{R^{’}} +\vec{\Omega}_{R^{’}/R} \wedge \vec{V}_{R^{’}}(M) $$
et en utilisant la loi sur les vitesses, il vient finalement :
$$ \begin{align*} \left(\frac{d\vec{V}_R(M)}{dt}\right)_R &= \left(\frac{d\vec{V}_R(O)}{dt}\right)_R + \left(\frac{d\vec{V}_{R^{’}}(M)}{dt}\right)_{R^{’}} \\ & + \dot{\vec{\Omega}}_{R^{’}/R}\wedge \vec{OM} + \vec{\Omega}_{R^{’}/R} \wedge \left(\vec{\Omega}_{R^{’}/R}\wedge \vec{OM} \right) \\ & + 2 \vec{\Omega}_{R^{’}/R} \wedge \vec{V}_{R^{’}}(M) \end{align*} $$
On peut simplifier cette expression en primo notant $\vec{\Omega} = \vec{\Omega}_{R^{’}/R}$ et secundo en reconnaissant que la dérivée calculée dans un repère de la vitesse calculée dans ce même repère n’est autre que l’accélération du point dans ce même repère, qu’on note finalement $\vec{\gamma}(M)$. Donc,
$$ \begin{align*} \vec{\gamma}_R(M) &= \vec{\gamma}_{R^{’}}(M) + \vec{\gamma}_R(O) + \dot{\vec{\Omega}}\wedge \vec{OM} + \vec{\Omega} \wedge \left(\vec{\Omega}\wedge \vec{OM} \right) \\ &+ 2 \vec{\Omega} \wedge \vec{V}_{R^{’}}(M) \end{align*} $$
ou d’une façon similaire en regroupant quelques termes :
$$ \begin{align*} \vec{\gamma}_{R^{’}}(M) &= \vec{\gamma}_R(M) - \vec{\gamma}_R(O) \\ & - \dot{\vec{\Omega}}\wedge \vec{OM} - \vec{\Omega} \wedge \left(\vec{\Omega}\wedge \vec{OM} \right) - 2 \vec{\Omega}\wedge \vec{V}_{R^{’}}(M) \end{align*} $$
C’est cette expression qui va donner lieu à matière à discuter de la validité des approximations faites dans les articles consacrés au vol de flèche.
Application au cas de la Terre
Dans l’expression précédente si on place le repère R au centre du Soleil et R’ au centre de la Terre avec $\vec{\Omega} = \Omega \vec{k}_0$ constant, alors
$$ \begin{align*} \vec{\gamma}_{R_{T}}(M) &= \vec{\gamma}_S(M) - \vec{\gamma}_S(O) \\ & - \Omega^2 \vec{k}_0 \wedge (\vec{k}_0 \wedge \vec{OM})- 2 \Omega \vec{k}_0 \wedge \vec{V}_{R_T}(M) \end{align*} $$
Nous allons voir quelles sont les implications des 3 termes signés “-“ du membre de droite.
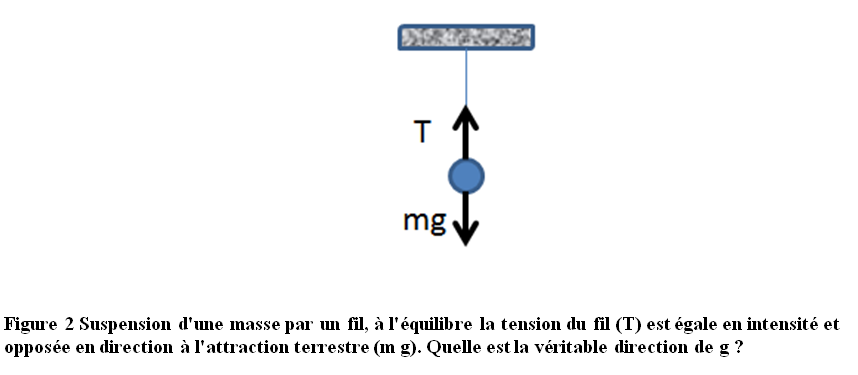
Expérience statique du fil à plomb : gravité locale
L’usage de suspension d’une masse au bout d’un fil est très courante pour déterminer la verticale du lieu par les maçons, mais est-ce bien la verticale au sens stricte même dans le cas d’une Terre parfaitement ronde en rotation ???
Si la masse est au repos alors $\vec{V}_{R_T}(M) = \vec{\gamma}_{R_{T}}(M) = \vec{0}$. Donc
$$ \begin{align*} \vec{T} &= m \left( \left[\vec{G}_T(M) - \Omega^2 \vec{k}_0 \wedge (\vec{k}_0 \wedge \vec{OM}) \right] + \left[\vec{G}_{As}(M) - \vec{\gamma}_S(O) \right] \right)\\ &= m \left[\vec{g}_0(M) + \delta\vec{g}(M,As)\right] \end{align*} $$
Avec $\vec{G}_T$ et $\vec{G}_{As}$ les attractions gravitationnelles dues à la Terre et les autres astres (cf. Lune, Soleil…). La dernière égalité indique une sorte de hiérarchie numérique, en effet il se trouve qu’un calcul d’ordre de grandeur fourni la relation suivante si l’on considère un seul astre perturbateur :
$$ \frac{\delta g}{g_0} \approx \frac{M_{As}}{M_T}\left( \frac{R_T}{d_{T-As}} \right)^3 $$
faisant intervenir le rapport de la masse de l’astre à celle de la Terre ainsi que le rapport du rayon de la Terre à la distance Terre-Astre. Pour les cas de la Lune et du Soleil par exemple, on trouve que ce rapport est de l’ordre de $10^{-7}$ et $0.510^{-7}$ ce qui montre 1) que ce rapport est très faible et justifie la hiérarchie annoncée, et 2) que Lune et Soleil doivent être pris sur un même pied d’égalité si on veut inclure ces termes sous-dominants. En fait ce terme « petit » $\delta g$ pour des applications de la vie courante est néanmoins responsable des marées ! et dans ce cas on sait bien que Lune ET Soleil sont à prendre en compte pour expliquer (avec les particularités locales) ce phénomène côtier.
Bon, négligeons pour la suite $\delta g$ et concentrons nous sur le terme dominant
$$ \vec{g}_0(M) = \vec{G}_T(M) - \Omega^2 \vec{k}_0 \wedge (\vec{k}_0 \wedge \vec{OM}) $$
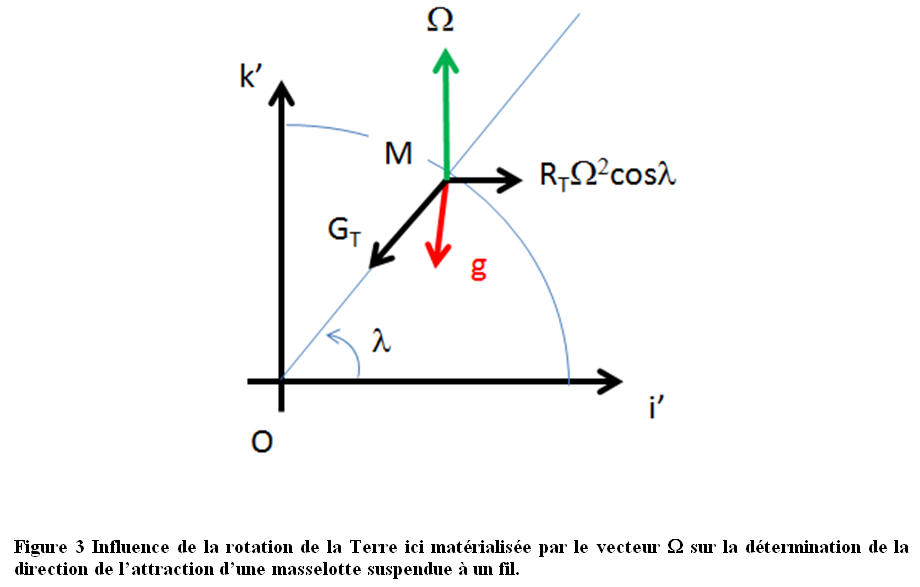
Sur la figure 3, j’ai représenté les différents termes rentrant dans le calcul de $\vec{g}_0(M) $. Tout d’abord si la Terre est ronde et homogène, la direction de $\vec{G}_T(M)$ pointe vers son centre O réelle verticale locale. Ensuite, on fixe l’orientation du repère pour que l’axe $\vec{k^{’}}=\vec{k}_0 $ alors le calcul du second terme est aisé si l’on introduit $\lambda$ la latitude du lieu, il vient
$$ \Omega^2 \vec{k}_0 \wedge (\vec{k}_0 \wedge \vec{OM}) = - \Omega^2 R_T \cos\lambda \vec{i^{’}} $$
La rotation de la Terre est donc une action centrifuge qui fait dévier la direction de $\vec{g}_0(M)$ de la verticale :
$$ \vec{g}_0(M) = - G_T \cos\lambda \left( 1 - \frac{R_T \Omega^2}{G_T} \right) \vec{i^{’}} - G_T\sin\lambda \vec{k^{’}} $$
On voit que la déviation centrifuge est gouvernée par un paramètre sans dimension
$$ \epsilon = \frac{R_T \Omega^2}{G_T} \approx 3.5\ 10^{-3} $$
Donc la correction en intensité par rapport à la valeur de $G_T$ est très faible, et concernant la déviation à la verticale locale on peut montrer quelle est de l’ordre de
$$ \alpha \approx \frac{1}{2}\epsilon \sin 2\lambda \approx 1.7\ 10^{-3}\ rad \approx 6’ \quad (\mathrm{minutes\ d’arc}) $$
donc là aussi pour les applications courantes elle est négligeable.
Si on se mettait à prendre en compte cette déviation centrifuge, il faudrait d’abord se poser la question de la valeur et direction de $\vec{G}_T(M)$ car non seulement la Terre n’est pas homogène mais n’a rien d’une sphère idéale (voir les articles liés à celui concernant le géoïde).
Dans la suite nous supposerons que la verticale du lieu est donnée par la direction de $\vec{g}$ dont l’intensité est prise constante et j’enlève l’indice "0" et la mention du point M pour alléger la notation.
Projectile en mouvement
Pour arriver à ce point nous avons déjà parcouru un long chemin, il nous faut à présent découvrir l’effet de la rotation de la Terre sur un objet en mouvement et soumis à l’attraction terrestre (voir approximation de la section précédente). On va se rapprocher de cas étudiés dans la série d’articles liés au vol d’une flèche (enfin !).
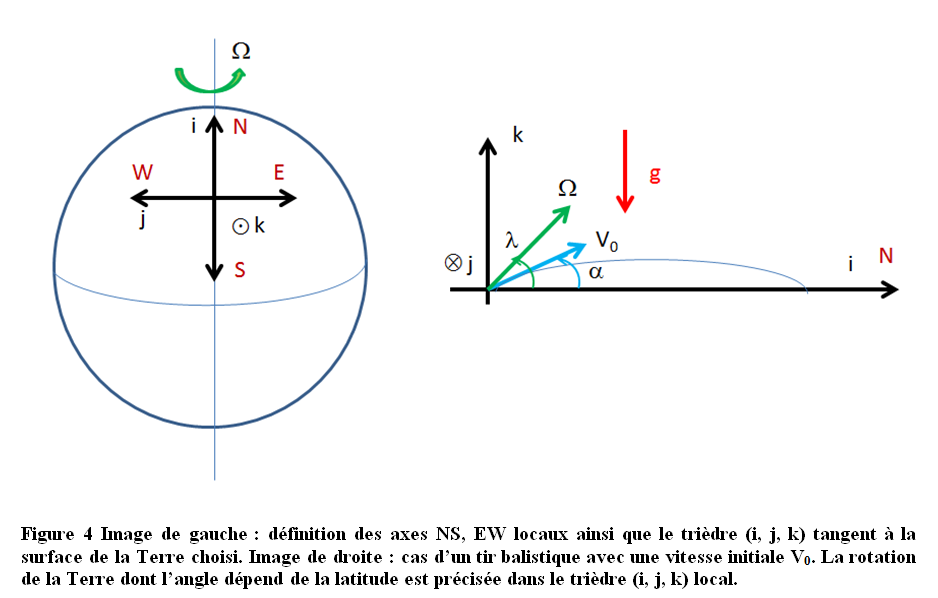
Dans un premier temps faisons abstraction de la rotation de la Terre. Si on tire selon un axe Nord-Sud (voir Figure 4), on sait qu’en fonction du temps les coordonnées du vecteur vitesse et de la position du point M s’expriment selon
$$ \begin{array}{rcl} \dot{x}(t) &=& V_0 \cos\alpha \\ \dot{y}(t) &=& -g t + V_0 \sin\alpha \end{array} $$
et
$$ \begin{array}{rcl} x(t) &=& V_0 \cos\alpha\ t \\ y(t) &=& -\frac{1}{2}g t^2 + V_0 \sin\alpha\ t \end{array} $$
Le temps de vol au bout duquel le projectile retombe à terre est égal à
$$ t_{vol} = \frac{V_0\sin\alpha}{g} $$
et la distance parcourue est quant à elle donnée par l’expression
$$ x_{vol} = \frac{ V_0^2\sin\alpha \cos\alpha}{g} $$
Maintenant si nous prenons en compte la rotation terrestre journalière, les forces exercées sur le projectile sont non seulement la pesanteur mais aussi la fameuse force de Coriolis :
$$ \vec{F} = m\vec{\gamma}(M) = m\vec{g} -2 m \vec{\Omega}\wedge\vec{V}_{R_T}(M) $$
Primo, on va traiter la force de Coriolis comme une perturbation par rapport à l’effet de la pesanteur donc la vitesse qui apparait dans sa définition peut être pris comme celle déduite du calcul où seule la pesanteur joue. Il vient donc
$$ \vec{F}_c = -2 m \vec{\Omega}\wedge\vec{V}_{R_T}(M) = -2 m \vec{\Omega}\wedge \left(\vec{V}^{g}_{R_L}(M) +\dots\right) $$
En exprimant les vecteurs dans le repère local R_L :
$$ \vec{\Omega} = \left( \begin{array}{c} \Omega \cos\lambda\\ 0\\ \Omega \sin\lambda\\ \end{array} \right) $$
et
$$ \vec{V}^{g}_{R_L}(M) = \left( \begin{array}{c} V_0\cos\alpha\\ 0\\ -* gt+V_0 \sin\alpha\\ \end{array} \right) $$
D’où l’expression de la force de Coriolis dans ce repère local
$$ \vec{F}_c = -2m \Omega \left[ V_0\sin(\lambda-\alpha) + g t \cos\lambda \right] \vec{j} $$
La force de Coriolis est dirigée vers l’Est si l’on tire vers le Nord et cela indépendamment de l’hémisphère.
Donc la trajectoire du projectile M va développer une déviation vers l’Est (coordonnée $y$) par rapport à sa composante principale dans le plan Nord-Sud. Après 2 intégrations successives et prenant comme valeur initiale $(0,0)$ pour les coordonnées position et vitesse sur l’axe Est-West, la déviation selon cet axe évolue selon l’expression :
$$ y(t) = -\frac{1}{3}\Omega g \cos\lambda t^3 + \Omega \sin(\alpha-\lambda) t^2 $$
Voyons un peu l’ordre de grandeur d’une telle déviation au bout du trajet balistique. Si on essaye de maximiser la distance parcourue nous savons que la direction de la vitesse initiale (en absence de prise au vent) est $\alpha = \pi/4$, de plus à nos latitudes on a aussi $\lambda \approx \pi/4$ donc le second terme est négligeable et il vient :
$$ \Delta y_{Est} \approx \frac{1}{3\sqrt{2}}\Omega g t_{vol}^3 = \frac{\Omega V_0^3}{12 g^2} $$
Numériquement, le produit $g \Omega \approx 7\ 10^{-4}\ m.s^{-3}$, donc un temps de vol de l’ordre de 1 seconde induise une déviation de 0.16 mm, par contre la puissance cubique du temps fait que pour une flèche allant à 100 m/s (environ 300 fps donc rapide) au bout des 500 m de trajectoire (cf. $x_{vol}$) alors le temps de vol est de 7 sec et donc la déviation de 55 mm !.
Conclusion
Dans cet article qui s’est voulu un peu exhaustif pour mes lecteurs curieux j’ai revisité les hypothèses dans lesquelles j’avais travaillé pour écrire mes articles sur la balistique des flèches : que fait la rotation de la Terre ? Elle induit primo un effet de déviation de la direction (et de l’intensité) de la pesanteur locale par rapport à la verticale, et donne naissance à une force inertielle dite de Coriolis du nom du mathématicien et ingénieur français Gaspard-Gustave Coriolis (1792-1843). C’est cette force qui peut en balistique faire rater sa cible.
On remarque que la déviation ne dépend pas explicitement de la masse de l’objet seul compte le temps de vol. Pour des applications militaires où les projectiles ont des vitesses initiales de l’ordre de 1000 km/s et des temps de vols de 20sec environ alors la déviation et de l’ordre de 1 à 2 mètres donc les artificiers doivent en tenir compte. Pour nos applications de tir à l’arc, en FITA avec des cibles à 50m ou même 70m le temps de vol est de l’ordre de la seconde et la déviation est négligeable. Elle ne le serait plus si on devait faire des tirs à plusieurs centaines de mètre avec 1 seule flèche car alors le temps de vol serait 7 à 10 fois supérieur. Pourquoi 1 flèche ? et bien si on dispose de plusieurs flèches alors le réglage du viseur servirait à compenser la dite déviation et nous serions sauvé !!!
Donc on peut l’oublier en pratique pour le TAA mais pas pour la météo car c’est elle qui est responsable des beaux enroulements de nuages autour des dépressions….