Introduction
En discipline de parcours (Campagne, Nature, 3D), il arrive fréquemment que les cibles soient placées soit en hauteur soit en dévers. Outre le fait que l’abaque doit être corrigée par rapport à un tir sur terrain plat (voir article art) il faut faire en sorte que le matériel n’induise pas de biais. Dans cet article je vais donner la raison pour laquelle on doit régler ce que l’on appelle le 3eme axe du viseur.
Les axes du viseur
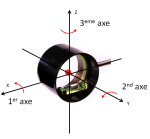
On parle ici du 3eme axe du viseur mais avant d’en parler pourquoi est-ce le 3eme ? En fait il s’agit en premier lieu d’orienter dans l’espace le scope qui est notre guide dans la visée. Or orienter le scope se fait via des rotations autour de 3 axes orthogonaux que l’on peut matérialiser comme sur l’image suivante.

Le premier axe concerne la bascule avant-arrière du scope, le second axe la rotation autour de son axe de symétrie, et le troisième axe l’orientation du scope dans le plan qui contient les deux premiers axes et qui passe par le centre de la lentille.
Le réglage du troisième axe
Le scope n’est pas flottant dans l’espace mais il est fixé sur le viseur lequel est lui-même fixé sur la fenêtre d’arc. C’est donc par l’intermédiaire des réglages du viseur que l’accède à ceux du scope. Par exemple voici sur mon SureLoc décrit dans cet article Viseur SureLoc Icon les réglages du 2e et 3e axes. Le 2nd axe fait pivoter la partie avant autour de l’axe de la partie arrière du viseur, le 3e axe fait pivoter la tête du viseur selon un axe perpendiculaire à la figure. On voit dans les deux cas les graduations et les vis de réglages. Il y a 2 vis de fixation sous le viseur à desserrer avant le réglage et à resserrer à la fin du réglage.

Maintenant une remarque utile : on peut ajuster l’orientation ‘viseur-scope’ indépendamment de l’arc. C’est plus pratique et tout à fait justifier car les poignées actuelles sont réalisées par des machines à commande numérique dont la précision mécanique est largement suffisante. D’autre part la poignée de l’arc ne présente pas forcément de logement ad equa pour fixer de manière sûre les niveaux à bulle. En fait il faut être certain que les niveaux à bulle soient perpendiculaires au plan dans lequel s’inscrit la fixation du viseur sur la fenêtre d’arc. C’est loin d’être évident à faire et on peut engendrer un défaut (biais) si les niveaux ne sont pas bien fixés : on sur ou sous corrigerait un 3e axe !
La méthode développée dans ce site dédié à la chasse me parait bien. Il s’agit de préparer un niveau de chantier assez grand muni par construction de 2 niveaux à bulle pour s’assurer de sa verticalité après fixation dans un étau par exemple. La fabrication du niveau assure la perpendicularité de l’axe des niveaux à bulle par rapport à un des côtés du niveau, ce dernier étant dans l’axe vertical après réglage de sa fixation dans l’étau.
Une fois le niveau bien étalonné, on se retrouve dans la situation schématisée ci-dessous, à savoir que l’axe x (des niveaux à bulle) est bien horizontal perpendiculaire à la verticale (fil à plomb) de l’axe z. On peut alors placer la barre d’extension de son viseur sur un des cotés du niveau et le faire pivoter vers le haut et vers le bas. Il est vraisemblable que la bulle du scope se mette à bouger dans un sens dans le mouvement vers le haut, et dans l’autre sens pour le mouvement vers le bas. Dans ces conditions on a besoin de régler le 3e axe !
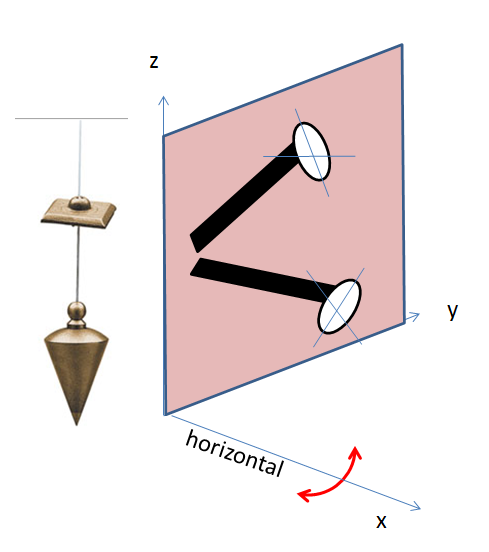
En fait cela est du à une propriété géométrique, dans la rotation autour de l’axe x, la seule configuration pour laquelle le niveau de scope ne bouge pas est celle pour laquelle il décrit la surface d’un cylindre d’axe de symétrie « x », sinon il se retrouve en fait sur la surface d’un cône d’axe « x » et donc se retrouve dans soit dans une orientation vers le haut soit l’orientation inverse vers le bas (et tout dépend si le cône à sa pointe coté x>0 ou x<0). Algébriquement on peut voir cela de la façon suivante.
L’axe du niveau à bulle su scope peut être matérialisé par un vecteur $\vec{v}$ qui peut se décomposer selon la base xyz selon des cosinus directeurs :
$$ \vec{v} = \cos \alpha_1 \vec{x} + \cos \alpha_2 \vec{y} + \cos \alpha_3 \vec{z} $$
Une rotation quelle conque d’angle $\theta$ autour de l’axe x s’écrit sous forme matricielle selon
$$ R(\theta) = \left( \begin{tabular}{ccc} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{tabular} \right) $$
Donc quand on opère une rotation $R(\theta)$ le vecteur $\vec{v}$ se transforme en un vecteur $\vec{w}$ de coordonnées données par la multiplication matricelle
$$ \vec{w} = R(\theta) . \vec{v} = \left( \begin{tabular}{ccc} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{tabular} \right) \left( \begin{tabular}{c} \cos \alpha_1 \\ \cos \alpha_2 \\ \cos \alpha_3 \end{tabular} \right) = \left( \begin{tabular}{c} \cos \alpha_1 \\ \cos \theta \cos \alpha_2 -\sin \theta \cos \alpha_3 \\ \sin \theta \cos \alpha_2 + \cos \theta \cos \alpha_3 \end{tabular} \right) $$
On veut que dans cette opération de rotation la bulle reste horizontale donc que $\vec{w}$ soit perpendiculaire à $\vec{z}$ donc cela signifie que la 3e composante de $\vec{w}$ est nulle quelque soit l’angle $\theta$. Soit
$$ sin \theta \cos \alpha_2 + \cos \theta \cos \alpha_3 = 0 $$
Premièrement, pour $\theta = 0$ cela signifie que $\cos\alpha_3 = 0$ or cela est acquis au moins s’en assure-t’on par le réglage du 2nd axe du viseur. Donc reste une fois ce second axe réglé, la condition
$$ \cos \alpha_2 = 0 $$
Ce qui signifie que l’angle entre l’axe y, matérialisant la direction de la l’extension du viseur, et l’axe du scope soit de 90°. C’est par le biais du réglage du 3e axe du viseur que l’on réalise cette condition.
Version vidéo (langue anglaise)
Merci Gilles.