Introduction
Face à un trispot en salle à 18m ou bien une cible avec 4 blasons à 50m, on se demande s’il faut retoucher son réglage pour atteindre les centres des spots. Dans cet article, on va donner la réponse dans le contexte d’une trajectoire balistique de la flèche.
Développement
J’utilise la relation (1) de l’article Réglages viseurs en parcours : petites et grandes distances (à plat)
à savoir la relation qui donne l’angle initial de la flèche (par rapport à l’horizontale).
$$ \frac{\tan \theta_F}{\tan\theta_0} = 1 - \frac{x_F}{x_F^{max}\sin 2\theta_0} \quad(1) $$
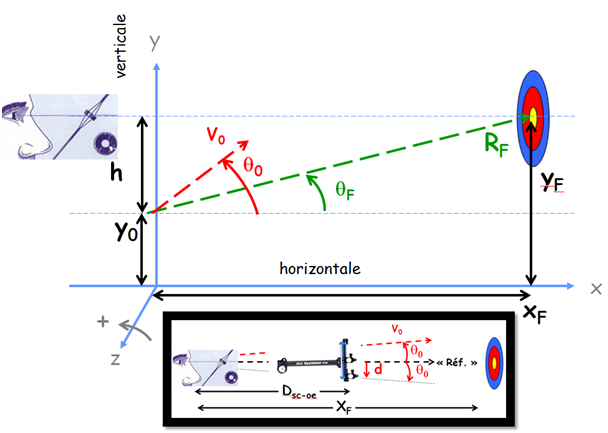
En fait $\tan[\theta_F]$ est par définition égal à $(Y_F -Y_0)/X_F$ (voir le schéma du même article reproduit ci-dessus) avec $Y_F$ l’altitude du centre du sport visé, $Y_0$ l’altitude de la flèche au départ, et $X_F$ la distance horizontale à la cible (par ex. 18m ou 50m).
Donc schématiquement $\theta_0$ est une fonction des variables $(Y_F, Y_0, X_F, v_0)$.
On note $\theta_{0r}$ la valeur de cet angle pour que l’archer envoie sa flèche au centre du spot de référence (cf. spot du milieu pour un tri-spot, ou bien le spot du bas pour une cible FITA 50m).
Maintenant supposons que l’archer utilise le même réglage mais pour viser un spot positionné à $Y_F + \delta Y$. La question est de savoir de combien il va rater le centre du spot.
Il faut pour cela se souvenir de l’équation de la trajectoire de la flèche, Eq. 18 Dynamique d’une fléche en phase de vol (Partie I) :
$$ Y = Y_0 + \tan \theta_0 X - \frac{1}{2} \frac{g}{v_0^2\cos^2\theta_0} X^2 $$
Alors l’écart $\Delta Y = Y_{spot} - Y_{true}$ entre la position du nouveau spot et la position vraiment atteinte est égale à
$$ \Delta Y = Y_F + \delta Y - \left( Y_0 + \tan \theta_{0r} X_F - \frac{1}{2} \frac{g}{v_0^2\cos^2\theta_{0r}} X_F^2 \right) $$
(ici $g = 9.81 m/s^2$, les distances en mètre et la vitesse en m/s)
Cas pratiques
Les deux cas que l’on peut étudier sont par exemple :
- l’effet de passer du spot central (référence) au spot du haut ou du bas pour un blason tri-spot placé à 18m
- -# l’effet de passer du blason du bas à celui du haut pour une cible FITA 50m 2x2 balsons, ou bien vice versa.
Dans ces deux cas, je considère que la flèche est placée à $Y_0 = 1.50m$ (valeur typique). Je rappelle également que pour un tri-spot le spot central est placé à une hauteur de 1.30m et le spot du haut (ou du bas) est distant de 22cm par rapport à cette référence. Dans le cas d’une cible FITA 2x2 blasons, le centre du blason du bas est à une hauteur de 1.11m et celui du haut est déplacé de 50cm.
Voici les résultats numériques (notez que ce sont des mm pour l’axe vertical) en fonction de la vitesse initiale de la flèche en unité f.p.s
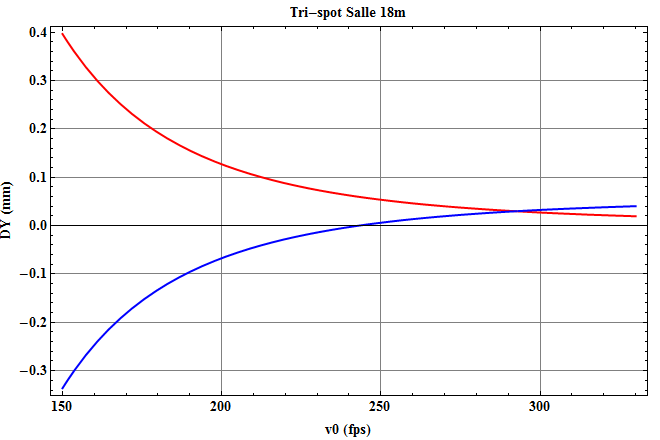
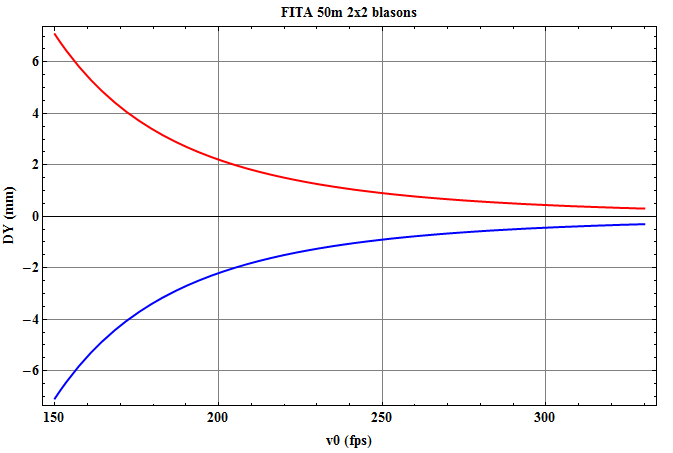
Les courbes rouges valent pour un déplacement vertical vers le haut du spot déplacé par rapport au spot de référence, tandis que pour les courbes bleues on déplace le spot vers le bas. *
Notez que dans les 2 configurations étudiées et pour des valeurs raisonnables de vitesses, l’erreur due à la balistique que fait l’archer en ne changeant pas de réglage de viseur est bien négligeable.. C’est le résultat principal de cet article.
Pour les esprits curieux la non symétrie entre la courbe rouge et la courbe bleue à 18m vient de la hauteur initiale de la flèche. A 50m cette hauteur a pratiquement pas d’influence.
Maintenant, il y a d’autres facteurs qui pourrait influencer la perte/gain de trait quand on passe d’un spot de référence à un autre spot. En salle on pourrait être influencé par la luminosité suivant le type et la disposition de l’éclairage. A 50m on pourrait se demander si le vent influe sur les trajectoires différentes. Également, à 50m le corps va être mis en posture légèrement différente en visant le blason du haut ou du bas, donc la sensation neuro-sensorielle peut être influencée.
Donc dans un premier temps ce n’est pas la balistique pure qui va faire faire des erreurs, ensuite il faut s’adapter.