Introduction

Révision de la discussion le 19/9/12

Cet article est le troisième chapitre sur l’étude des oscillations d’une corde vibrante lestée avec des masselottes.

Dans le premier chapitre (cf. Oscillations de la corde (Partie I)) j’ai établi l’équation de la corde vibrante et étudié l’évolution d’une corde pincée non lestée. Le résultat principal est que la partie centrale de la corde lâchée sans vitesse se déplace à vitesse constante.

Dans le second chapitre (cf. Oscillations de la corde avec masselotte centrale (Partie II)), j’ai d’abord étudié comment est modifiée l’équation de la corde vibrante ainsi que les conditions aux limites dans le cas de masselottes ponctuelles. Puis après avoir placé une masselotte de poids identique à une flèche de 300 grains, j’ai montré que la corde pincée et lâchée sans vitesse se déplace en un mouvement accéléré jusqu’à sa position de repos où elle acquière sa vitesse maximale. Une application numérique a rendu compte du temps de propulsion et de la vitesse d’éjection typiques obtenus lors d’une étude dynamique de la phase de propulsion (cf Dynamique (simple) d’une fléche en phase de propulsion).

Dans ce troisième chapitre, je vais aborder le cas où sont rajoutées 2 petites masselottes proches symétriquement des bords en plus de la masselotte centrale rendant toujours compte du poids de la flèche. On a pour résumé :

• une corde de masse $mc$ et de longueur $L$ soumise à une tension constante $T$
• une masselotte positionnée en $L/2$ de masse $M$
• deux masselottes de masse $m$ positionnées en $\xi$ et $L-\xi$ avec $0 < \xi < L/2$ bien en tendu.

Et l’on veut connaître la vitesse lorsque la corde revient à sa position de repos après avoir été lâchée sans vitesse depuis une position initiale en forme triangle de hauteur $H$ représentative du lâché de corde après une phase d’armement.

Equations et résolutions

Définitions des fonctions propres et expressions des contraintes

La résolution du problème à 3 masselottes suit en tous points celle rencontrée au chapitre II et j’invite le lecteur à se rafraichir la mémoire avant d’entamer ce qui suit. La Figure 1 fixe les idées et les notations employées.

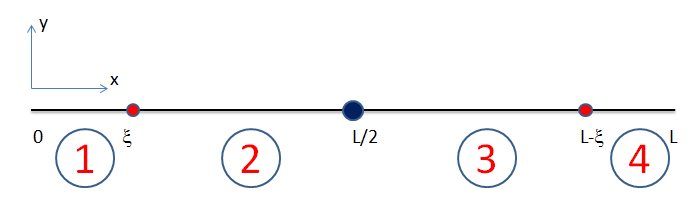
Figure 1 Notations : la corde est attachée aux extrémités en $x=0$ et $x=L$, les masselottes sont aux positions $x=\{\xi, L/2, L-\xi\}$, et les solutions représentant des états de vibrations de la corde sont indicées par $i=1,2,3,4$ selon la partie de la corde concernée.
La corde est virtuellement découpée en 4 parties avec aux extrémités de chaque partie soit une masselotte soit un point fixe (les 2 points d’attache de la corde). Les états propres de vibrations (ou modes) $\Phi_i(x)$ que nous avons rencontrés au chapitre II sont indicés par $i=1,2,3,4$ selon la portion de corde concernée. L’état propre global $\Phi(x)$ n’est que la collection des différents $\Phi_i(x)$. Nous avons établi au chapitre II que ces fonctions sont assujetties à toute une série de contraintes de continuité de positions d’une part et d’éventuelles discontinuité de pente d’autre part à chaque extrémité des 4 parties précitées. Donc, elles satisfont le système d’équations suivant :

$$ \begin{array}{rclr} \Phi_1(0) &= &0 = \Phi_4(L) &(Eq.1-1)\\ \Phi_1(\xi) &=&\Phi_2(\xi) & (Eq.1-2) \\ \Phi_2(L/2)&=&\Phi_3(L/2) &(Eq.1-3) \\ \Phi_3(L-\xi) &=&\Phi_4(L-\xi) &(Eq.1-4)\\ T\left(\Phi_2^{\prime}(\xi)- \Phi_1^{\prime}(\xi )\right) &=& - \frac{m \omega^2}{2} \left(\Phi_1(\xi)+\Phi_2(\xi)\right) &(Eq.1-5) \\ T\left(\Phi_3^{\prime}(L/2)- \Phi_2^{\prime}(L/2)\right) &=& - \frac{M \omega^2}{2} \left(\Phi_2(L/2)+\Phi_3(L/2)\right) &(Eq.1-6) \\ T\left(\Phi_4^{\prime}(L-\xi)- \Phi_3^{\prime}(L-\xi )\right) &=& - \frac{m \omega^2}{2} \left(\Phi_3(L-\xi)+\Phi_4(L-\xi)\right) &(Eq.1-7) \end{array} $$

Les 4 premières équations sont les contraintes de continuité de position, tandis que les 4 suivantes concernent les pentes à gauche et à droite au niveau des masselottes. Pour ces dernières j’ai utilisé les contraintes de continuité pour écrire une forme symétrique des membres de droites. La pulsation $\omega$ est toujours reliée au vecteur d’onde $k$ par l’expression de dispersion linéaire $k = \omega\ c$ avec $c$ la vitesse de propagation le long de la corde donnée par $c^2 = (T\ L)/mc$.

Je rappelle que toutes les fonctions $\Phi_i(x)$ peuvent se mettre sous l’une ou l’autre des formes génériques suivantes (je laisse au lecteur le soin d’établir les relations entre les coefficients) :

$$ A\sin(k x) + B \cos(k x) = A^{\prime} \sin(k x+\phi) + B^{\prime} \cos(k x+\phi) $$

En utilisant les Eq.1-1 et Eq.1-3 on peut d’une manière générale chercher les solutions $\Phi_1$, $\Phi_2$, $\Phi_3$ et $\Phi_4$ à l’aide de 5 constantes $A_j$ ( $j=1,\dots,5$) selon :

$$ \begin{array}{rclr} \Phi_1(x)& =& A_1 \sin k x & (Eq.2-1)\\ \Phi_2(x)& =& A_2 \sin k(x-L/2) + A_3 \cos k(x-L/2) &(Eq.2-2)\\ \Phi_3(x)& =& A_4 \sin k(x-L/2) + A_3 \cos k(x-L/2) &(Eq.2-3)\\ \Phi_4(x)& =& A_5 \sin k(x-L) & (Eq.2-4) \end{array} $$

Système d’équations des variables

En reportant les expressions des différentes fonctions $\Phi_i$ (Eq.2-1 à Eq. 2-4) dans le système Eq.1-1 à Eq.1-7, on obtient un système homogène de 5 équations à 5 inconnues que l’on peut mettre sous la forme compacte suivante :

$$ \begin{array}{rcl} \alpha_1 A_1 + \alpha_2 A_2 + \alpha_3 A_3 &=& 0 \quad\quad (Eq.3-1)\\ \gamma_1 A_1 + \gamma_2 A_2 + \gamma_3 A_3 &=& 0 \quad\quad (Eq.3-2)\\ \beta_3 A_3 + \beta_4 A_4 + \beta_5 A_5 &=& 0 \quad\quad (Eq.3-3)\\ \epsilon_3 A_3 + \epsilon_4 A_4 + \epsilon_5 A_5 &=& 0 \quad\quad (Eq.3-4)\\ \delta_2 A_2 + \delta_3 A_3 + \delta_4 A_4 &=& 0 \quad\quad (Eq.3-5) \end{array} $$

Les coefficients du système ont les expressions suivantes (Eq.4) :

$$ \begin{array}{rcl} \alpha_1 & = & \sin k \xi\\ \alpha_2 & = & \sin k (L/2 - \xi)\\ \alpha_3& = & -\cos k (L/2 - \xi)\\ \beta_3 & = & \alpha_3\\ \beta_4 & = & -\alpha_2\\ \beta_5 & = & -\alpha_1 \\ \gamma_1 & = & \cos k \xi - \frac{p_1}{2} \sin k \xi \\ \gamma_2 & = & - \cos k (L/2 - \xi) + \frac{p_1}{2}\sin k (L/2 - \xi)\\ \gamma_3 & = & - \sin k (L/2 - \xi) + \frac{p_1}{2}\cos k (L/2 - \xi)\\ \epsilon_3 & = & -\gamma_3\\ \epsilon_4 & = & \gamma_2\\ \epsilon_5 & = & \gamma_1\\ \delta_2 & = & 1 \\ \delta_3 & =& - p_0\\ \delta_4 & = & -1 \end{array} $$

où j’ai utilisé les notations suivantes.

$$ \begin{array}{rcccl} p_0 &=& \frac{M \omega^2}{T k}& =& \frac{M}{mc} (k L) \\ p_1 &=& \frac{m \omega^2}{T k}& =& \frac{m}{mc} (k L) \\ \end{array} $$

Résolution

Le système des Eq.3 étant homogène, une solution non triviale (cf. tous les coefficients nuls !) est possible si un certain nombre de coefficients dépendent des autres (le déterminant global est nul dans ce cas). On remarque que dans toutes les équations Eq.3 la présence de la variable $A_3$ ce qui nous donne une piste.

En multipliant Eq.3-1 par $\gamma_2$ et Eq.3-2 par $\alpha_2$ on obtient la relation entre $A_1$ et $A_3$ suivante :

$$ \delta A_1 + \delta^{\prime} A_3 = 0 \quad\quad Eq.5 $$

avec

$$ \begin{array}{rcl} \delta &=& \alpha_1 \gamma_2 - \alpha_2 \gamma_1 \\ \delta^{\prime} &=& \gamma_2 \alpha_3 - \alpha_2 \gamma_3 = 1 \end{array} $$

La dernière égalité est facile à démontrer avec les relations Eq.4.

Donc de deux choses l’une soit $\delta = 0$ soit $\delta \neq 0$.

Les modes impaires

Prenons le cas $\delta = 0$, on en déduit immédiatement d’après Eq.5 que $A_3 = 0$. Alors en reportant dans le système Eq.3, il vient naturellement (Eq.6) :

$$ \begin{array}{rcl} \alpha_1 A_1 + \alpha_2 A_2 &=& 0\\ \alpha_2 A_2 + \alpha_1 A_5 &=& 0\\ A_2 &=& A_4 \end{array} $$

Deux nouveaux cas de figure se présentent selon que $\alpha_1 = 0$ ou bien $\alpha_1 \neq 0$. Les cas de la nullité ou non de $\alpha_2$ sont directement liés à ceux de $\alpha_1$ car je rappelle qu’ici on discute dans le cadre où $\delta = 0$.

Donc si $\alpha_1 \neq 0$ (et par voie de conséquence $\alpha_2\neq 0$) alors :

$$ \begin{array}{rclc} \Phi_1(x) &=& A \sin k x &\quad (0,\xi) \\ \Phi_2(x) &=& -A\frac{\sin k\xi }{\sin k(L/2-\xi)} \sin k (x-L/2) &\quad (\xi,L-\xi) \\ \Phi_4(x) &=& A \sin k (x-L) &\quad (L-\xi,L) \end{array} $$

La fonction $\Phi_3$ (Eq.2-3) étant identique à la fonction $\Phi_2$ j’ai étendu le domaine de validité de cette dernière. Cet ensemble de fonctions est impair par rapport à la position centrale $L/2$ (cf. changement de signe), la tangente est continue en $L/2$ par contre la tangente est discontinue en $\xi$ et $L-\xi$.

Si $\alpha_1 = 0$ alors $\alpha_2 = 0$ (cf. imposé par $\delta=0$), et $\gamma_1 = \pm 1$ ainsi que $\gamma_2 = \pm 1$. Dans ce cas :

$$ \begin{array}{rclc} \Phi_1(x) &=& -A\frac{\gamma_2}{\gamma_1} \sin k x &\quad (0,\xi) \\ \Phi_2(x) &=& A\sin k (x-L/2) &\quad (\xi,L-\xi) \\ \Phi_4(x) &=& - A\frac{\gamma_2}{\gamma_1} \sin k (x-L) &\quad (L-\xi,L) \end{array} $$

De même l’ensemble de ces fonctions est impair par rapport à la position centrale. De plus $k \neq 0$ que si $\xi$ satisfait la relation :

$$ \frac{\xi}{L} = \frac{n}{2(n+m)} \quad\quad n,\ m = 1,\ 2,\ 3,\ \dots $$

Les deux ensembles de solutions donnent des fonctions impaires par rapport à la position centrale. Or nous avons vu dans le chapitre II que les coefficients de décomposition de la fonction $u(x,t)$ décrivant l’évolution de la corde au cours du temps, dépendent de la parité de la fonction $f(x)$ donnant la position à l’instant $t=0$. Si $f(x)$ est paire comme dans le cas d’une corde pincée en son milieu représentant l’état de la corde à pleine allonge, alors les modes impairs ne sont pas excités. Nous pouvons les oublier pour la suite de ce chapitre.

Les modes paires

Dans ce cas de figure $\delta \neq 0$ alors la résolution du système Eq.3 donne (Eq.7) :

$$ \begin{array}{rclc} \Phi_1(x) &=& -A \sin k x &\quad (0,\xi) \\ \Phi_2(x) &=& -A \delta^{\prime\prime}\sin k(x-L/2) + A \delta\cos k(x-L/2) & (\xi,L/2)\\ \Phi_3(x) &=& A \delta^{\prime\prime}\sin k(x-L/2) + A \delta\cos k(x-L/2)& (L/2,L-\xi) \\ \Phi_4(x) &=& A\sin k(x-L/2) & (L-\xi,L) \end{array} $$

(en fait on a redéfinit $A_3/\delta$ en $A$). On constate que ce système de fonctions est pair et de tangente discontinue pour la position centrale. La discontinuité de la tangente aux autres positions de masselottes est sujette à des contraintes sur $k$.

Par ailleurs, l’équation Eq.3-5 devient une contrainte à laquelle doit satisfaire de toute façon $k$, à savoir :

$$ \delta_3 \delta - 2\delta^{\prime\prime} = 0 $$

ou

$$ \delta_3 (\alpha_1\gamma_2-\alpha_2\gamma_1) - 2(\alpha_1\gamma_3-\alpha_3\gamma_1) = 0 $$

qui devient en exploitant les définitions des coefficients $\alpha_i$ et $\gamma_i$ (Eq.8) :

$$ \begin{align*} -* 2 \cos k\frac{L}{2} &+ \frac{k L M}{mc}\sin k \frac{L}{2} \\ & + \left[ 2\cos k\left(\frac{L}{2}-\xi\right)-\frac{k L M}{mc}\sin k\left(\frac{L}{2}-\xi\right)\right] \frac{k L m}{mc} \sin k\xi = 0 \end{align*} $$

Nous avons déjà vu ce genre d’équation transcendantale lors du chapitre II, elle ne peut se résoudre que numériquement et donc dans le cas où l’on fixe les valeurs des autres paramètres du problème (masses, longueur de la corde, position des masselottes latérales). Ceci dit une fois fixé ces paramètres, on obtient un spectre discret de valeur de $k$ que l’on peut indicé selon $k_n$ avec $n=1,2,\dots$.

Notons enfin pour clore cette section qu’étant donné la parité du système Eq.7, ce sont ces solutions qui nous importerons dans la suite.

Comme dans le cas étudié dans le chapitre II, l’évolution de la forme de la corde est donc donnée par le développement :

$$ u(x,t) = \sum_{n=1}^{\infty} C_n \Phi_n(x)\cos(c k_n t + \phi_n) $$

(Attention : l’indice de $\Phi$ ici correspond à une solution de Eq. 7 définie pour une valeur de $k=k_n$ du spectre solution de Eq.8)

De même la distribution des vitesses le long de la corde est donnée par l’expression :

$$ v(x,t) = -c \sum_{n=1}^{\infty} C_n k_n \Phi_n(x)\sin(c k_n t) $$

(le signe $-$ est purement du à l’orientation de l’axe vertical)

La vitesse initiale prise nulle partout cela fixe $\phi_n = 0$ pour tout $n$. La forme initiale $f(x)$ de la corde se décompose selon

$$ f(x) = \sum_{n=1}^{\infty} C_n \Phi_n(x) $$

ce qui fixe les valeurs des coefficients $C_n$ part

$$ \begin{array}{rl} C_n = \left[ \int_0^L f(x) \Phi_n(x)\ mc\ dx/L \right.& + m f(\xi)\Phi_n(\xi) \\ + m f(L-\xi)\Phi_n(L-\xi) &\left.+ M f(L/2) \Phi_n(L/2) \right] \times \frac{1}{\||\Phi_n\||^2} \end{array} $$

($\||\Phi_n\||^2$ n’est autre que l’expression du numérateur de $C_n$ où $f(x)$ est remplacé pas $\Phi_n$).

Etude d’un cas particulier

Dans ce qui suit je vais étudier quelques cas particuliers pour cerner le problème et à la fin je ferai appel à un programme de minimisation même si je resterai non exhaustif.

Prenons comme paramètres de base :

• une corde de longueur $L=1$m et de masse $mc=75$grains ($\approx 5$g) ;
• une masse $M = 4mc =300$grains représentative de la flèche positionnée au milieu de la corde ;
• deux masselottes $m =0.4 mc= 0$grains situées à une distance $\xi=L/20$ des extrémités.

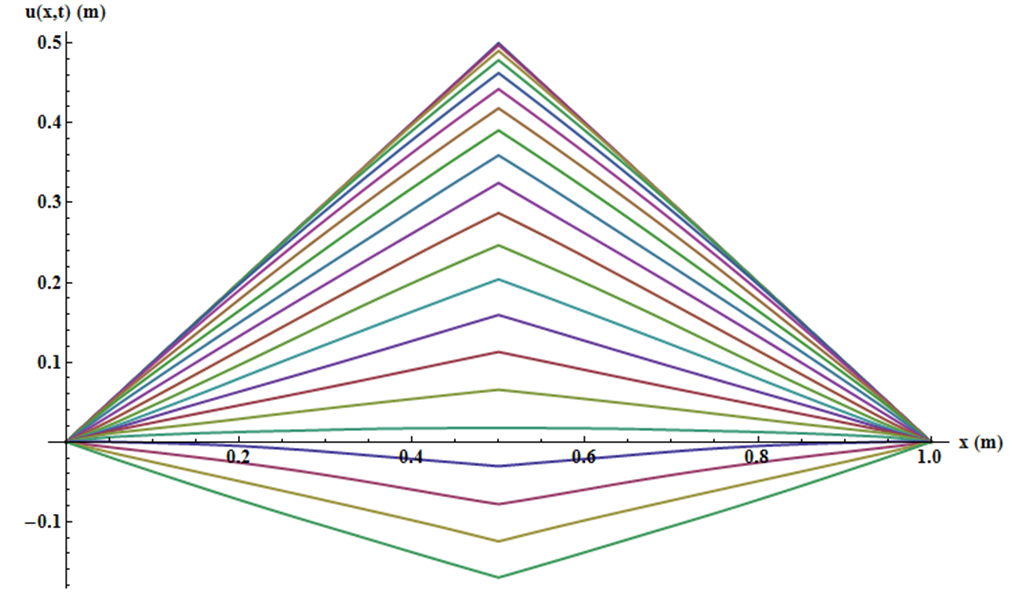
La corde est lâchée sans vitesse dans une position « triangulaire » d’une hauteur $H=L/2$ représentative d’une décoche à pleine allonge. L’évolution de sa forme est donnée sur la Fig.2 où les « flashes » sont pris à intervalles réguliers d’unité $1/10 L/c$ soit environ toutes les $0.6$ms (millième de seconde) avec $c = \sqrt{T L/mc}\approx 176$m/s pour une tension de 35lbs (50lbs de puissance pic, voir la fin du chapitre II pour la discussion à ce sujet).

Figure 2 : Evolution de la forme de la corde avec des masselottes latérales de 30 grains ($0.4 mc$) et une masselotte centrale représentant la flèche de 300 grains.
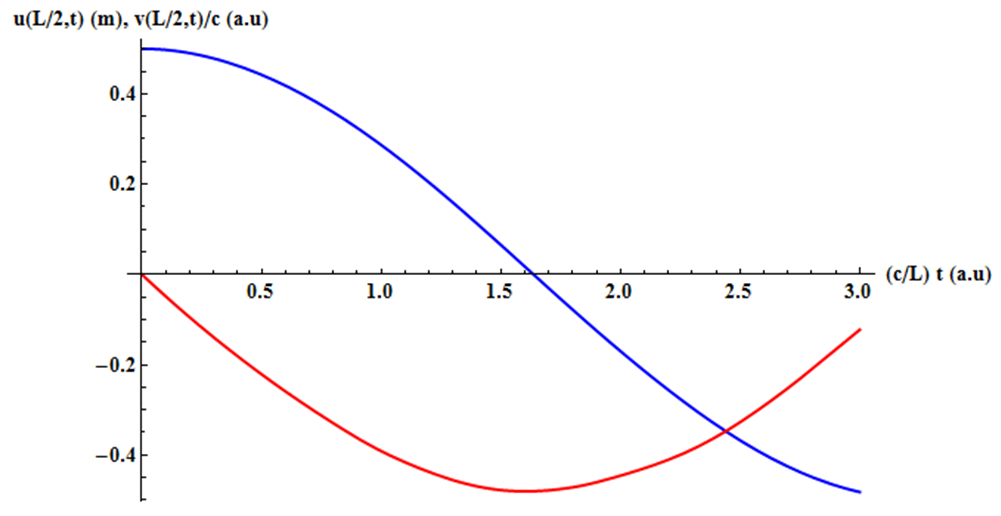
Si on se concentre sur l’évolution de la position et de la vitesse au centre de la corde où se situe la masselotte de 300 grains représentant la flèche à propulser, nous obtenons le chronographe suivant (Fig.3) :

Figure 3 Evolution temporelle en unité de $c/L\approx 0.6$ms de la position (bleu) et de la vitesse (rouge), cette dernière exprimée en unité de $c\approx 176$m/s

Quand la partie centrale de la corde revient à sa position de repos ($u(L/2,t_{max})=0$) elle acquière sa vitesse maximale et en fait la flèche s’éjecte à ce moment là, et le modèle avec cette masselotte centrale ne peut rendre compte de ce qu’il se passe après éjection. Ceci dit au moment de l’éjection on a :

• $t_{max} = 1.6365 L/c \approx 9.3$ms
• $v_{max} = 0.4803 c \approx 84.5$m/s ou 277 fps.

Avec toutes choses égales par ailleurs sauf que l’on enlève les masselottes latérales on obtient :

• $t_{max} = 1.6354 L/c$
• $v_{max} = 0.4767 c$.

Donc en ayant mis des masselottes dans la configuration précédente on a gagné un peu de vitesse à savoir en valeur relative 0.75% ! soit à peine 2 fps…

Vous me direz que j’ai peut-être mal placé les masselottes et/ou mal choisi leur masse.

Prenons alors les mêmes masselottes de 30grains ($0.4 mc = 0.1 M$) et on les éloigne des extrémités en les plaçant à une distances de $\xi = 2\ L/20= L/10$. On constate alors que $v_{max} = 0.4827 c$ soit donc un gain de 3.4fps.

Ha ! fort de ce résultat on se dit repoussons encore nos masselottes en $\xi = 3\ L/20$. Le verdict tombe, la vitesse retombe à une valeur de $v_{max} = 0.4764 c$ soit à une valeur quasi identique à celle sans masselotte. On a donc mis en évidence le fait que le choix de la position des masselottes n’est pas anodine et qu’il y a sans doute un optimum.

Mettons nous à $\xi=L/10$ (même si ce n’est pas l’optimum global il l’est dans notre échantillonnage) et changeons la masse $m$. Prenons par exemple $m=3\ M/20 \approx 45$grains, on obtient alors $v_{max} = 0.4800 c$ qui ne présente pas de différence significative par rapport à des masselottes de $m=M/10$.

Essayons des masselottes plus légères à savoir $m=M/20\approx 15$grains… Le suspense est à son comble, on obtient $v_{max} = 0.4804 c$ modifiant là encore très marginalement.

Essayons des masselottes plus légères encore à savoir $m=M/30\approx 10$grains… On constate que $v_{max} = 0.4782 c$ et donc décroit vers la valeur obtenue sans masselotte. Donc, il faut des masselottes de poids raisonnable mais suffisant.

Je peux aller un peu plus loin en faisant appel à Mathematica, un logiciel (payant) de calcul symbolique et numérique. Sans donner les détails, voici le résultat de la variation de la vitesse centrale en fonction du poids des masselottes latérales et de leur position sur la corde (nb. je garde toute chose égale par ailleurs). Alors il y a bien un extremum de la vitesse pour $m = 0.103 M\approx 30$grains et $\xi = 0.092 L\approx 9.2$cm, et cela permet d’atteindre un accroissement de $3.5$fps. Ceci dit le maximum (minimum en fait à cause du signe « - ») n’est pas très « piqué » comme on peut le voir sur la représentation de la Fig.4.

Figure 4 Plot de l’évolution de la vitesse de la flèche (axe vertical) en fonction du poids des masselottes en fraction de ma masse de la flèche $m = \hat{m} M$ (axe de gauche) et de la position de ces masselottes en unité de longueur de la corde $\xi = \hat{\xi} L$ (axe de droite). La vitesse est exprimée en unité de $c$

Une représentation sous forme de courbes de niveau (Fig.5) permet de situé le minimum (maximum en valeur absolue) de la vitesse.

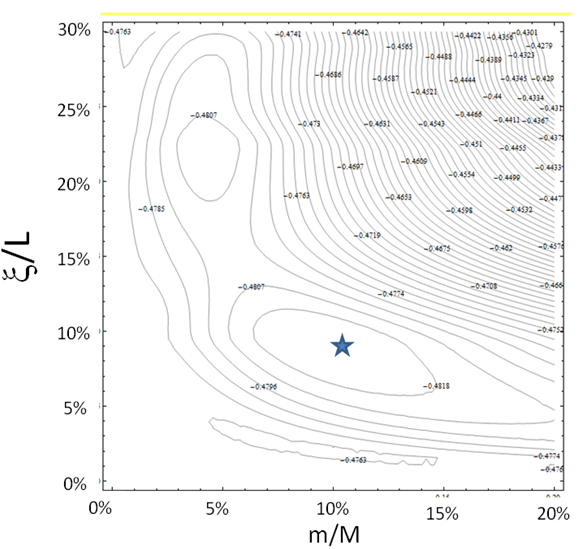
Figure 5 Courbes de niveau permettant de situer le minimum (maximum en valeur absolue) en fonction du poids des masselottes exprimée en pourcentage du poids de la flèche, et la poisition des masselottes par rapport aux extrémites de la corde exprimée en fonction de la longueur de celle-ci. Le maximum est de $v_{max}= 0.4829 c$, pour mémoire la vitesse obtenue sans masselottes est de $v_{max} = 0.4767 c$.

Discussion

Du cas particulier étudié dans la section précédente, j’en tire les enseignements suivants :

• il existe bien une configuration (masse, position) où l’ajout de masselottes latérales procure un incrément de vitesse ;
• l’incrément de vitesse maximal est cependant modeste dans cette configuration puisqu’il est de l’ordre de 1% de la vitesse sans masselotte soit d’environ 3fps. La question est de savoir s’il existe des configurations (puissance, longueur de corde, poids de flèche) où cet incrément est significatif

En regardant d’un peu plus près les équations des sections précédentes on s’aperçoit que la localisation du maximum de vitesse dans l’espace (masse, position) dépend de la longueur de la corde et de la masse de la flèche (en relatif par rapport à la masse totale de la corde) mais point de la tension de la corde (seul la valeur de $c$ en dépend).

Donc, tout changement de cordage dont la longueur ATA, de configuration Salle/extérieur avec des flèches de poids différents remets en question le choix des poids des masselottes et leur position…