Introduction
Dans les articles Faites sonner les flèches ! (Partie III), j’ai décrit la façon dont on peut « facilement » appréhender les oscillations de flexion des flèches selon la théorie d’Euler-Bernouilli. En fait, cette description théorique est approximative qui néglige les effets de cisaillement à savoir que lors de la flexion il y a déplacement des éléments de solides. Une théorie qui prend en compte ces effets de cisaillement est donnée par celle de Stephen Timoshenko (1878 Ukraine -1972 Allemagne). Mais dans le cas de « poutres » pour lesquelles la dimension transverse est petite devant la longueur (ex. le cas de nos flèches) en principe les descriptions d’Euler-Bernouilli et de Timoshenko donne des résultats équivalents.
Cependant, ayant testé que des ACEs, je m’interrogeais sur le fait que ces tubes étant profilés en principe la masse linéique aussi bien que la rigidité varient selon la position le long du tube. Bien qu’ayant fait un rapide calcul montrant que cet effet devait être négligeable dans nos cas pratiques, l’idée de tester des tubes cylindriques m’est germée naturellement. Ayant des RedLine de mes débuts sous la main de spine 690, j’en ai coupée une à 26.6in. Voici le résultat des mesures.
Mesures des fréquences d’une RedLine 690
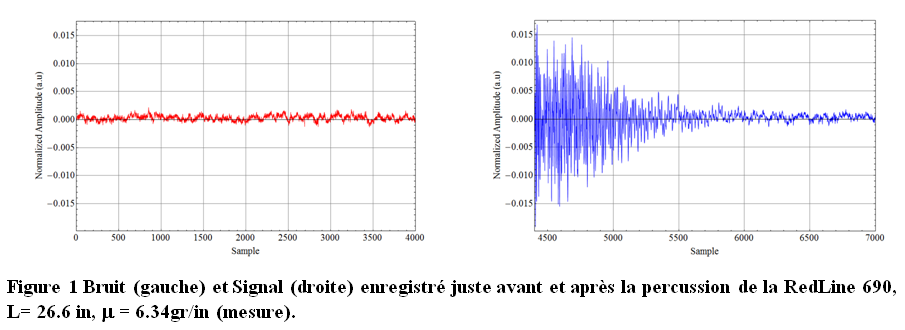
J’ai utilisé le même mode opératoire décrit dans Faites sonner les flèches ! (Partie III). Voici sur la Figure 1, les traces du « bruit » avant et le « signal » après la percussion de la flèche.
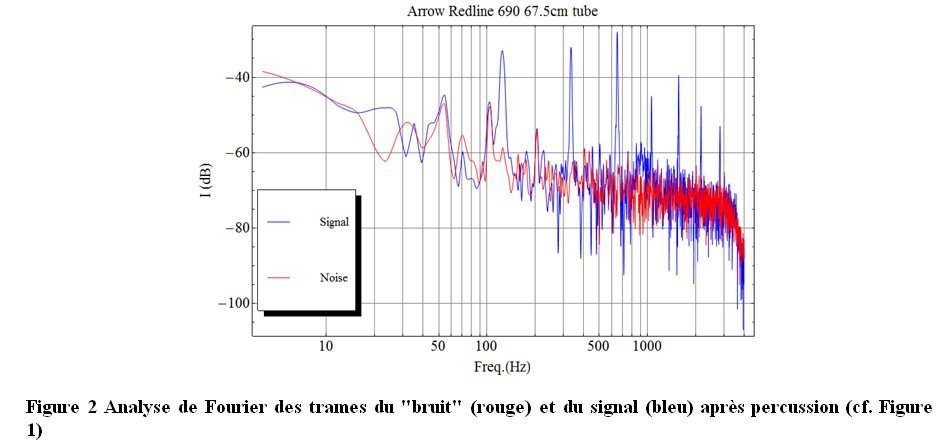
L’analyse de Fourier du bruit et du signal est présentée sur la Figure 2 et l’on remarque bien les pics caractéristiques de vibration de la RedLine (courbe bleue) qui sortent très nettement du bruit de fond ambiant (courbe rouge).
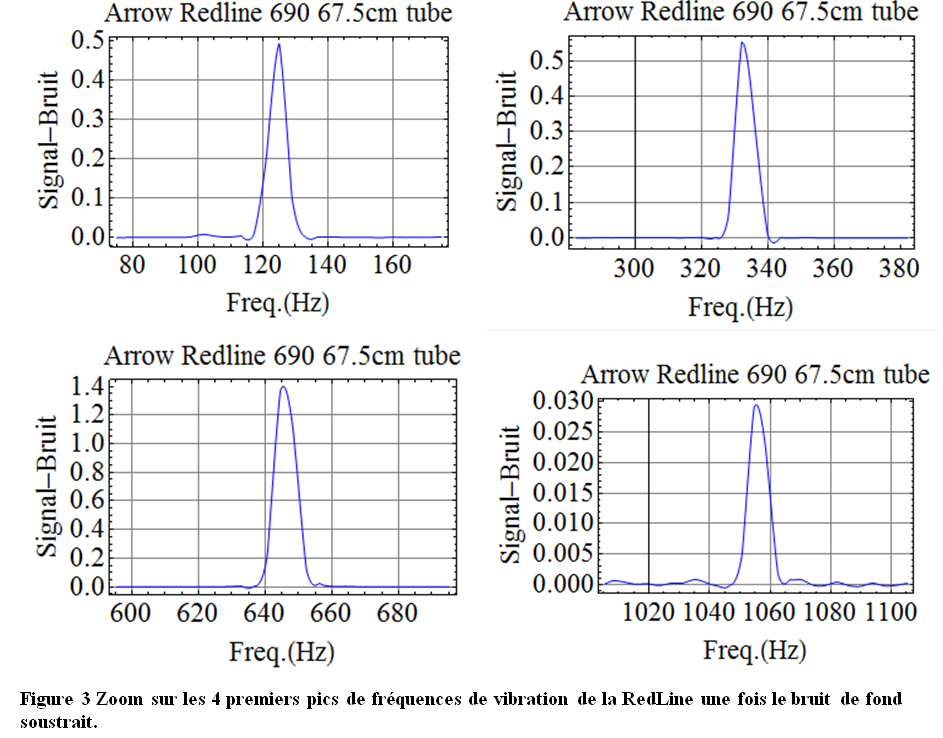
Les 4 premiers pics au-delà de 100Hz sont extraits par soustraction de la composante du bruit et l’on obtient :
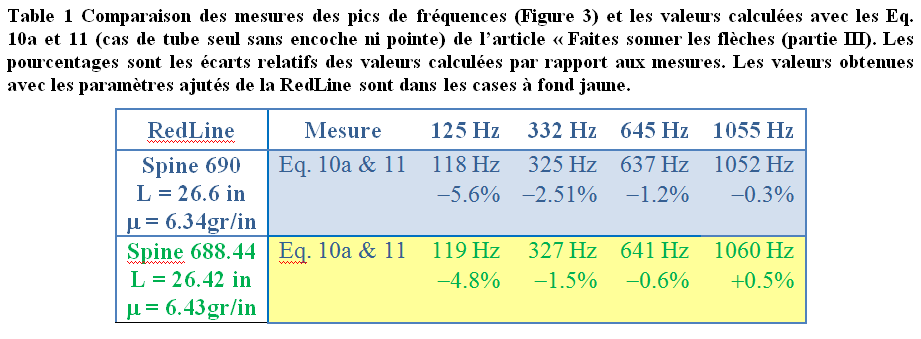
Dans la Table 1 sont reportées les 4 fréquences mise en évidence Figure 3. Si on utilise les valeurs des paramètres de la flèche tels qu’ils sont donnés par EASTON pour le spine (690) et les mesures directes sur la flèche (longueur et masse) alors on obtient un premier jeu de fréquences calculées à l’aide des formules Eq. 10a et 11 de l’article Faites sonner les flèches ! (Partie III). Si maintenant, on laisse libre ces trois paramètres pour ajuster au mieux les prédictions des fréquences aux mesures, alors :
- . Je trouve des valeurs de paramètres suivants de la RedLine :
- spine 688.44 au lieu de 690 : est-ce possible sachant que ces tubes ont 6 ans d’age sans avoir été conditionnés au mieux, et quand on dit « spine 690 » quel est la tolérance pour les RedLine qui n’ont/avaient pas les mêmes critères de fabrication que les ACEs ;
- L = 26.42in = 67.1cm : c’est 3mm de moins que la mesure qui elle est fiable à mieux que 1mm mais ce n’est pas complètement farfelu voire on peut se demander si ces 3mm ne sont pas à attribuer à la taille de la ligature qui permet de suspendre la flèche ;
- $\mu = 6.43gr/in$ : si on calcule la masse totale $\mu L = 169.9$gr au lieu de 168.4gr mesuré avec une balance Carbone Express de précision. Cela reste dans la marge de précision de la balance, donc cela semble acceptable bien que cette valeur est plus grande que celle mise dans la base de données de OnTarget pour cette flèche (cf. 6.27gr/in).
- Les fréquences calculées avec ces paramètres sont en général en meilleurs accords avec les mesures sauf la première fréquence qui ne changent pas vraiment.
Résumé et perspectives
Dans cet article, j’ai rendu compte des mesures des fréquences de vibration d’une flèche à tube de section constante (RedLine 690) pour lever le doute sur l’influence du profilage des ACEs utilisées dans l’article Faites sonner les flèches ! (Partie III).
Les calculs reportés dans la Table 1 montrent en premier lieu que les désaccords théorie/mesure avec ce type de flèche sont du même ordre de grandeur que ceux avec les ACEs, donc cela corrobore les estimations faites lors du précédent article montrant a priori le peu d’influence que pouvait engendrer la variation du profil de la flèche.
Ensuite, étant donné que cette flèche datait de ma première année de compétition, elle datait de plus de 5ans et donc je me demandais si ses caractéristiques avaient pu évoluées. Laissant libre les paramètres (spine, longueur, masse par unité de longueur) pour ajuster au mieux les fréquences calculées aux valeurs mesurées, j’ai obtenu des paramètres tout à fait plausible et un meilleur accord théorie/mesure. Seule la fréquence fondamentale ne bénéficie pas de l’amélioration globale avec un désaccord résiduel de -4.8% (-6Hz sur 125Hz mesuré).
On obtient donc s’en doute la limite de détermination des fréquences de vibration par cette méthode. Cependant à la lumière de la Table 1, on peut se poser la question de l’exacte valeur du spine et masse par unité de longueur des ACE utilisées dans les articles précédents.