Introduction
A la suite d’un problème posé par un étudiant en TIPE, j’ai trouvé intéressant de faire un petit point sur des raccourcis trompeurs. En l’espèce, l’étudiant trouvait paradoxal qu’un arc à poulies puissent être moins puissant qu’un arc classique considérant la même allonge et la même puissance pic.
Pour bien suivre, j’invite le lecteur à passer quelques minutes sur l’article Dynamique (simple) d’une fléche en phase de propulsion.
Le problème
Pour bien comprendre le dilemme face auquel on peut être confronté, prenons l’exemple du résultat que donne l’EASTON Shaft selector (j’ai encore la version 2006 qui était téléchargeable) : pour une allonge de 28in et une puissance maximale pour un arc classique ou pic pour un arc à poulies de 42lbs, le programme préconise l’emploi d’une flèche ACE de spine (statique, voir Le spine (statique) d’une flèche) :
- 670 pour l’usage de cam "soft"
- 620 pour l’usage de cam "medium"
- 570 pour l’usage de cam "hard"
- 620 pour un arc classique.
Vous constatez alors que la flèche préconisée (en première intention) par le tableau pour un arc classique peut être plus raide que pour un arc à poulies utilisant des cam "soft". Le dilemme apparait si on se dit conjointement à ce résultat qu’"à allonge et puissance fixée, un arc à poulies est plus puissant qu’un arc classique" !
La solution
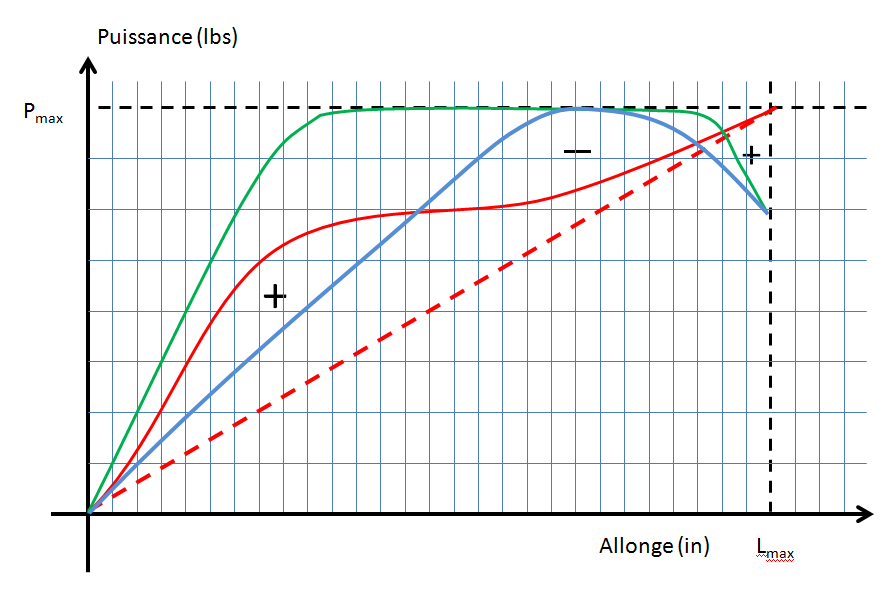
La solution de cet apparent paradoxe réside dans le fait que réduire un arc à la donnée de 2 paramètres (puissance, allonge) est trop réducteur, et l’on passe à coté de ce que contient la courbe "puissance versus allonge". Voici une série de courbe types :
- La courbe en pointillé rouge est représentation d’un arc droit dont la réponse est modèlisable par un ressort dont la tension (véritable sens de la "puissance d’un arc" ici) est proportionnelle à l’allongement ;
- la courbe rouge est celle d’un arc classique avec une inversion de courbure de branche ; elle démarre plus fort que celle du longbow pour finir à la même tension à pleine allonge ;
- la courbe verte est représentative d’un arc à poulie avec des cam "hard", le plateau est atteint assez vite et il est large (j’ai mis un let off assez élevé pour qu’il soit visible) ;
- la courbe bleu clair est représentative d’un arc à poulie muni de cam soft, le plateau est atteint tardivement et il est quasi inexistant (j’ai mis le même let off).
Bon, même si les courbes sont fictives elles vont montrer la voie de la solution. Ce qui compte en fait c’est la surface entre une courbe donnée et l’axe horizontal, c’est l’intégrale, qui donne l’énergie (en Joule, la vraie grandeur) emmagasinée lors de l’armement et qui va être restituée à la flèche lors de la décoche [1]. Plus cette énergie est grande (surface grande), plus la vitesse de libération est élevée (pour une même masse de flèche) mais aussi plus la déformation de la flèche peut-être élevée à souplesse égale (ou spine égal).
On conçoit alors aisément en comparant les surfaces en question qu’un arc à poulies "hard" par rapport à ’un arc à poulies "soft" emmagasine plus d’énergie, donc nécessite des flèches plus raides (spine plus petit), d’où le choix des spines 570 pour "hard cam" et 670 pour "soft cam".
Maintenant comparer l’énergie stockée de l’arc classique et celle de l’arc "soft", demande de comparer la somme des 2 aires notées "+" et de l’aire notée "-" entre les 2 courbes (rouge et bleu). Si la somme des aires "+" est plus grande que l’aire "-" alors l’arc classique stocke plus d’énergie, donc nécessite des flèches plus raides. D’où le choix du spine 620 pour l’arc classique plus raide que le 670 de l’arc à poulies "cam soft". CQFD !
Résumé
Donc, la moralité de cet intéressante question d’un étudiant en TIPE, est que réduire un arc à la donnée de sa puissance maximale donne des résultats paradoxaux. IL est clair que des logiciels bien étudiés prennent en compte au minimum la courbe "puissance vs allonge" afin d’associer une flèche ad equa.