Introduction
A la suite de l’annonce de nouvelles masselottes plus compactes, massives et modulables de la société Arc Système (voir page facebook d’AS) il y a eu pas mal de réactions positives sans doute justifiées.

Poids vs Inertie
Une chose sur laquelle je veux attirer l’attention par le biais de cet article concerne la comparaison inertiel de deux types de leste : l’un dont les masselottes sont réparties l’autre où elles sont concentrées. En effet, sur les photos suivantes ont peut voir à gauche une configuration avec des masselottes (sur le latéral) réparties sur une 20cm, alors qu’à droite les nouvelles masselottes sont concentrées sur 1 à 2 pouces.

|

|
Admettons que la masse $M$ de l’ensemble des masselottes soit la même dans les 2 configurations et que le centre de gravité des 2 systèmes soit à la même distance $R$ de la fixation à l’arc. On peut toujours s’arranger pour que l’équilibre de l’arc soit le même en jouant sur l’angle d’ouverture du latéral. Maintenant tous ces réglages se font en statique. Que se passe-t’il en dynamique ?
Avec le JO de Sochi 2014, on a eu l’occasion de voir des patineurs et patineuses sur glace par exemple et l’exemple typique de ce qui se passe dynamiquement est réalisé lors de pirouette où la personne après avoir lancé sa rotation se met à grouper ses bras le long du corps. Que se passe-t’il ? la vitesse de rotation augmente. C’est ce que l’on appelle la conservation du moment cinétique. Grossièrement la quantité :
$$ L = I \times \omega $$
est concernée avec $\omega$ la vitesse de rotation autour de l’axe de rotation considéré et $I$ le moment d’inertie de l’objet en question. Le moment d’inertie est défini pour un lot de masselottes de masse $m_i$ se mouvant en rotation par rapport à l’axe de rotation à une distance $r_i$
$$ I = \sum_i m_i r_i^2 $$
Dans le cas du patineur les bras se rapprochant du corps $r_i$ va diminuer, donc $I$ diminue, comme $L$ est constant, alors $\omega$ augmente, c’est-à-dire que le patineur tourne plus vite.
En fait la conservation du moment cinétique n’est pas toujours réalisée mais au moins cela nous a introduit le moment d’inertie d’un objet. Et là il a y a voir une différence de taille entre un masse $M$ répartie et une masse concentrée. Voyons les 2 cas de figure ci-dessous :
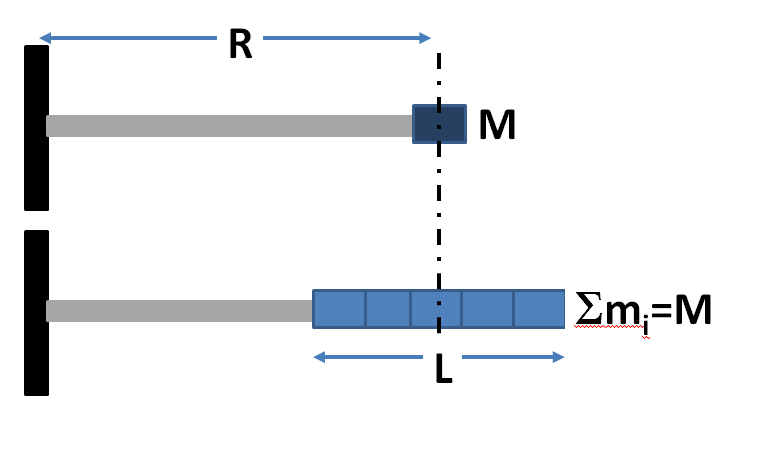
La configuration du haut (C1) représente un leste concentré, son moment d’inertie est donc approximativement égal à
$$ I_1 = M R^2 $$
La configuration du bas (C2) représente une collection de $N$ masselottes de masse individuelles $M/N$ réparties sur une longueur $L$ mais tout en gardant le milieu (lieu du centre de gravité) à une distance $R$ de l’axe comme pour C1. Le calcul directe du moment d’inertie s’écrit comme suit :
$$ I_2 = \sum_{i=0}^{N-1} m_i r_i^2 $$
avec $m_i = M/N$ (indépendant de l’indice "i") est $r_i = R-L/2+L i/(N-1)$
Le calcul de $r_i^2$ fait apparaitre 3 termes :
- le premier indépendant de "i" donne la contribution identique à $I_1$
$$ I_2^{(1)} = M R^2 = I_1 $$
- le second terme linéaire en "i" est nul ( c’est le résultat symétrie de la répartition des masses par rapport au centre de gravité)
- le troisième terme donne la contribution positive suivante
$$ I_2^{(3)} = \frac{ML^2}{12}\left[\frac{2(2N-1)}{N-1} - 3\right] $$
Contribution qui lorsque $N$ tends vers l’infini (barre homogène) devient égale au moment d’inertie d’une barre de longueur $L$ et de masse $M$.
Donc le moment d’inertie de la configuration C2 (répartie) est égal au moment d’inertie de la configuration C1 (concentrée) augmenté de la contribution du moment de l’ensemble des masselottes tournant autour d’un axe passant par le centre de gravité (c’est un résultat général dit du transport de du moment d’inertie) :
$$ I_2 = MR^2 + \frac{ML^2}{12}\left[\frac{2(2N-1)}{N-1} - 3\right] > I_1 $$
Imaginons que $L$ soit de l’ordre de grandeur de $R$ alors on voit que répartir les masselottes permet accroitre le moment d’inertie à masse égale et position du centre de gravité égale.
Épilogue
A quoi cela sert-il d’accroitre le moment d’inertie dans le cas d’un latéral pour un arc ? Et bien tout comme le patineur, pour que ce dernier freine sa rotation, il écarte ses bras pour augmenter son moment. L’arc est d’autant plus difficile à faire tourner que le moment d’inertie de son latéral est grand. Donc, si l’archer veut utiliser des masselottes concentrées, il va devoir soit augmenter $M$ (donc la masse totale) soit $R$ (donc écarter la masse de l’arc avec un latéral plus long). Dans le cas de l’usage de masselottes réparties l’ajustement se fait non seulement par l’intermédiaire de $M$ et $R$ mais aussi par le paramètre $L$ en jouant sur le terme $I_2^{(3)}$.
Donc, dire que concentrer les masselottes c’est le pieds, faut voir et en tous les cas cela enlève de la souplesse et à peut-être un effet sur la stabilité dynamique de l’arc par le biais du moment d’inertie. Donc des tests en perspective et merci à Arc Système de pouvoir nous donner de nouveaux joujoux.