Introduction
Nos flèches sont du point de vue de leur vitesse des avions en bout de piste de décollage : 250 à 300 km/h. On a vu aussi quelles sont soumises à une accélération de quelques 700g (cf. Dynamique (simple) d’une fléche en phase de propulsion) qui les fait plier et osciller sur elle-même (cf La paradoxe de l’archer). Après avoir passer la fenêtre d’arc, un vol plus ou moins balistique s’engage. Outre les effets de la pression de l’air, la flèche peut subir une force (couple de -) la faisant dévier de sa trajectoire idéale si elle a des défauts de symétrie. Et ce n’est pas un effet gyroscopique qui pourrait la maintenir dans le droit chemin comme je l’ai montré dans l’article Plumes collées en hélicoïdal (revisité).
Brisure de symétrie : induction d’un couple
La symétrie en question qui peut ne pas être respectée est celle qui concerne la révolution autour de l’axe longitudinal. Il peut y avoir plusieurs raisons à cette brisure de symétrie, par exemple : des plumes mal collées, un collage non uniforme de la pointe, un voilage des tubes alu (ou composite alu/carbone).
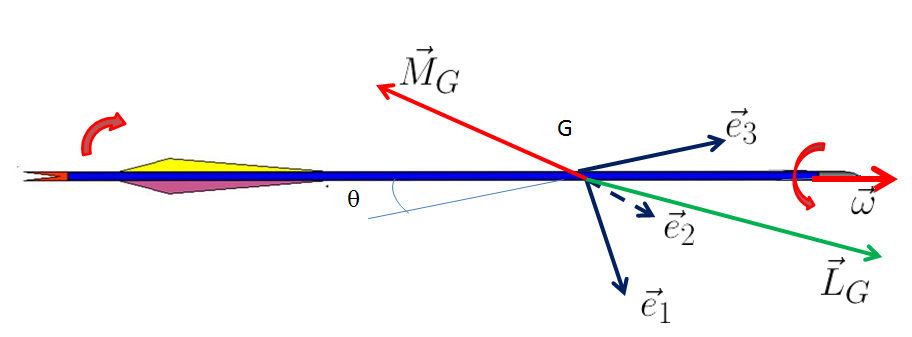
L’effet de la brisure de symétrie se traduit par des axes principaux d’inertie différents de l’axe longitudinal et les 2 axes perpendiculaires formant à eux trois un trièdre directe ($\vec{e}_1, \vec{e}_2, \vec{e}_3$).
Sur la figure ci-dessous, j’ai représenté ces axes principaux pris aux centre de gravité de la flèche en rotation autour de son axe longitudinal [1] (vecteur rotation $\vec{\omega}$).
Dans le repère des axes principaux, le vecteur de rotation $\vec{\omega}$ se décompose en
$$ \vec{\omega} = \omega \sin \theta\ \vec{e}_1 + \omega \cos \theta\ \vec{e}_3 $$
Dans le repère des axes principaux, par définition la matrice d’inertie est diagonale. Je ne vais considérer que des petites modifications par rapport au cas idéal, et donc elle a la forme de type
$$ \tilde{I}_G \approx \left( \begin{array}{ccc} I_x & 0 & 0 \\ 0 & I_y & 0 \\ 0 & 0 & I_z \end{array} \right) $$
avec dans notre cas $I_x \sim I_y \gg I_z$ à cause de la pointe qui contribue massivement à $I_x$ et $I_y$ (c’est plus difficile de faire tourner la flèche comme une majorette qu’en essayant de la faire pivoter comme une toupie).
Le moment cinétique de rotation de la flèche est donc le vecteur $\vec{L}_G$ d’expression :
$$ \vec{L}_G = \tilde{I}_G . \vec{\omega} = I_1 \omega \sin\theta\ \vec{e}_1 + I_3 \omega \cos\theta\ \vec{e}_3 $$
L’orientation de $\vec{L}_G$ dépend de $\theta$, c’est-à-dire du désalignement des axes principaux et aussi du rapport de grandeur entre $I_1$ et $I_3$.
La variation au cours du temps de ce moment cinétique est donné par l’expression de précession :
$$ \frac{d\vec{L}_G }{dt} = \vec{\omega} \wedge \vec{L}_G = (I_1 - I_3) \omega^2 \sin \theta \cos\theta \vec{e}_2 = \vec{M}_G $$
Le théorème du moment cinétique nous indique que l’expression de la variation du moment cinétique est relié au moment des forces qui vont agir sur la flèches. C’est un théorème en tout point identique (et même dérivé) du principe fondamental de la dynamique de Newton liant la variation de la quantité de mouvement à la présence de forces extérieures.
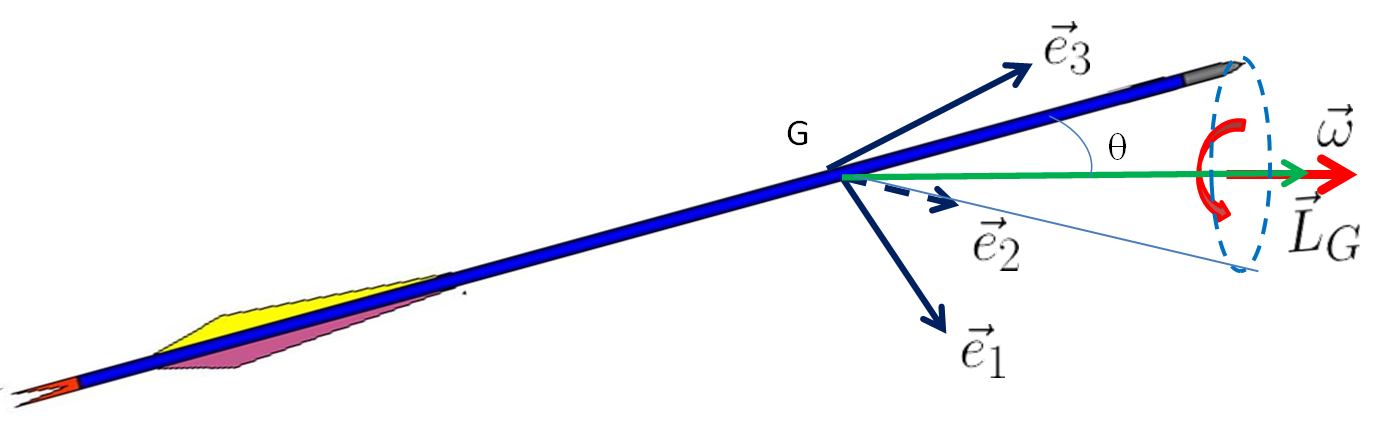
Le résultat est tout d’abord une précession du moment cinétique $\vec{L}_G$ autour du vecteur rotation \vec\omega, mais celle ci va se transformer en une variation de l’angle $\theta$ pour tendre à annuler le moment $\vec{M}_G$ alignant alors le vecteur rotation et $\vec{L}_G$. Car alors le produit vectoriel des deux vecteurs s’annule et la variation temporelle de $\vec{L}_G$ idem.
Au final, la flèche va donc être dans la configuration suivante
qui force la pointe à tourner et donc cela modifie le groupement en cible.
Conclusion
Donc un désalignement des axes principaux entraînant des efforts qui font dévier la flèche de sa trajectoire induisant une perte de groupement en cible. Il faut donc veiller au collage à 120° des plumes, à l’uniformité de collage de la pointe, à la rectitude des tubes alu et alu//carbone.