Introduction

Dans les articles Faites sonner les flèches ! (Partie I) et Faites sonner les flèches ! (Partie II) j’ai d écrit un dispositif expérimental permettant d’accéder aux vibrations libres d’une flèche à la suite d’une pichenette, c’est ce que l’on appelle la réponse impulsionnelle.

Le but de cet article est de modéliser les mouvements transverses d’une flèche et d’étudier leur spectre en fréquence.

Etablissement de l’équation de base des flexions

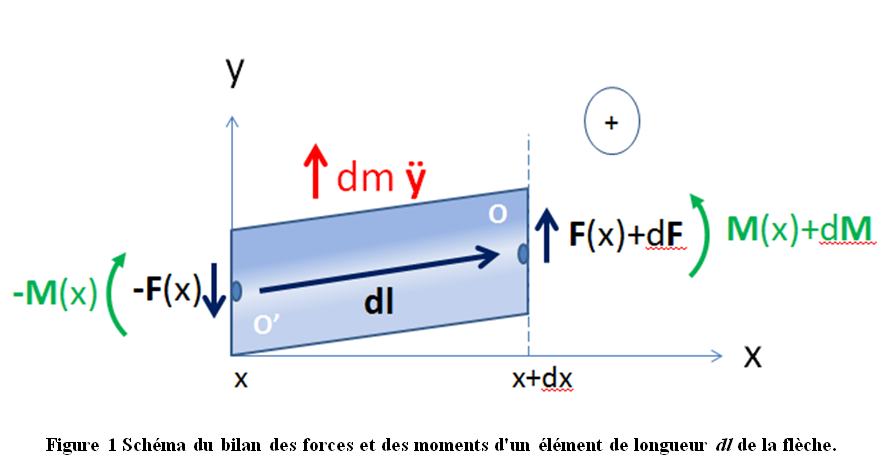
Sans refaire la théorie de l’élasticité [1], on peut qu’en même se faire un petit raisonnement des bilans des forces et moments agissant sur un petit tronçon de flèche (Figure 1). Il faut imaginer ce petit tronçon de longueur infinitésimale $d l $ connecté à ses voisins infiniment proches de lui sans dislocation.

Prenons le bilan des forces dans le cas où la flèche ne subit que des déplacements latéraux (ici notés selon l’axe $Y$). Sur les deux faces latérales (à gauche et à droite) s’exercent des forces dues aux contraintes internes : sur la face de droite (en $ x + dx $) $\vec{F}+d\vec{F}$ et sur la face de gauche (en $x$) $-\vec{F}$ [2]. Donc le bilan des forces de contraintes sur le tronçon est $d\vec{F}$, et cette résultante est responsable du mouvement latéral s’il n’y a pas de sollicitation extérieure par ailleurs. Si on note $dm$ la masse du tronçon et $\ddot{y}$ son accélération [3] alors le principe de la dynamique nous donne une première relation :

$$ d\vec{F} = dm \ddot{\vec{y}} $$

Si on divise par $dl$ la longueur du tronçon on fait apparaître la masse par unité de longueur $\mu$, ce qui donne

$$ \frac{d\vec{F}}{dl} = \mu \ddot{\vec{y}} \quad\quad (Eq.1) $$

Prenons maintenant les moments des forces de contraintes qui tendent à faire tourner une face sur elle-même. Le couple de ces forces de la face en $x+dx$ sur cette même face est notée $\vec{M}+d\vec{M}$ (et font tourner dans le sens « + »). Les contraintes appliquées sur la face en $x$ agissent aussi, premièrement par le biais du couple $-\vec{M}$ et le moment des forces $-\vec{F}$ appliquées en un point arbitraire O’ (voir figure) par rapport au point O qui vaut $(-\vec{dl})\times(-\vec{F})$ [4]. Comme le tronçon ne se met pas à pivoter sur lui-même en absence de contrainte extérieure spécifique (ex. couple de torsion transverse), nous obtenons la relation :

$$ -\vec{M} + (-\vec{dl})\times(-\vec{F}) + (\vec{M}+d\vec{M}) = 0 $$

Donc en simplifiant et en divisant par $dl$ :

$$ \frac{d\vec{M}}{dl} = \vec{F} \times \frac{\vec{dl}}{dl} $$

Or $\vec{dl}/dl$ est le vecteur unité tangente de la flèche (réduite à une simple ligne) que l’on note $\vec{t}$. Finalement, on obtient

$$ \frac{\vec{dM}}{dl} = \vec{F} \times \vec{t} \quad\quad (Eq.2) $$

Si à présent nous prenons l’Eq.2 et que nous la dérivons par rapport à l’élément de longueur, il vient :

$$ \frac{d^2\vec{M}}{dl^2} = \frac{d\vec{F}}{dl}\times \vec{t} + \vec{F}\frac{d\vec{t}}{dl} $$

Le second terme du membre de droite fait intervenir la dérivée de la tangente par rapport à $l$. Or pour des flexions de flèches petites par rapport à la longueur de la flèche (pas sa section !), ce terme peut être négligé car son module est égale à $1/R$ où $R$ est le rayon de courbure locale de la flèche. L’Eq.1 donne après calcul du produit vectoriel avec l’expression de la tangente $\vec{t}$ \propto (1, dy/dx), et le fait que pour des flexions petites $dl \ approx dx$ :

$$ \frac{d^2M}{dx^2} = - \mu \ddot{y} \quad\quad (Eq. 3) $$

L’expression du moment des contraintes $M(x,t)$ sort du cadre de cet article et l’on utilise le résultat suivant de mécanique des matériaux [5] :

$$ M(x,t) = E I \frac{\partial^2 y(x,t)}{\partial x^2} $$

avec $E$ le module d’Young caractéristique du matériau exprimé comme une pression en Pascal ($Pa$) et $I$ le moment d’inertie de la surface transverse de la flèche exprimée en $m^4$. Le produit $E I$ est appelé rigidité de la flèche et s’exprime en définitive en $N.m^2$. Nous avons déjà rencontré ce paramètre caractéristique dans l’article Le spine (statique) d’une flèche. En passant, nous avons fait l’hypothèse de caractéristiques ne variant pas le long de l’axe de la flèche (nous reviendrons sur ce point à la fin).

Ainsi, l’évolution de l’écart latéral $y(x,t)$ dans le cas de flexions petites et libres est gouvernée par l’équation différentielle suivante [6] :

$$ \mu \frac{\partial^2 y(x,t)}{\partial t^2} + E I \frac{\partial^4 y(x,t)}{\partial x^4} = 0 \quad\quad (Eq. 4) $$

Résolution : les modes propres

Afin de résoudre une telle équation, on pose $y(x,t) = Y(x)G(t)$ c’est-à-dire que l’on tente une séparation des variables espace et temps ($x$ et $t$). Les dérivées partielles n’agissant que sur l’une ou l’autre des deux fonctions auxiliaires, il vient :

$$ \mu Y(x) \ddot{G}(t) + E I G(t) Y^{\prime\prime\prime\prime}(x) = 0 $$

ou

$$ \frac{\mu}{EI} \frac{\ddot{G}(t)}{G(t)} = - \frac{ Y^{\prime\prime\prime\prime}(x)}{Y(x)} $$

On constate que de part et d’autre du signe $=$ il y a deux fonctions : l’une dépendant uniquement de $t$ tandis que l’autre ne dépendant que de $x$. Cette égalité étant vraie quelque soit $x$ (le long de la flèche) et quelque soit $t$ durant le laps de temps durant lequel l’équation reste valide. Ceci ne peut être réalisé que si et seulement si les deux fonctions sont égales à une et même constante que par commodité je note $-\beta^4$.
La variable $\beta$ est par ailleurs homogène à l’inverse d’une longueur (plus précisément l’unité est rad/m) et l’on la désigne sous le vocable de nombre d’onde.

On a donc deux équations liées l’une à l’autre :

$$ \begin{align*} Y^{\prime\prime\prime\prime}(x) - \beta^4 Y(x) &= 0 \quad\quad (Eq. 5a)\\ \ddot{G}(t) + \left ( \frac{E I}{\mu} \beta^4 \right ) G(t) &= 0 \quad\quad (Eq. 5b) \end{align*} $$

La seconde équation (Eq. 5b) est celle d’un oscillateur harmonique dont la pulsation $\omega$ (exprimée en rad/s) est égale à :

$$ \omega^2 = \frac{E I}{\mu} \beta^4 $$

Les solutions générales des Eq.5a,b sont donc pour des valeurs non nulles de $\omega$ (et $\beta$)
 [7]

$$ \begin{align*} G(t ;\omega) &= G_1 \sin \omega t + G_2 \cos \omega t \quad\quad (Eq. 6a)\\ Y(x ;\beta) &= Y_1 \sin \beta x + Y_2 \cos \beta x + Y_3 \sinh \beta x + Y_4 \cosh \beta x \quad\quad (Eq. 6b) \end{align*} $$

Dans le cas où $\omega = \beta = 0$, $Y(x)$ est un polynôme de degré 4 qui traduit des mouvements non-oscillants de translation, rotation… Ces cas ne nous intéressent pas dans cet article.

En règle générale, $\beta$ (et donc $\omega$) satisfait une équation ayant plusieurs solutions $\beta_0$, $\beta_1$, $\beta_2$, $\beta_3$... Et donc tout comme pour l’article Oscillations de la corde (Partie I) la solution générale $y(x,t)$ est une superposition de fonctions ou modes propres dont chacun s’écrit :

$$ y_n(x,t) = Y(x ; \beta_n) G(t ;\omega_n) \quad \mathrm{avec}\quad \omega_n = \frac{1}{L^2}\sqrt{\frac{E I}{\mu}} (\beta_n L)^2\quad\quad (Eq. 7) $$

J’ai introduit la longueur $L$ de la flèche pour rendre le facteur $\beta_n L$ sans dimension.

Conditions aux limites

Comme dans le cas de l’article Oscillations de la corde (Partie I), il faut adjoindre à l’Eq.7 des conditions aux limites comme les contraintes aux extrémités (par exemple) afin de procéder à la détermination des valeurs $\beta L$ (et $\omega$) qui définissent un mode propre de vibration de la flèche. La pertinence du choix des conditions aux limites peut être vérifiée en confrontant les résultats aux mesures.

Considérons que du coté de l’encoche (ou de la suspension dans nos tests) et de la pointe, la flèche est contrainte par le mouvement d’une masse concentrée $m_n$ ou $m_p$. Il faut reconnaître que c’est d’autant plus vrai pour la pointe of course même si celle-ci a une certaine longueur en général de plusieurs centimètres. Ainsi, on impose les conditions suivantes sur les moments et efforts internes :

$$ \begin{align*} M(0,t) &= 0 \\ -F(0,t) &= m_n \ddot{y}(0,t)\\ M(L,t) &= 0 \\ F(L,t) &= m_p \ddot{y}(L,t) \end{align*} $$

Nb : pour obtenir les contraintes il faut se représenté le petit bout de tube Figure 1 auquel on adjoint une masse soit à sa gauche dans le cas $x=0$ ou bien à sa droite dans le cas $x=L$. D’où le changement de signe pour les efforts aux deux extrémités.

Ces 4 contraintes se traduisent par des conditions sur la fonction $Y(x)$ (attention la dérivée seconde des fonctions sinus et cosinus introduit un signe « - ») :

$$ \begin{align*} Y(0) &= 0 \\ Y^{\prime\prime\prime}(0) &= \frac{ m_n}{\mu L^4} (\beta L)^4 Y(0) \quad\quad (Eq. 8a) \\ Y^{\prime\prime}(L) &= 0 \\ Y^{\prime\prime\prime}(L) &= -\frac{m_p}{\mu L^4} (\beta L)^4 Y(L) \quad\quad (Eq. 8b) \end{align*} $$

Nous avons affaire en fait à un système de 4 équations à 4 inconnues ${Y_i, i=1,\dots,4}$ homogène ($\beta L$ est remplacé par $x$ par commodité d’écriture) :

$$ \left( \begin{array}{cccc} 0 & -1 & 0 & 1 \\ -\sin x & -\cos x & \sinh x & \cosh x \\ 1 & \frac{m_n }{\mu L}x & -1 & \frac{m_n }{\mu L}x \\ \frac{m_p }{\mu L}x \sin x & \frac{m_p}{\mu L}x \cos x & \frac{m_p}{\mu L}x \sinh x & \frac{m_p }{\mu L} x \cosh x \\ -* \cos x & + \sin x & +\cosh x & + \sinh x \end{array} \right) \left( \begin{array}{cccc} Y_1 \\ Y_2 \\ Y_3 \\Y_4 \\ \ \end{array}\right ) =0 \quad\quad (Eq.9) $$

Ce système ressemble à celui rencontré lors de la discussion dans l’article Oscillations de la corde avec masselotte centrale (Partie II). Pour qu’il y ait une solution non triviale pour laquelle tous les $Y_i = 0$, il faut que le déterminant du système (Eq.9) soit nul. Cela fournit une équation à laquelle doit satisfaire $\beta L$, à savoir :

$$ \begin{align*} (\mu L)^2(\cos x \cosh x -1 ) &+ \mu L (m_p + m_n) x (\cos x \sinh x - \sin x \cosh x) \\ &-\ 2 m_p m_n x^2 \sin x \sinh x = 0 \quad (Eq.10) \end{align*} $$

Cas particuliers théoriques

De l’Eq.10 on peut tirer des cas particuliers selon les valeurs de $m_n$ (masse de l’encoche) et $m_p$ (masse de la pointe), lesquels sont soient des cas de mécanique standard dans le domaine des poutres/barres en flexion soient des cas de configuration flèche-encoche-pointe « de laboratoire ».

• Si $m_n = m_p = 0$, on a uniquement le tube, alors les conditions Eq.8a.b sont celles d’oscillations « libres » aux deux bouts. L’Eq.10 se réduit alors à :

$$ \cos x \cosh x = 1 \quad\quad (Eq.10a) $$

Les valeurs de $\beta L$ satisfaisant cette équation sont donc égales à :

$$ \beta_i L \approx \left \{0, 4.73004, 7.85320, \dots, (2 i +1)\frac{\pi}{2} \right \} $$

La valeur 0 signifie juste qu’il y a un mouvement non-oscillant (translation verticale) possible mais cela il ne nous intéresse pas ici.

• Si $m_n, m_p \rightarrow \infty$, les conditions Eq.8a.b sont celles d’appuis « simple » à chaque extrémité, alors on a
  

  $$ x \sin x \sinh x = 0 \quad\quad (Eq.10b) $$

  
  qui donne les valeurs
  

  $$ \beta_i L = i \pi\quad I = 0, 1,\dots $$

  
  Ce cas est bien étudié dans le cas des poutres mais ne nous servira pas dans notre étude.

• Si $m_p = 0$ (pas de pointe) alors les valeurs de $x$ satisfont l’équation (condition d’oscillations libres de ce coté) :

$$ \frac{m_n}{\mu L} = \frac{1 - \cos x \cosh x}{x (\cos x \sinh x - \sin x \cosh x)} \quad\quad (Eq.10c) $$

Un exemple de résolution graphique est donné en Figure 2 dans le cas où $m_n \approx 5\% (\mu L)$ (typiquement une encoche de 7 grains pour un tube de 140 grains). Les valeurs de $\beta L$ sont comprises en fait entre les valeurs qui annulent le numérateur et celles qui annulent le dénominateur. Notons que si $m_n$ croit les fréquences ont tendance à diminuer (décalage vers de plus petites valeurs).

• Un cas similaire au précédent avec cette fois l’encoche considérée comme de masse négligeable $m_n \ approx 0$. On obtient alors l’équation

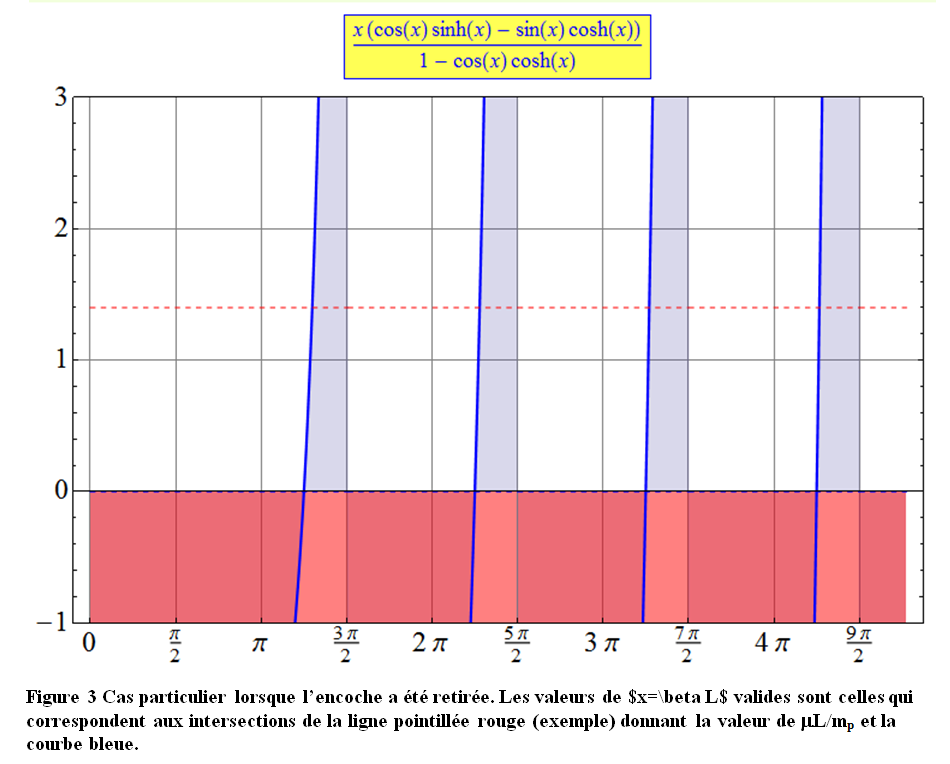
$$ \frac{\mu L}{m_p} = \frac{x (\cos x \sinh x - \sin x \cosh x)}{1 - \cos x \cosh x} \quad\quad (Eq.10d) $$

Notez que cette façon de présenter permet de restreindre entre 1/2 et 2 les valeurs pratiques du rapport $\mu L/m_p$. Un exemple de résolution graphique est donné sur la Figure 3 dans le cas où $\mu L = 1.4 m_p$ (typiquement une pointe de 100 grains et un tube de 140 grains). Notons là aussi que plus la pointe s’alourdie plus les fréquences se décalent vers de plus petites valeurs.

Pour donner une idée des valeurs de $\beta L$ dans les différents cas de figure précédents j’ai pris $m_n = 7$gr, $m_p = 100$gr et $\mu L = 140$gr. La Table 1 donne les 4 premières fréquences (hors-mis la fréquence 0 même si elle fait partie du spectre).

Pour obtenir le spectre en fréquence on a besoin de la rigidité du tube ($\omega = 2\pi \nu$)

$$ \nu_k = \frac{1}{2\pi}\sqrt{\frac{E I}{\mu L^4}} (\beta_k L)^2 \quad\quad (Eq.11) $$

Imaginons une ACE 670 dans les conditions de la Table 1, on obtient alors les fréquences suivantes de la Table 2.

Enfin, les modes propres ont la forme générale suivante à une constante de normalisation près (cas de masse aux deux bouts) :

$$ \begin{array}{rcl} Y_k(x) &= &\sin \beta_k x \\ & +& \frac{\mu L (\sin \beta_k L-\sinh \beta_k L)}{ 2 m_n \beta_k L \sinh \beta_k L + \mu L ( \cosh \beta_k L - \cos \beta_k L)} (\cos \beta_k x + \cosh \beta_k x) \\ & + & \frac{2 m_n \beta_k L \sin \beta_k L + \mu L ( \cosh \beta_k L - \cos \beta_k L) }{ 2 m_n \beta_k L \sinh \beta_k L + \mu L ( \cosh \beta_k L - \cos \beta_k L)} \sinh \beta_k x \end{array} $$

Cas atypiques expérimentaux

Avant d’envisager d’étudier les résultats obtenus pour l’article Faites sonner les flèches ! (Partie II), j’ai procédé à des mesures sur des cas « atypiques ».

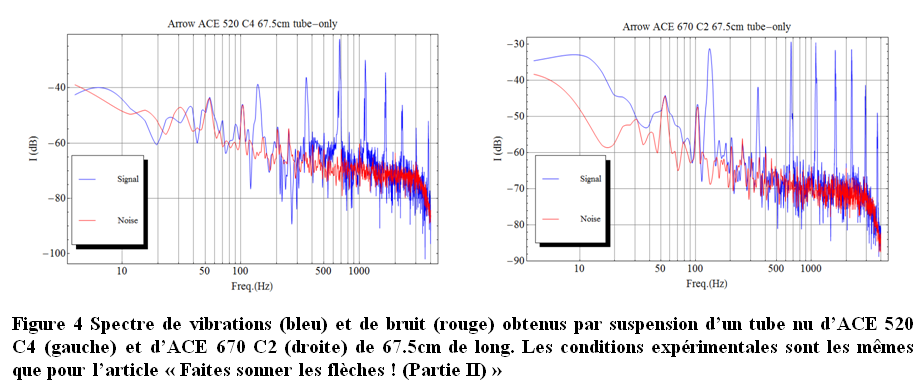
Prenons par exemple les spectres de vibrations et bruits de tubes nus : une ACE 520 C4 (6.65gr/in) et une ACE 670 C2 (5.64gr/in) de 67.5cm de long (26.6in). Notez que les masses par unité de longueur mesurées et utilsées ici sont légèrement différentes de celles que l’on trouve soit dans le Shaft Selector d’EASTON ou bien OnTarget. Ceci vient des différentes « moutures » d’ACE selon le chiffre après a lettre « C ». Ceci dit, on obtient pour chaque flèche dans l’intervalle de fréquences analysées, 8 pics qui se détachent bien du fond (Figure 4).

La Table 3 donne les valeurs des pics de fréquences mesurées (erreur de l’ordre de 3MHz) et celles calculées à l’aide des équations Eq.10a et 11.

Les valeurs calculées sont en accord raisonnable (à 5% près) et qualitativement le changement de rigidité de la flèche est bien reproduit. On voit bien que c’est un effet qui évolue lentement car en racine carrée donc pour avoir un effet de doublement de fréquence il faudrait multiplier par 4 la rigidité !

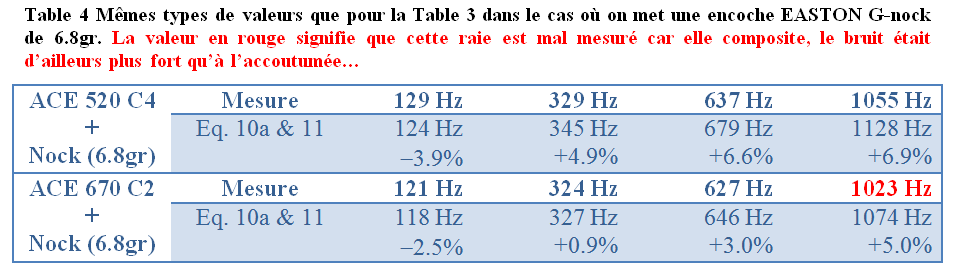
Si on ajoute à présent des encoches EASTON G-nocks de 6.8gr aux 2 tubes précédents, on obtient des résultats reportés dans Table 4.

Les valeurs mesurées et calculées sont toujours raisonnablement en accord. On note aussi qu’ajouter une encoche diminue les fréquences propres (passage de la Table 3 à la Table 4) et que l’ampleur de la diminution est bien reproduite par les valeurs calculées soit environ (10Hz, 25Hz, 40Hz, 60Hz) pour les 4 premières fréquences.

Résumé et perspectives

Dans cet article j’ai développé un modèle des vibrations libres de la flèche en faisant appel aux résultats de théorie de l’élasticité appliquée aux vibrations de poutres. Dans ce type de problèmes que nous avons déjà abordés pour le cas de la corde, il y a la partie « équation générale » décrivant les mouvements transverses du tube lui-même, mais aussi les conditions de mouvements aux deux extrémités.

J’ai étudié le cas général, bien que simplifié, de conditions liées à la présence de masses localisées aux deux extrémités modélisant l’encoche et la pointe. En passant les cas limites où il n’y a pas d’encoche, de pointe ou bien au contraire où elles sont tous les deux de masses « infinies » ont été discutés.

J’ai négligé la suspension. Ceci dit j’aurai pu introduire formellement une force de type « ressort » dont la raideur (force par unité de longueur d’élongation) aurait été donnée par une expression de type $k \approx m_T g/l_{susp}$ avec $m_T$ la masse totale en suspension, $g$ l’accélération de la pesanteur et $l_{susp}$ la longueur de la cordelette de suspension. Or, quand on introduit cette condition supplémentaire on s’aperçoit que le « poids » respectif de cette nouvelle contrainte par rapport à celle déjà introduite par le biais de la masse de l’encoche est donné par le rapport :

$$ \frac{k L^3}{EI} \frac{\mu L}{m_n} \frac{1}{(\beta L)^4} \approx 4\times 10^{-4}\ll 1 $$

Etant très inférieur à 1 en pratique, je pense que le léger désaccord calcul/mesure ne semble pas lié à la condition de suspension.

Il y a peut-être quelque chose à creuser par contre du coté de l’invariance de la rigidité le long de la flèche car on sait et on peut le constater avec un pied à coulisse, que le diamètre extérieur des ACE n’est pas constant : plus grand coté pointe, plus fin coté encoche. Donc à la fois le moment d’inertie $I$ et la masse par unité de longueur $\mu$ dépendent de $x$. Le hic c’est que l’Eq. 4 devient alors :

$$ \mu(x) \frac{\partial^2 y(x,t)}{\partial t^2} + E \frac{\partial^2}{\partial x^2}\left ( I(x) \frac{\partial^2 y(x,t)}{\partial x^2} \right ) = 0 $$

Or cette équation n’est plus à variables séparables !!! Donc il faut utiliser d’autres techniques…

J’ai dans l’idée d’utiliser des tubes non profilés pour tester en pratique l’influence des la section variable des ACEs sur le spectre de fréquences.

A suivre !