Introduction
Cet article fait suite à Oscillations de la corde (Partie I) où j’ai établi l’équation d’ondes à 1 dimension qui régit l’évolution du déplacement transversal d’un
élément de corde $u(x,t)$ :
$$ \mu(x) \frac{\partial^2 u(x,t)}{\partial t^2} = T_0 \frac{\partial^2 u(x)}{\partial x^2} \quad\quad (Eq. 1) $$
Avec $T_0$ la tension constante de la corde, et $\mu(x)$ la masse par unité de longueur qui peut dépendre de la position $x$ comprise entre 0 et $L$ la longueur de la corde.
J’avais adjoint à l’Eq.1 une série de contraintes globales (Cg.1) que je rappelle pour mémoire :
- les points de fixation de la corde aux deux bouts : $u(0,t) = u(L,t) = 0$ pour toute valeur de $t \geq 0$ ;
- la forme de la corde à l’instant 0 : $u(x,0) = f(x)$ ;
- et la vitesse de la corde à l’instant 0 : $v(x,0) = \frac{\partial u}{\partial t} (x,0) = g(x)$. Si on lâche la corde alors $g(x)=0$.
Après avoir étudié les fonctions spéciales appelées « modes » , j’ai pu résoudre le problème de l’évolution d’une corde de masse linéique constante, lâchée sans vitesse d’une position initiale ressemblant à la forme de la corde à pleine allonge (triangulaire). Le résultat est que la corde se déplace à vitesse constante, dans un mouvement alternatif entre sa position initiale et la position symétrique par rapport à l’axe des abscisses (position au repos de la corde).
Numériquement, j’avais également mis en évidence une vitesse d’évolution un peu trop rapide bien que dans le bon ordre de grandeur (cf. quelques millisecondes) par rapport au résultat établi lors de l’étude de la phase de propulsion d’une flèche. Et bien justement, quelle est donc l’influence de la flèche ? C’est la raison de cet article mais avant je vais revenir sur l’Eq.1 et sa résolution quand on ajoute des masses ponctuellement sur la corde que l’on considère toujours de masse linéique constante.
Corde et masses ponctuelles
Dans l’Eq.1, j’ai fait figurer une masse linéique $\mu(x)$ dépendant de la position $x$ le long de la corde. Justement rajouter des masses ponctuelles $m_i$ aux positions $x_i$ ($i =1,\ 2,\ \dots,\ N$) peut se faire de la façon suivante :
$$ \mu(x) = \mu_0 + \sum_{i=1}^{N} m_i \delta(x-x_i) $$
avec $\delta(x-x_i)$ une « fonction » très piquée en $x=x_i$ appelée delta de Dirac en l’honneur du physicien d’origine suisse Paul Adrien Maurice Dirac Prix Nobel 1933 pour la mise œuvre d’une facette de la théorie quantique de l’atome et ayant introduit la notion d’anti-matière… Mais ceci est une autre histoire. [1]. (nb. la fonction $\delta(x)$ a une dimension de l’inverse d’une longueur donc pas d’inquiétude l’expression est bien homogène).
Aux contraintes globales (Cg.1) rappelées dans l’introduction viennent s’ajouter deux types de contraintes (Cg.2) au niveau des positions $x_i$ :
$$ \begin{align*} u(x_i^{+}) &= u(x_i^{-}) \\ T_0 \left[ \frac{\partial u}{\partial x}( x_i^{+},t) - \frac{\partial u}{\partial x}( x_i^{-},t) \right] &= m_i \frac{\partial ^2 u}{\partial t^2}( x_i,t) \end{align*} $$
La notation $x_i^{-}$ ($x_i^{+}$) signifie une position légèrement inférieure (supérieure) à $x_i$. La première contrainte n’est autre que l’expression de la continuité de la corde (c’est la moindre des choses) et la seconde est issue de l’Eq.1 intégrée autour de la position $x_i$ et la propriété de la fonction delta, c’est-à-dire :
$$ \int_{x_i-h}^{x_i+h}\delta(x-x_i) f(x)dx = f(x_i) $$
Donc les nouvelles contraintes sont tout compte fait assez logiques, non ? Ceci dit la seconde contrainte signifie qu’il y a une discontinuité de la pente à chaque position où il y a une masselotte.
Pour résoudre l’Eq.1 affectée des deux types de contraintes Cg.1 et Cg.2, on introduit comme lors de l’article I, les fonctions « modes » définies par :
$$ \Phi(x,t) = \Phi(x) \cos(\omega t + \phi) $$
Ces fonctions doivent satisfaire les relations suivantes (Eq. 2) :
$$ \begin{align*} T_0 \frac{\partial^2 \Phi}{\partial x^2}( x,t) + \mu_0 \omega^2 \Phi(x,t) &= 0 \\ \Phi(0) = \Phi(L) &= 0\\ \Phi(x_i^{+}) &= \Phi(x_i^{-}) \\ T_0 \left[ \frac{\partial \Phi}{\partial x}( x_i^{+}) - \frac{\partial \Phi}{\partial x}( x_i^{-}) \right] &= -m_i \omega^2 \Phi( x_i) \end{align*} $$
Une masselotte au centre de la corde
En introduction, j’ai fait allusion à la flèche, car en effet lors de la phase de propulsion celle-ci est attachée à la corde donc il parait naturelle de tenir compte sa masse ! On la note $M$, et par simplicité elle est placée au milieu soit à $x=L/2$. Pour les applications numériques je prends $M \approx 20\mathrm{g} \approx 2 m_c$ (j’ai pris une flèche ACE 620 de 67.5cm chargée à 120 grains). Donc, localement on concentre une masse double de la corde elle-même…
Si on inspecte la série de relations Eq.2, on se rend compte que la fonction $\Phi(x)$ satisfait une équation identique à celle rencontrée lors de la résolution du problème avec masse linéique constante. Ce qui change c’est qu’il faut considérer les morceaux de corde de par et d’autre de la masse centrale indépendants l’un de l’autre dans un premier temps. Donc, on peut paramétrer la fonction $\Phi(x)$ comme suit :
$$ \Phi(x) = \left\{\begin{matrix} A_{-} \sin k x + B_{-} \cos k x & \quad\quad & 0\leq x \leq L/2 \\ A_{+} \sin k (x-L) + B_{+} \cos k (x-L) & \quad\quad & L/2 \leq x \leq L \end{matrix}\right. $$
Les contraintes aux deux bouts de corde annulent les valeurs de $B_-$ et $B_+$, donc
$$ \Phi(x) = \left\{\begin{matrix} A_{-} \sin k x & \quad\quad 0\leq x \leq L/2 \\ A_{+} \sin k (x-L) & \quad\quad L/2 \leq x \leq L \end{matrix}\right. $$
La première équation du système Eq.2 permet de retrouver la relation de dispersion que nous avons déjà rencontrée à savoir :
$$ \omega = c k \quad\quad \mathrm{avec} \quad\quad c =\sqrt{\frac{T_0}{\mu_0}} $$
Les relations de continuité de la corde et de discontinuité de la pente au milieu de la corde donnent un système linéaire homogène à 2 équations aux 2 variables $A_-$ et $A_+$ (Syst. 1) :
$$ \left\{\begin{matrix} A_- \sin \frac{k L}{2} + A_+ \sin \frac{k L}{2} &=& 0 \\ A_- \left(p \sin \frac{k L}{2} - 2 \cos \frac{k L}{2}\right) + A_+ \left(-p \sin \frac{k L}{2} + 2 \cos \frac{k L}{2}\right) & = & 0 \end{matrix}\right. $$
J’ai mis le système sous cette forme car nous la généraliserons quand on rajoutera des masselottes. De plus j’ai mis à profit de la continuité de la corde pour calculer $\Phi(L/2)$. Enfin, pour alléger la notation le paramètre $p$ est égal à :
$$ p = \frac{M \omega^2}{k T_0} = \frac{M}{m_c} k L $$
Un système linéaire homogène du type générique suivant où $\mathbf{D}$ est une matrice carrée :
$$ \mathbf{D}.x = 0 $$
possède une solution triviale $x=0$ sauf si la matrice n’est pas inversible.
Dans notre cas, cela signifie qu’éviter la solution triviale $A_- = A_+ = 0$ qui donnerait une corde immobile dans sa position au repos (on a déjà vu ce raisonnement…), donne la contrainte de nullité du déterminant de la matrice
$$ \begin{vmatrix} \sin \frac{k L}{2} & \sin \frac{k L}{2} \\ p \sin \frac{k L}{2} – 2 \cos \frac{k L}{2} & -p \sin \frac{k L}{2} + 2 \cos \frac{k L}{2} \end{vmatrix} = 0 $$
Ce qui se traduit par l’équation que satisfait $k$ (Eq.3) :
$$ \sin \frac{k L}{2} \left( -p \sin \frac{k L}{2} + 2 \cos \frac{k L}{2} \right) = 0 $$
L’équation Eq.3 est satisfaite si l’un ou l’autre des termes est nul. Cela donne 2 séries distinctes a priori de solutions.
Modes et fonctions propres de la première série
La première série
$$ \sin \frac{k L}{2} = 0 \quad\quad \Rightarrow k_n = n \frac{2\pi}{L}\quad\quad n=1,\ 2,\ \dots $$
présente des valeurs de $k$ quantifiées (cf. valeurs indicées par un nombre entier) multiples de $k_1 = 2\pi/L$. Ce type de quantification a été rencontrée déjà lors de la résolution du problème sans masse ajoutée (notée cependant la différence $L \rightarrow L/2$).
Dans cette série de valeurs, on en conclue que pour toutes les valeurs de $n$ le système Syst.1 implique que
$$ A_{-,n} = A_{+,n} \equiv A_n $$
Donc, les fonctions propres s’écrivent
$$ \Phi_n(x) = \left\{\begin{matrix} A_n \sin k_n x & \quad\quad 0\leq x \leq L/2 \\ A_n \sin k_n (x-L) & \quad\quad L/2 \leq x \leq L \end{matrix}\right. $$
Or, étant donné l’expression de $k_n$ on se rend compte que l’on peut simplifier l’écriture et donc on obtient
$$ \Phi_n(x) = A_n \sin k_n x = A_n \sin 2\pi n \frac{x}{L} $$
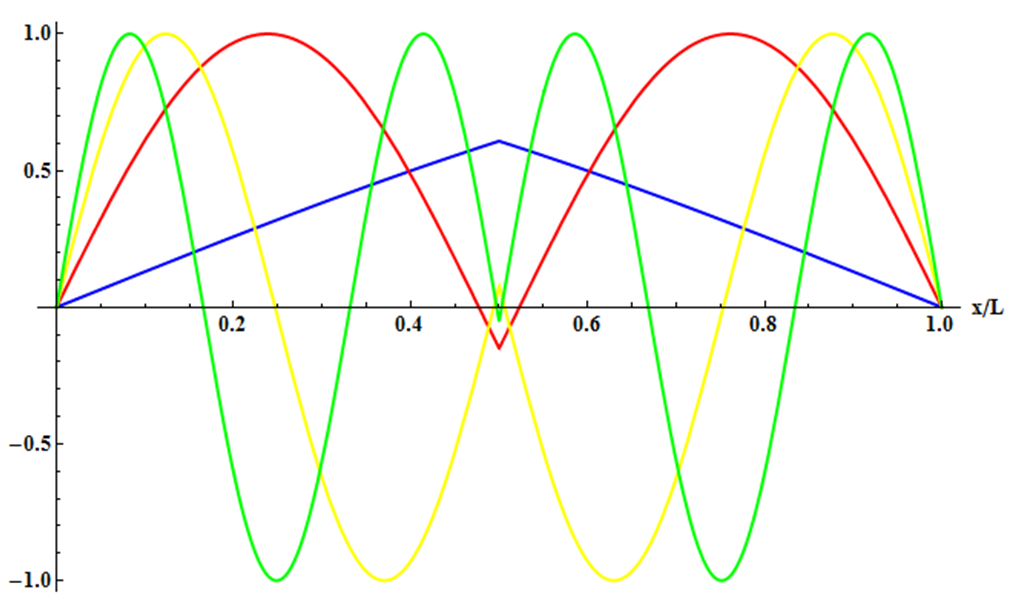
Ces fonctions sont les modes impairs anti-symétriques par rapport à $x=L/2$, c’est-à-dire $\Phi_n(L/2-h) = - \Phi_n(L/2+h)$ (pour $-L/2 \leq l \leq L/2$). La figure 1 donne les deux premières fonctions pour fixer les idées.
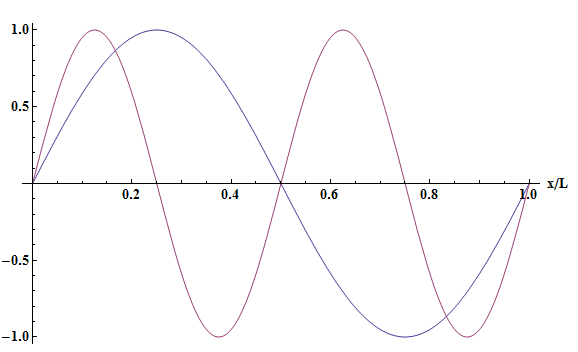
Figure 1 Les 2 modes propres de la première série de valeurs de k solution de l’Eq.3
Si on se souvient de la discussion de la décomposition de la fonction $f(x)$ (forme initiale de la corde) sur les fonctions modes propres dans le cas sans masselotte, on peut intuiter que ces fonctions impaires ne seront pas exciter si $f(x)$ est symétrique par rapport à $x=L/2$.
D’autre part ces solutions de la premières séries sont continues en $x=L/2$.
Modes et fonctions propres de la seconde série
Abordons le cas de la seconde série de fonctions propres découlant de l’Eq. 3 pour lesquelles cette fois j’ai inclus la définition du paramètre $p$ en fonction de $k$ :
$$ -* \frac{M}{m_c}kL \sin \frac{k L}{2} + 2 \cos \frac{k L}{2} = 0 \quad\quad (Eq. 4) $$
Les solutions de cette équation peuvent être visualisées graphiquement (Fig. 2) pour différentes valeurs du rapport $M/m_c$.
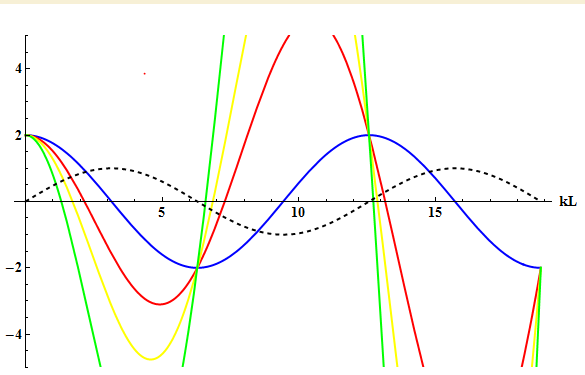
Figure 2 Fonctions permettant de trouver les solutions de l’Eq.4. Les courbes de couleur bleue, rouge, jaune et verte déterminées pour les rapports M/mc = 0, 1/2 , 1 et 2. Les valeurs annulant la courbe noire sont données par la première série de valeurs de l’Eq. 3.
Ce que l’on peut remarquer tout d’abord c’est que si $M/m_c = 0$, l’Eq. 4 se simplifie en
$$ \cos \frac{k L}{2} = 0 \quad\quad\Rightarrow k_m = (2m+1)\frac{\pi}{L}\quad\quad m=0,\ 1,\ \dots $$
Dans ces conditions les valeurs de $k$ solutions de la première et seconde série sont complémentaires et l’on retrouve en fait toutes les valeurs multiples de $\pi/L$ comme nous l’avions établi dans l’article Oscillations de la corde (Partie I).
Pour une valeur de $M$ non nulle, on constate :
- plus $M$ est grand, plus la première valeur solution est faible tendant vers 0 à l’infini et, c’est la première des solutions même en prenant en compte la première série de solutions de l’Eq.3 ;
- les solutions suivantes se confondent de plus en plus avec les solutions de $\sin k L/2 =0$ tout en étant légèrement plus grandes.
La seconde remarque permet en fait d’intercaler les solutions des 2 séries de l’Eq. 3. Voici les valeurs solutions $k_n L$ dans le cas où $M=2 m_c$ :
| n | Série 1 | Série 2 |
| $1$ | $1.3065$ | |
| $2$ | $2\pi$ | |
| $3$ | $ 6.5846$ | |
| $4$ | $4\pi$ | |
| $5$ | $ 12.7232$ | |
| $6$ | $6\pi$ | |
| $7$ | $18.9550$ | |
| $8$ | $8\pi$ |
Alors que sont les fonctions propres correspondantes aux valeurs de $k$ de la seconde série ?
En revenant au système Syst.1, pour cette série de valeurs de $k$, on obtient la contrainte :
$$ A_{-,2p+1} = - A_{+,2p+1} \equiv A_{2p+1}\quad\quad p=0,\ 1,\ \dots $$
Pour l’étiquetage j’ai tenu compte des remarques précédentes. Donc, les fonctions propres s’écrivent
$$ \Phi_{2p+1}(x) = \left\{\begin{matrix} A_{2p+1} \sin k_{2p+1} x & \quad\quad 0\leq x \leq L/2 \\ -* A_{2p+1} \sin k_{2p+1} (x-L) & \quad\quad L/2 \leq x \leq L \end{matrix}\right. $$
Ces fonctions contrairement à celles de la première série sont symétriques par rapport à $x=L/2$ et de pente discontinue en ce point. Remarquez que ces 2 caractéristiques sont très intéressantes dans notre étude… Sur la figure 3 sont présentées les premières fonctions de cette série pour fixer les idées. Remarquez également les « sursauts » autour de l’axe des abscisses en $x=L/2$ pour les fonctions au-delà de la première.
Figure 3 Les 4 premières fonctions propres de la seconde série : bleu (n=2), rouge (n=4), jaune (n=6) et verte (n=8). On note bien la discontinuité de pente en x = L/2 et leur symétrie par rapport à cette position.
Solution dans le cas d’une corde à pleine allonge
La solution générale de l’Eq.2 dans le cas d’une masselotte au centre de la corde peut donc s’écrire selon le principe de linéarité comme
$$ u(x,t) = \sum_{n=1}^{\infty} A_n \Phi_n(x) \cos(c k_n t + \phi_n) $$
(rappel : l’indice $n$ pointe alternativement sur une fonction propre de la seconde et de la première série)
Il faut prendre en compte 2 contraintes encore à savoir la forme et vitesse initiale de la corde. Si nous lâchons la corde sans vitesse, on peut se convaincre que $\phi_n = 0$ pour toute valeur de $n$ (voir l’article Oscillations de la corde (Partie I)). Du coté de la forme initiale $f(x)$, il est en fait possible de projeter cette fonction sur la base des fonctions propres $\Phi_n(x)$ comme on a pu le faire avec les fonctions $\sin$ comme les série de Fourier. Donc, si
$$ f(x) = \sum_{n=1}^{\infty} A_n \Phi_n(x) $$
Le calcul des coefficients $A_n$ se fait par la relation suivante :
$$ A_n = \frac{\int_0^L f(x) \Phi_n(x) \mu_0 dx + M f(L/2) \Phi_n(L/2)}{ \int_0^L \Phi_n(x) \Phi_n(x) \mu_0 dx + M \Phi_n^2(L/2)} $$
(la démonstration dépasse largement le cadre de cet article).
Si l’on prend la fonction $f(x)$ en forme de triangle que nous avons déjà rencontré lors de l’article précédent :
$$ f(x) = \left\{ \begin{array}{rl} 2\frac{H}{L}x & \mathrm{si}\quad 0 \leq x\leq L/2 \\ 2\frac{H}{L} (L-x) & \mathrm{si}\quad L/2 \leq x\leq L \end{array} \right. $$
Cette fonction ayant la propriété d’être symétrique et de pente discontinue en $x=L/2$ impose la nullité des coefficients $A_{2p} = 0$ (la vérification est laissée au lecteur !). Pour le calcul de $A_{2p+1}$, prenons tout d’abord le calcul de l’intégrale du numérateur. La symétrie par rapport à $x=L/2$ fournit la relation (notez que $\mu_0$ constante peut sortir de l’intégrale)
$$ \begin{align*} N_1 &= \mu_0 \int_0^L f(x) \Phi_{2p+1}(x) dx = 2\mu_0 \int_0^{L/2} f(x) \Phi_{2p+1}(x) dx \\ &= \frac{4 \mu_0 H}{L} \int_0^{L/2} x \sin k_{2p+1} x dx \\ &= \frac{4 \mu_0 H}{k_{2p+1}L} \left[ -* \frac{ k_{2p+1}L }{2} \cos \frac{ k_{2p+1}L }{2} + \sin\frac{ k_{2p+1}L }{2} \right] \end{align*} $$
Or, il faut se souvenir que nous avons à faire à des valeurs de $k_{2p+1}$ de la seconde série et donc
$$ \cos \frac{ k_{2p+1}L }{2} = \frac{p}{2} \sin \frac{ k_{2p+1}L }{2} $$
Donc, en reportant cette relation et redonnant la valeur de $p$ en fonction des masses et de $k_{2p+1} L$, il vient que le terme intégral est donné par
$$ N_1 = \frac{4\mu_0 H}{k_{2p+1}^2 L} \left( 1- \frac{M}{m_c} \frac{( k_{2p+1}L)^2}{4} \right) \sin \frac{k_{2p+1}L }{2} $$
Le deuxième terme du numérateur ne pose pas de problème, il s’écrit
$$ N_2 = M H \sin \frac{k_{2p+1}L }{2} $$
Pour ce qui concerne le dénominateur, en exploitant la symétrie de $\Phi_{2p+1}(x)$ , il vient
$$ D = \frac{m_c}{2}\left( 1 + \frac{M}{m_c}\sin^2\frac{k_{2p+1}L }{2} \right) $$
En rassemblant les termes $N_1$, $N_2$ et $D$, on obtient l’expression des coefficients $A_{2p+1}$ suivante :
$$ A_{2p+1} = \frac{8 H}{(k_{2p+1} L)^2}\times \frac{\sin\left[\frac{k_{2p+1}L}{2}\right]}{1+\frac{M}{m_c}\sin^2\left[\frac{k_{2p+1}L}{2}\right]} $$
Numériquement, pour $M = 2m_c$, les premiers coefficients valent (en unité de H) : 2.11523, 0.263702, 0.0427238, 0.0248885…
Et sur la figure 4, j’ai représenté des « flashes » de la corde à intervalles réguliers multiples de $T = L/c$, $t_i = i T/5$ avec $i=0,\ 1,\ \dots ,\ 10$. Les courbes en trait plein correspondent aux « flashes » pour les temps défilant de $t=0$ à $t=T$.

Figure 4 Flashes de la corde à intervalles réguliers avec sa masselotte au centre.
Que constate-t-on par rapport au cas d’une corde lâchée de la même manière mais sans masselotte centrale de l’article Oscillations de la corde (Partie I) ?
- la corde se déplace avec la discontinuité de pente au milieu et non pas à plat ;
- la vitesse de la corde n’est pas constante (les flashes sont réalisés à intervalle régulier) avec une montée progressive jusqu’à un maximum ;
- le mouvement n’est plus symétrique par rapport à la position de repos de la corde (cf. l’axe des abscisses) ;
Le premier point est plus satisfaisant qualitativement car le mouvement sans masselotte nous paraissait un peu bizarre par rapport à ce que l’on connaît de ce qui se passe après la décoche.
Pour le second point, j’ai représenté sur la figure 5 l’évolution de la position et de la vitesse du milieu de la corde. Et pour comparé j’ai porté à la fois les résultats que nous venons d’étudier à savoir avec une masselotte $M=2m_c$ au centre et celui sans masselotte rajoutée.
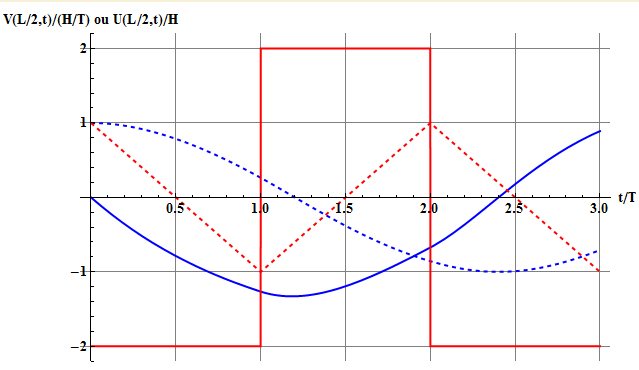
Figure 5 Evolution de la position (courbes en trait plein) et de la vitesse (courbes en trait pointillé) du milieu de la corde dans le cas où il n’y a pas de masselotte supplémentaire (rouge) et une masselotte de masse $M=2m_c$ (bleu). L’unité du temps est T=L/c, de la position H, et de la vitesse H/T.
Sur la photo suivante prise lors du Tournois de Nîmes 2013 par Maxcence Moine de Jesse Broadwater lors de sa décoche. Remarquez dans cette phase de durée 1ms le mouvement de la corde, l’absence de mouvement des branches et de l’archer...
Revenons sur le graphique Figure 5, on voit que
- le moment où la corde passe par sa position de repos (cf. $u(L/2,t)=0$ et repoussé de plus d’un facteur 2 avec une valeur numérique
$ t_0 \approx 1.2 \frac{L}{c} \approx 1.2 \frac{1[m]}{160[m/s]} \approx 7.5ms $ - la vitesse maximale est atteinte également au temps $t=t_0$ avec une valeur de
$ v_0(L/2,t_0) \approx 1.4 \frac{H}{L} c \approx 110 m/s \approx 360 fps $
Si j’avais choisi une masselotte telle que $M=4m_c$, en fait en prenant une corde de 5g, la vitesse $c\approx 220$m/s, le temps caractéristique $T\approx 4.5$ms donnant le temps de passage à la position de repos $t_0\approx 1.6 T \approx 7.3$ms et la vitesse maximale $v_0\approx H/T \approx 110m/s$. Donc $t_0$ et $v_0$ sont relativement insensible au rapport $M/m_c$.
Par contre, soyons un peu plus soigneux au niveau de l’estimation de la tension de corde car en effet avec 50lbs à pleine allonge, en fait par projection avec $H\approx L/2$ on obtient $T_0 \approx 35$lbs soit 155N, ce qui donne une vitesse $c \approx 176$m/s (pour 5g de corde) et donc influe directement sur $t_0 \approx(1.6\times 1)/176 \approx 9$ms et une vitesse $v_0 \approx (0.5/1)\times 176 \approx 88$m/s ou 290 fps.
On est donc dans le bon timing et avec la bonne vitesse d’éjection car en fait le moment où la corde atteint sa vitesse maximale et également le moment où la flèche s’échappe (sauf si l’encoche est trop serrée sur la corde).
Résumé
Dans cet article, j’ai mis en place le formalisme pour étudier le mouvement d’une corde chargée de masselottes ponctuelles. La première masselotte à prendre en compte est celle qui simule la présence de la flèche (!) qui représente typiquement entre 2 et 4 fois la masse totale de la corde placée environ au milieu de la corde. Par rapport au cas sans masselotte, on note un mouvement de corde nettement ralenti et numériquement on peut même rendre compte du temps et de la vitesse de libération de la flèche.
Donc, par la suite j’étudierai l’influence de masselottes placées en bout de corde. A suivre…