Introduction

Cet article est motivée par une discussion par mail avec Pierre-Julien Deloche qui a donné lieu à un article sur son blog, puis à un article soumis au magazine Archery Lifestyle en commun.

De quoi s’agit-il ? Et bien, le collage de nos plumes peut se faire soit dans l’axe de symétrie des tubes ou bien avec un angle (offset en anglais), ou bien encore à utiliser des plumes spiralées sur elle-même (Spin Wing ou bien la future Impulse de chez Bohning). Je me suis demandé quel est l’effet réel de faire tourner sur elle-même la flèche en vol. Plus précisément, cet article répond quantitativement sur la question de la stabilisation gyroscopique ?

Effet gyroscopique : quezaquo

Le plus démonstratif est une vidéo que vous pouvez voir ICI. En fait une simple toupie peut faire l’affaire après l’avoir mis en rotation donner un petit coup perpendiculairement à l’axe de rotation et vous verrez l’axe de la toupie tourner dans un plan horizontal (on dit précession). Si le terme précession, vous dit quelque chose, et bien peut être que vous pensez à la précession des équinoxes (Voir ici qui n’est rien d’autre qu’une manifestation du fait que notre Terre est une grosse toupie...

Bon, l’effet gyroscopique maintient l’axe de la toupie dans une direction précise dans un référentiel inertiel et qu’une perturbation n’entrainera qu’une mise en rotation de ce dernier. Comme dit dans la première Vidéo cela sert en aviation, mais également les torpilles dés la seconde guerre mondiale étaient équipées d’une piéce mobile mise en rotation rapide avant le lancement pour garantir une trajectoire rectiligne de celles-ci. Le canon rayé de certaines armes permettent également la mise en rotation des balles à cette fin. D’où la question : qu’en est-il de nos flèches ?

Stabilisation gyroscopique : est-elle possible ?

Ce n’est pas le lieu de cet article pour développer le formalisme du tenseur d’inertie et l’application du théorème du moment cinétique.
La conséquence directe d’une mise en action de l’effet de stabilisation gyroscopique est que (voir notation sur le schema)

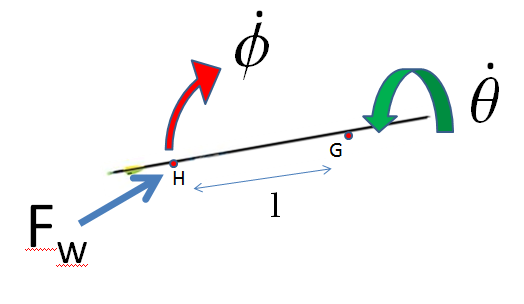
$$ \dot{\phi} \approx \frac{F_{w}l}{J_z \dot{\theta}} $$

avec

• $ \dot{\theta}$  : la vitesse de rotation autour de l’axe principal (supposée suffisamment grande pour que l’effet gyroscopique soit en place) ;
• $ \dot{\phi}$  : la vitesse de rotation dans le plan perpendiculaire non seulement à l’axe de rotation principal mais également à la direction de poussée de la force de perturbation $F_w$ ;
• $F_w$ : une force représentative d’une perturbation latérale. Par exemple on peut considérer un vent de 20 km/h qui donne une force de

$$ F_w = \frac{1}{2}\rho v^2 S \approx \frac{1}{2} \times \left(1.2kg/m^3\right)\times\left(5 m/s\right)^2\times (0.7m)\times(0.01m) \approx 0.12 N $$

qui est d’ailleurs numériquement du même ordre de grandeur que le poids de la flèche (je prends volontairement une grosse flèche !).

• $l$ : une estimation d’une longueur caractéristique du moment exercé par $F_w$ typiquement la longueur entre le centre de poussée et le centre de gravité ($l \approx 50$cm) ;
• $J_z$ le moment d’inertie de la flèche autour de son axe principal. Cette quantité rend compte de la répartition de la masse autour de l’axe. La masse de la flèche est localisée essentiellement dans le fût et la pointe. Typiquement on a un cylindre creux pour le tube, et pour la pointe une partie conique et une partie cylindrique pleine. On calcule alors des moments d’inertie respectifs de l’ordre de (on prend une point de 200 grains, un tube de 300 grains et un diamètre de 9mm)

$$ J_z^{tube} \approx \frac{1}{4}M_{tube}\times D^2 \approx 4.3 10^{-7} kg.m^2 $$

$$ J_z^{pointe}\approx \frac{51}{440}M_{pointe} \times D^2 \approx 1.2 10^{-7} kg.m^2 $$

D’où le moment d’inertie total a une valeur de

$$ J_z \approx 5.5 10^{-7} kg.m^2$$

On constate primo l’extrême faiblesse de cette valeur (exprimée en unité S.I) et secundo le fait que la pointe compte pour 1/5 du total (alors que sa masse compte pour 2/5).

Maintenant que l’on a les ingrédients, mettons tout ensemble à savoir que si la stabilisation gyroscopique avait lieu alors

$$ \dot{\phi} \approx \frac{0.12 N \times 0.5 m}{5.5 10^{-7} kg.m^2 \times \dot{\theta}} \approx \frac{10^5 s^{-2}}{\dot{\theta}} $$

Donc, en principe plus $\dot{\theta}$ est grand (vitesse de rotation sur l’axe grande) plus $\dot{\phi}$ est petit (vitesse de rotation de l’axe dans le plan perpendiculaire).

Mais, le hic vient de l’application en pratique, car imaginons que l’on veuille que notre vent modéré n’affecte notre flèche qu’à raison de $\dot{\phi}\ll 1/10$ tr/s alors il faut imaginer notre flèche tourner sur elle même à la vitesse vertigineuse de $10^6$tr/s !!! Ce qui est totalement exclu !!!

Cela tient à la faiblesse du moment d’inertie de nos flèches et pourtant dans l’application numérique ci-dessus j’ai particulièrement chargé la barque...

Mais en fait ce qui nous importe c’est la façon dont la pointe qui va tourner sur un cône, oscille avec une amplitude trop grande ou non ?
L’expression de l’amplitude en approximation gyroscopique est de l’ordre de

$$ A_w \approx 2 \times \frac{L/2(1-FOC) J_\perp \times (F_w l)}{(J_z \dot{\theta})^2} $$

avec

• $L = 0.7$m et $FOC = 10\%$ la longueur du tube et un FOC typique ;
• $J_\perp \approx 2.5\ 10^{-3}\ kg.m^2$ le moment d’inertie de l’ensemble tube-flèche par rapport à un axe passant par le centre de gravité perpendiculairement à l’axe principal de la flèche. Notons qu’il est plus grand que le moment selon l’axe principal, et on s’en rend compte quand on fait tourner la flèche comme une toupie (par ex. pour vérifier sa rectitude) et quand on joue au majorette...

En mettant tout ensemble, l’amplitude de la pointe serait donnée par

$$ A_w \approx \frac{3\ 10^5\ mm/s^2}{\dot{\theta}^2\ (tr/s)^2} $$

Donc, par exemple si l’on voulait limiter cette amplitude à 1 mm alors il faut que la flèche tourne à plus de [red]550 tr/s[/red] pour cette brise de 20km/h considérée ici. Notons que si le vent double de vitesse d’après ce qui précède, sa force va être multipliée par 4, et il faudrait multiplier par 2 la vitesse de rotation à même amplitude d’oscillations.

Qu’en bien même la contrainte sur l’amplitude est nettement plus modeste que celle de la vitesse de giration, des vitesses de rotation de l’ordre de 500 tr/s ne sont pas envisageables pour autant. Quelques dizaines de tour par seconde à la rigueur. Dans ces cas là, on multiplierait par au moins 100 les effets sur l’amplitude si l’approximation gyroscopique était valable !!!

Epilogue

On conclue que l’usage des empennages hélicoïdaux ou collés à angle ne peuvent en aucun cas stabiliser le vol de nos flèches par effet gyroscopique.

Mais alors sont-ils pour autant inutile ? OUI ! En fait, leur action de faire tourner la flèche permet de répartir les défauts sur 360°, et de changer la trainée en aval donc influe sur le vol mais d’une manière qu’il n’est pas simple de modéliser. Il est donc inévitable de procéder à des essais en vraie grandeur. Pour certaine configuration des archers confirmés ont pu mettre en évidence une amélioration à utiliser des empennages à effet de giration.

Donc à vos empenneuses !