Suite à l’article Passage du 18m à 50m, des mesures sur le terrain ont montré une différence par rapport à la prédiction de positionnement du viseur. Il a fallu le régler non pas à 20mm de la position à 18 m, mais à 25mm.
Ce décalage correspond à une différence de 10% sur l’angle initial de la flèche.
Si le lecteur a déjà parcouru l’article Dynamique d’une flèche en phase de vol (partie IV), il est peut-être curieux de savoir si ce n’est pas du au coefficient de frottement de l’air le long de la trajectoire de la flèche. On sait que ce coefficient est de l’ordre de $10^{-3}\mathrm{m}^{-1} $ mais que sa détermination précise n’est pas aisée (cf. Dynamique d’une flèche en phase de vol (partie III)).
Or, si l’on prend pour hypothèse que le tir à 18m n’est pas affecté par l’air alors on peut écrire en reprenant les notations de l’article Passage du 18m à 50m
$$ d[50]-d[18] = a^{50}\alpha_0[C_b]-a^{18}\frac{g 18}{2v_0^2} $$
avec $\alpha_0[C_b]$ l’expression théorique dépendant du coefficient de frottement, $g = 9.81$ et $v_0 = 54.9$m/s (180 fps pour des 2315).
Le graphe suivant donne la prédiction de $d[50]-d[18]=\Delta d$ en fonction de $C_b$.
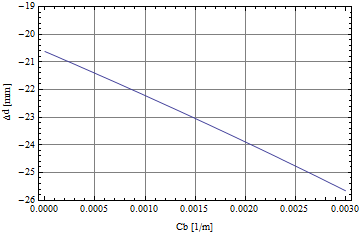
On constate que pour obtenir un décalage de 25mm alors le coefficient de frottement devrait être égal à environ $C_b = 2.5 10^{-3}\mathrm{m}^{-1}$. Ce qui est une valeur dont l’ordre de grandeur est bien celui attendu bien qu’à peu près 2 fois plus grande que celle utilisée dans les articles prospectifs Dynamique d’une flèche en phase de vol (partie III) et Dynamique d’une flèche en phase de vol (partie IV).