Dans l’article Dynamique d’une flèche en phase de vol (partie III), troisième volet d’une série d’articles voués à comprendre le vol d’une flèche, nous avons introduit la force due aux frottements de l’air. Nous avons conclu que cette force pouvait avoir une intensité comparable au poids de la flèche, ce qui n’est pas rien vous en conviendrez. Dans ce nouveau volet nous allons investiguer comment l’équation de la trajectoire est modifiée et estimer les conséquences sur les valeurs de $\alpha_0$.
Raisonnement sur l’énergie
Un des principes de la dynamique que nous avons déjà rencontré, nous fait introduire au coté du poids de la flèche $m \vec{g}$, la force de frottement $\vec{F}_{tr} = - m C_b v^2 \vec{u}_v $ [1]. Il vient donc en utilisant le formalisme différentiel utilisé dans les articles précédents (ici et là) :
$$ \boxed{ m \frac{d\vec{v}}{dt} = m \vec{g} - m C_b v^2 \vec{u}_v }\quad\quad\quad\quad (1) $$
Si on utilise le produit scalaire [2] en multipliant de par et d’autre de l’égalité par $\vec{v}$, on obtient une équation typique sur la variation de l’énergie associée à la flèche à savoir :
$$ \boxed{ \frac{d}{dt} \left( \frac{1}{2} m v^2\right) + \frac{d}{dt}\left( m g y \right) = - m C_b v^3 }\quad\quad\quad\quad (2) $$
On reconnaît dans le premier terme la variation temporelle de l’énergie cinétique, le second terme est la variation de son énergie potentielle de pesanteur. Si on en restait là ($C_b = 0$) alors on conclurait que l’énergie totale, cinétique et potentielle, se conserverait au cours du temps. Or, si $C_b \neq 0$, on a vu que cela donne lieu à des frottements de la surface de la flèche sur l’air, et donc il y a déperdition d’énergie. Ce n’est pas étonnant donc de voir apparaître un signe moins dans le membre de droite de (2) qui traduit la perte d’énergie totale de la flèche. On peut expliquer la composition du membre de droite de l’égalité par un argument d’homogénéité des termes (cf. l’unité dans laquelle ils sont exprimés). $m C_b v^2$ est homogène à une force donc $ m C_b v^2 \times dl$ est homogène à un travail ou une énergie (force x longueur), ainsi $m C_b v^2 \times v$ est homogène à une variation temporelle de travail ou d’énergie comme le membre de gauche de l’égalité.
La nouvelle trajectoire
La trajectoire affectée de la perte d’énergie précitée due aux frottements de la flèche sur l’air, va diverger de la parabole classique étudiée dans Dynamique d’une fléche en phase de vol (Partie I).
Le système d’équations
On projette (1) sur les axes $(x,y)$ [3] car la trajectoire est contenue dans ce plan si la vitesse initiale n’a pas de composante transverse [4] :
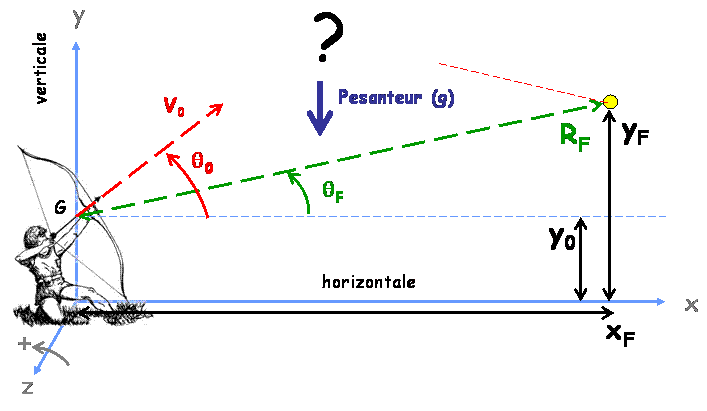
$$ \boxed{ \begin{align*} \ddot{x} & = -C_b\ v\ \dot{x}\\ \ddot{y} & = -g - C_b\ v\ \dot{y} \\ v &= \sqrt{\dot{x}^2+\dot{y}^2} \end{align*} }\quad\quad\quad\quad (2) $$
On rappelle que $\dot{x}$ représente la dérivée première de $x(t)$, tandis que $\ddot{x}$ la dérivée seconde. Les conditions initiales (à $t=0$) sont fixées comme suit
$$ \boxed{ \begin{align*} x(0) & = 0\\ y(0) & = y_0\\ \dot{x} (0) & = v_0 \cos \theta_0 \\ \dot{y} (0) & = v_0 \sin \theta_0 \end{align*} }\quad\quad\quad\quad (3) $$
Notons que si la masse $m$ n’apparaît pas directement dans les équations, elle est présente via non seulement la valeur de la vitesse initiale $v_0$ par la conservation de l’énergie (cf. Dynamique (simple) d’une fléche en phase de propulsion), mais également à travers la valeur du coefficient $C_b$ qui est inversement proportionnel à $m$ (cf. Dynamique d’une flèche en phase de vol (partie III)).
NB : La valeur de $y_0$ sera prise nulle dans les applications numériques suivantes car seul compte la ligne de visée qui ne diffère que de quelque centimètres de la ligne qui joint le centre de gravité de la flèche est le centre de la cible. C’est dans ce but qu’est défini $\theta_f$ à partir du centre de gravité de la flèche et non par rapport au sol.
Une solution ?
Le système d’équations différentielles (2) est un système couplé et non-linèaire : couplé car les équations donnant l’évolution des fonctions $x(t)$ et $y(t)$ dépendent à la fois de $x(t)$ et $y(t)$ à travers la vitesse $v(t)$ ; non-linèaire car la fonction $v(t)$ n’est pas une constante.
Il n’y a pas de solutions algébriques à ce problème si $C_b \neq 0$ ! Si les frottements sur l’air étaient modélisés par une force proportionnelle à la vitesse (et non au carré de celle-ci) alors le problème serait soluble algébriquement. Mais nous savons qu’une force linéaire en fonction de la vitesse n’est pas acceptable dans notre cas car le nombre de Reynolds est bien trop grand pour que nous soyons en régime laminaire (rappel $R_e \approx 5 10^6$ voir Dynamique d’une flèche en phase de vol (partie III)).
Donc, si l’on revient à notre système (2), seul le carré de la vitesse satisfait une équation différentielle dite de Bernouilli qui est soluble exactement (Leibniz 1696), mais cela ne nous aide pas dans notre cas car nous voulons décrire la trajectoire complètement afin de déterminer l’orientation initiale de la flèche pour quelle atteigne son but…
Notons que la résolution approchée de ce problème (par exemple sous forme de série en puissance de $C_b$) fait encore partie des domaines de recherche en mathématique appliquée étant donné le caractère sensible de ses applications : lancement de projectiles… On note par example la publication récente : P.S Chudinov, « The motion of a point mass in a medium with a square law of drag »
J. Appl. Maths Mechs, Vol. 65, No. 3, pp. 421-126, 200. [5]. Cependant pour avoir utiliser cet publication dans le but de préparer cet article, les approximations fournies ne sont pas suffisamment précises [6].
Résolution numérique
Nous allons donc procéder à une résolution numérique du système d’équations (2) avec les conditions initiales (3). Pour se faire, il est nécessaire de faire appel à un utilitaire d’intégration comme Mathematica qui permet par exemple de donner les courbes suivantes montrant la différence entre les trajectoires suivies par la flèche en présence des forces de frottement ou non.
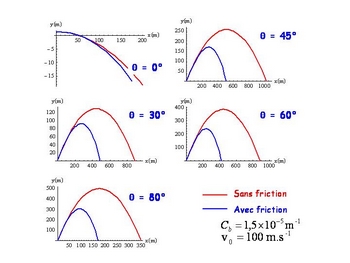
On note tout de suite que la portée du tir est affectée ainsi que l’altitude maximum. Si on y regarde de plus prés on note également que la courbe n’est plus symétrique par rapport au maximum, comme l’est la parabole.
L’angle initial de la flèche
Comme dans l’article Dynamique d’une fléche en phase de vol (Partie II), nous allons maintenant nous intéressé à la détermination de l’angle $\alpha_0$ que fait la flèche avec la direction de visée, comme définit sur la figure suivante :
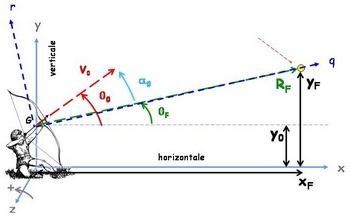
La méthode
L’algorithme pour trouver $\alpha_0$ connaissant la vitesse initiale $v_0$ de la flèche et la position relative de la cible donnée par le couple $(\theta_f, R_f)$, tout en tenant compte de la pesanteur ($g = 9.81\ \mathrm{m.s}^{-2}$) et des frottements de l’air $C_b$, peut s’écrire schématiquement comme suit :
- fixer les valeurs de $v_0$, $\theta_f$, $R_f$, $g$, $C_b$ ;
- changer de repère $(x,y)$ en $(q,r)$ centré sur le départ de la flèche en direction de la cible ($q$), le nouveau système d’équations couplées donnent $q(t)$ et $r(t)$ ;
- chercher $t_f[\alpha_0]$, fonction implicite de $\alpha_0$, tel que $r(t_f[\alpha_0]) = 0$ ;
- chercher $\alpha_0$ tel que $q(t_f[\alpha_0]) = R_f$.
Pour les personnes intéressées, la mise en forme de l’algorithme dans Mathematica est décrite dans l’Annexe.
Des valeurs pour des altitudes positives
La table suivante donnent pour différentes valeurs de $R_f$ (10m à 70m) et de $\theta_f$ ($0^\circ$ à $80^\circ$), les valeurs de $\alpha_0$ en mrad ($v0 = 300\ \mathrm{fps} = 91.25 \mathrm{m.s}^{-1}$ et $C_b = 1.5 10^{-3} \mathrm{m}^{-1}$ valeur typique obtenue dans l’article Dynamique d’une flèche en phase de vol (partie III))
| $R_f (m)$$\theta_f ({}^\circ)$ | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 10 | 5.9 | 5.8 | 5.6 | 5.1 | 4.6 | 3.8 | 3.0 | 2.0 | 1.0 |
| 20 | 12.0 | 11.8 | 11.3 | 10.4 | 9.2 | 7.8 | 6.0 | 4.1 | 2.1 |
| 30 | 18.1 | 17.9 | 17.2 | 15.9 | 14.1 | 11.8 | 9.2 | 6.3 | 3.2 |
| 40 | 24.4 | 24.2 | 23.2 | 21.4 | 19.0 | 16.0 | 12.5 | 8.6 | 4.4 |
| 50 | 30.9 | 30.6 | 29.3 | 27.2 | 24.1 | 20.3 | 15.9 | 10.9 | 5.5 |
| 60 | 37.4 | 37.1 | 35.7 | 33.1 | 29.4 | 24.8 | 19.4 | 13.3 | 6.8 |
| 70 | 44.1 | 43.8 | 42.1 | 39.1 | 34.9 | 29.4 | 23.0 | 15.8 | 8.0 |
On constate que plus la cible se trouve en altitude, plus l’angle $\alpha_0$ est proche de $0$ (comme si la flèche devait sortir "horizontalement", selon la direction de la pente). On peut comparer numériquement les valeurs ci-dessus, à celles obtenues sans tenir compte des frottements de l’air en calculant les différences :
| $R_f (m)$$\theta_f ({}^\circ)$ | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 10 | 0.1 | 0.1 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 20 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.1 | 0.1 | 0.0 |
| 30 | 0.5 | 0.5 | 0.5 | 0.5 | 0.4 | 0.4 | 0.3 | 0.2 | 0.1 |
| 40 | 1.0 | 1.0 | 0.9 | 0.9 | 0.8 | 0.7 | 0.5 | 0.4 | 0.2 |
| 50 | 1.5 | 1.5 | 1.5 | 1.4 | 1.2 | 1.0 | 0.8 | 0.6 | 0.3 |
| 60 | 2.2 | 2.2 | 2.2 | 2.0 | 1.8 | 1.5 | 1.2 | 0.8 | 0.4 |
| 70 | 3.0 | 3.1 | 3.0 | 2.8 | 2.5 | 2.1 | 1.7 | 1.2 | 0.6 |
On constate que les valeurs de $\alpha_0$ dans l’air sont plus grandes que celles sans air, et cela d’autant plus que la cible est à longue distance et à l’horizontale.
Graphiquement, pour $\theta_f=10^\circ$ (rouge) et $\theta_f=60^\circ$ (bleu), la valeur de $\alpha_0$ dépend quasi-linéairement de $C_b$ dans la zone considérée comme le montre le graphique suivant :

Vous me direz que peut bien faire un effet de 3 mrad sur le vol d’une flèche à 70 m ! L’archer averti se dit que cela correspond à 3 mm pour un viseur situé à 1 m de l’œil donc l’effet doit être significatif… Et il a raison ! Graphiquement on peut matérialiser l’erreur que ferait un archer qui voudrait utiliser des valeurs de $\alpha_0$ calculées sans tenir compte de l’air pour différentes distances de cibles et pour des angles $\theta_f$ variables.
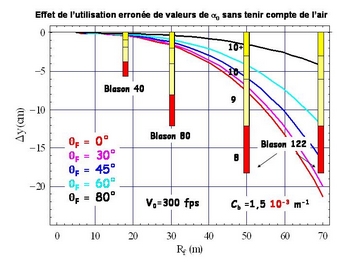
A partir de 30 m, pour un tir horizontal, on sortirait du 10+. Par contre, à 18 m indépendamment de l’angle de visée on ne sort pas du 10+ et tenir compte de l’air peut paraître superflue. Enfin, plus la cible est située en hauteur ou en dévers, moins tenir compte de l’air se fait sentir. Cela tient au fait que la courbe est particulièrement différente de la parabole après le maximum, or en hauteur/dévers le but est atteint avant le maximum.
Des valeurs pour des altitudes négatives (en dévers)
Pour les cibles en dévers ($\theta_f <0$), la table suivante donne les valeurs de $\alpha_0$ dans les mêmes conditions que précédemment avec la valeur de $C_b = 1.5 10^{-3} \mathrm{m}^{-1}$.
| $R_f (m)$$\theta_f ({}^\circ)$ | 0 | -10 | -20 | -30 | -40 | -50 | -60 | -70 | -80 |
| 10 | 5.9 | 5.8 | 5.6 | 5.1 | 4.5 | 3.8 | 2.9 | 2.0 | 1.0 |
| 20 | 12.0 | 11.8 | 11.2 | 10.3 | 9.1 | 7.6 | 5.9 | 4.0 | 2.1 |
| 30 | 18.1 | 17.8 | 16.9 | 15.6 | 13.7 | 11.5 | 8.9 | 6.1 | 3.1 |
| 40 | 24.4 | 24.0 | 22.8 | 20.9 | 18.4 | 15.4 | 12.0 | 8.2 | 4.1 |
| 50 | 30.9 | 30.2 | 28.7 | 26.3 | 23.2 | 19.4 | 15.0 | 10.3 | 5.2 |
| 60 | 37.4 | 36.6 | 34.7 | 31.8 | 28.0 | 23.4 | 18.1 | 12.4 | 6.3 |
| 70 | 44.1 | 43.1 | 40.8 | 37.4 | 32.9 | 27.4 | 21.2 | 14.5 | 7.3 |
On note une très grande similitude avec valeurs déterminées pour $\theta_f>0$ telles que $\alpha_0(\theta_f) \approx \alpha_0(-\theta_f)$, cependant moins vérifiée pour les grands angles $\theta_f$.
L’effet de l’entraînement à l’horizontal
Les archers dont les disciplines sont les parcours Nature, Campagne ou 3D n’ont pas forcément la chance de s’entraîner en situation avec des cibles en hauteur ou en dévers… Ils doivent se contenter de cibles à différentes distances certes mais à partir d’une certaine distance elles sont toutes quasiment à l’horizontale. Est-ce grave docteur ? Et bien la réponse dépend de votre objectif. Voici un graphique qui montre pour trois distances $R_f = 20, 30, 50$ m, l’évolution de l’offset $\Delta r$ (exprimé en cm) en fonction de l’angle $\theta_f$ auquel se trouve la cible. $\Delta r$ est nul si la flèche arrive à son but au milieu, il est positif si la flèche touche la cible au dessus du milieu et il est négatif dans le cas où la flèche touche la cible en dessous du milieu.
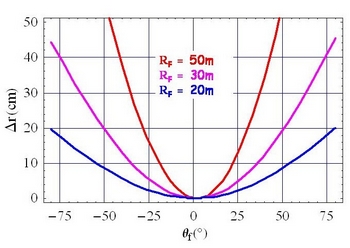
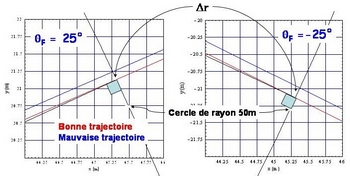
L’effet est redoutable, n’est-ce pas ! Il est à noter qu’à des pouillèmes prés les graphiques sont identiques à ceux obtenus sans tenir compte de l’air ! Le graphique ci-dessous présente deux cas de figures symétriques $\theta_f = \pm 25^\circ$. Le trait noir (rayon) indique la direction de tir vu de l’archer placé à 50 m de la cible, il coupe le cercle de rayon 50 m à angle droit (matérialisé par le carré bleu clair) comme il se doit. Le trait rouge correspond à la trajectoire de la flèche calculée avec un angle $\alpha_0$ déterminé pour la direction en considération. On vérifie que la trajectoire rouge coupe bien le cercle à l’intersection avec le rayon noir, elle a été calculée pour réaliser cette propriété. Maintenant, si on utilise une valeur de $\alpha_0$ calculée certes pour la même distance de 50 m mais à l’horizontale, on obtient la trajectoire bleue qui diffère de la trajectoire rouge d’un offset $\Delta r$. Dans les deux cas, la trajectoire bleue rate le but par le haut. Maintenant à vous de voir si rater la cible de 15 cm ça vous convient…
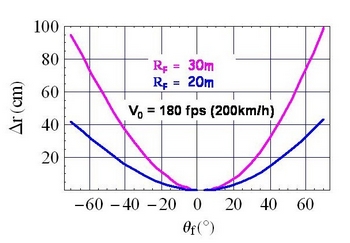
Le même type de graphique que "Usage erroné des valeurs de $\alpha_0 (0^\circ)$ pour des valeurs de $\theta_f$ différentes de $0^\circ$" mais cette fois calculé avec une vitesse initiale de flèche de 180 fps (200 km/h) au lieu de 300 fps montre des offsets encore plus importants comme on peut en juger sur le graphique, ci-dessous :
En pratique ?
Vous me direz tout ça c’est bien joli, mais comment puis-je m’en servir ? Cette question pertinente en cache plusieurs.
Réglage du viseur
On peut d’abord se demander connaissant les valeurs de $\alpha_0$ comme celles des tables précédentes, quel réglage de mon viseur dois-je opérer ? En fait c’est relativement simple car le réglage du viseur et l’angle $\alpha_0$ sont relier par la formule simple suivante (pour les angles petits) :
$$ d - d^{10} = - a \times (\alpha_0 - \alpha_0^{10}) $$
où $ d^{10}$ et $\alpha_0^{10}$ sont les valeurs de références à 10 m (à l’horizontale par exemple). Comme on peut le voir sur la figure suivante
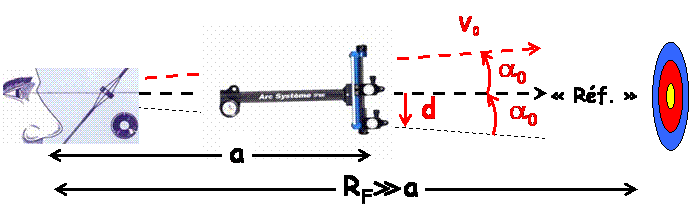
$a$ est la distance œil-viseur et le signe "$-$" indique que si l’on veut faire monter la flèche il faut descendre le viseur afin que dans la position de visée œil-viseur-cible la flèche soit effectivement plus inclinée vers le haut que dans la position de référence. On apprend en principe cela lors de l’initiation au tir à l’arc n’est-ce pas ?
Ainsi,
- il faut se placer à 10 m (ou bien à une autre distance de référence),
- mesurer sur l’échelle verticale la cote $d^{10}$ qui permet d’envoyer la flèche au centre de la cible,
- mesurer la distance oeil-viseur ($a$) en se faisant aider d’un autre archer si possible,
et le tour est joué, on applique la formule ci-dessus en reportant la différence des angles $\alpha_0$ (nouvelle distance - référence) du membre de droite qui permet de déterminer la valeur $d$ connaissant $d^{10}$.
La détermination des tables d’angles
Mais vous me direz, comment puis-je savoir si les tables de cet article me conviennent ? En principe, elles ont toutes les chances de ne pas convenir ! En effet, il faut être sûre que vous vous trouviez dans la même configuration des paramètres ayant servi à leur établissement : $v_0$ la vitesse initiale de la flèche qui va dépendre de la puissance de votre arc et de la masse de la flèche (cf. Dynamique (simple) d’une fléche en phase de propulsion), et $C_b$ le coefficient balistique qui dépend de la géométrie et de l’état des surfaces (cf. Dynamique d’une flèche en phase de vol (partie III)).
Pour ce qui concerne $v_0$, on a recours en principe à un tachymétre (radar) comme celui de la photo suivante :
Pour ce qui concerne $C_b$ c’est moins immédiat. On peut essayer d’estimer la valeur selon la géométrie de la flèche et de son état de surface. Par contre, si on a un grand terrain (plusieurs centaines de mêtres...), on peut se servir de la mesure de la portée du tir (il ne faut pas de vent) $L$ et les expressions approchées suivantes (dues à P.S. Chudinov) pour extraire $C_b$ :
$$ \begin{align*} L &\approx V_m \times T \\ V_m &= v_0 \cos \alpha_0/\sqrt{1 + (C_b/g) v_0^2 \cos^2 \alpha_0 f(\alpha_0)}\\ f(x) &= \sin x/\cos^2 x + \log \left[ \tan \left( \frac{x}{2} + \frac{\pi}{4} \right) \right]\\ T &\approx 2 \sqrt{\frac{2 H}{g}} \\ H &\approx v_0^2 \sin^2 \alpha_0/(2 g + C_b v_0^2 \sin\alpha_0)\\ \end{align*} $$
Les variables morphologiques de la trajectoire sont définis sur la figure ci-dessous :
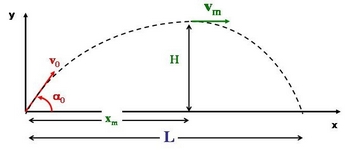
avec $T$ le temps de parcours de la flèche.
Résumé et perspective
Dans cet article, nous avons mis en valeur l’effet de l’air (via le coefficient balistique) sur la trajectoire de la flèche, et montré la nécessité d’en tenir compte sous peine de grossière erreur. Nous avons également montré comment déterminer les paramètres qui permettent de calculer l’angle d’incidence de la flèche.
Pour aller plus loin encore dans la compréhension du mouvement de la flèche, il faudrait prendre en compte :
- l’effet de portance des empennages ;
- l’effet gyroscopique éventuelle engendré par ces derniers (usage des spin-wing et/ou d’empennages collés à angle) ;
- les effets du vent ;
- et enfin la souplesse de la flèche lors de la propulsion
- les effets de poussées non correctes lors de la propulsion
- les effets de couple lors de la tenue de l’arc
- des effets d’angle par rapport à la verticale agissant sur le latéral...
On peut néanmoins se demander si l’on peut/veut tout vouloir modéliser. Il est vraisemblable que des arguments avec les mains puissent suffire à dégager les notions. Qui plus est l’archer aguerri par les compétitions sait que seul les mesures faites sur le terrain servent à quelque chose. Surtout que depuis peu Franck Karsenty a mis au point un instrument qui permet :
- de régler la sortie de flèche
- d’aligner la flèche pour quelle puisse subir une poussée linéaire optimale lors du décochage
- surveiller les paramètres de temps en temps
- de travailler la pression sur le grip
En définitive tous ces éléments agissent sur le latéral, domaine que nous n’avons pas abordé dans notre série d’articles.
Ceci dit, chacun peut réagir à l’ensemble des articles de la série...
Annexe
Pour les personnes intéressées, voici la mise en œuvre du code que l’on peut directement utiliser dans un Notebook de Mathematica (v4 et supérieure) qui permet de déterminer la valeur de $\alpha_0$ fonction de $v_0$, $\theta_f$, $R_f$, $g$ et $C_b$ :
alpha[v0_,qf_,Rf_,g_,Cb_] := (
tfinal[a0_] := (
sol = NDSolve[{
q''[t] == - g Sin[qf] -Cb q'[t]Sqrt[q'[t]^2 + r'[t]^2],
r''[t] == -g Cos[qf] - Cb r'[t]Sqrt[q'[t]^2 + r'[t]^2],
q[0] == 0, r[0] == 0,
q'[0] == v0 Cos[a0], r'[0] == v0 Sin[a0]}, {q, r}, {t, 0, 40}];
rr[t_] = r[t] /. sol[[1]]; qq[t_] = q[t] /. sol[[1]];
t /. FindRoot[rr[t] == 0, {t, 1/10, 5}]
);
qfinal[a0_?NumericQ] := qq[tfinal[a0]];
a0 /. FindRoot[qfinal[a0] == Rf, {a0, 0, 0.1}]
)Ensuite pour constituer une table comme celles des sections précédentes on utilise le code suivant par exemple donnant les valeurs pour $R_f$ de 10m à 70m par pas de 10m, et $\theta_f$ de $0^\circ$ à $80^\circ$ par pas de $10^\circ$ :
TextForm[PaddedForm[
TableForm[
Table[1000*alpha[91.45,0.,qf,Rf,9.81,0.0015] "|",
{Rf,10,70,10},{qf,0,80*Pi/180,10*Pi/180}],
TableHeadings \[Rule] {Table[i "|",{i,10,70,10}],
Table[i "|",{i,0,80,10}]}, TableSpacing\[Rule]{1,1}],{4,1}]]Connaître l’offset $r$ pour une configuration de $\alpha_0$, $v_0$, $\theta_f$, $R_f$, $g$ et $C_b$ se calcule de la façon suivante :
rfinal[a00_,v0_,qf_,Rf_,g_,Cb_]:=
(
tfinal[a0_]:=(sol=
NDSolve[{
q''[t]== -g Sin[qf] -Cb q'[t]Sqrt[q'[t]^2+r'[t]^2],
r''[t]==-g Cos[qf]-Cb r'[t]Sqrt[q'[t]^2+r'[t]^2],
q[0]==0,r[0]==0,
q'[0]==v0 Cos[a0],r'[0]==v0 Sin[a0]},{q,r},{t,0,40}];
rr[t_]=r[t]/.sol[[1]];qq[t_]=q[t]/.sol[[1]];
t /. FindRoot[qq[t]\[Equal]Rf,{t,1/10,10}, MaxIterations\[Rule]20]
);
rr[tfinal[a00]]
)





























Commentaires Forum fermé