Introduction
Dans l’article Dynamique d’une fléche en phase de vol (Partie I), première partie d’une série, nous avons jeter les bases pour appréhender la trajectoire de la flèche après sa phase de propulsion (Dynamique (simple) d’une fléche en phase de propulsion). Nous en avions conclu que la flèche (plus exactement son centre de gravité) décrit une parabole (Différentes trajectoires paraboliques) dans le cas où l’on néglige les frottements de l’air. Dans le présent article, nous allons mettre en application ce résultat en envisageant des configurations concrètes.
Atteindre son but
L’expression de l’équation de la trajectoire de la flèche peut être utilisée pour répondre à différentes questions :
- connaissant la position d’un but à atteindre et les paramètres initiaux de position verticale et vitesse de la flèche ($y_0$, $v_0$) quelle est la valeur de l’angle $\theta_0$ de la vitesse par rapport à l’horizontale pour réussir à toucher l’objectif ?
- inversement connaissant les paramètres initiaux ($y_0$, $\theta_0$, $v_0$) quelle est la position de la flèche à une distance fixée (de combien on rate l’objectif) ;
- etc
Dans cet article nous allons nous intéresser à la première question, laissant la seconde pour une étude ultérieure où seront intégrés des éléments de l’interaction flèche-air. On repère l’objectif (Repère des positions et des angles) par au choix ($\theta_F$, $R_F$) ou ($x_F$, $y_F$) avec une relation entre ces deux représentations :
$$ \begin{align*} x_F &= R_F \cos \theta_F \\ y_F &= R_F \sin \theta_F \\ R_F &= \sqrt{x_F^2 + y_F^2}\\ \theta_F & = \arctan(x_F/y_F) \\ | \theta_F | & \leq \pi \quad (\pi \leftrightarrow 180^\circ) \end{align*} $$
Ainsi, si l’archer atteint son but alors la relation suivante est satisfaite (cf. Eq.21) :
$$ \boxed{ \frac{y_F-y_0}{y_m-y_0} = 2 \frac{x_F}{x_m}\left( 1 - \frac{x_F}{2x_m}\right) } \quad\quad\quad\quad (1) $$
Imaginons que l’archer puisse décocher une flèche avec une vitesse infinie (monsieur muscles en quelque sorte !), alors l’expression générale de la trajectoire (cf. Eq.18)
$$ Y = y_0 + \tan \theta_0 X - \frac{1}{2} \frac{g}{v_0^2\cos^2\theta_0} X^2 \quad\quad\quad\quad (2) $$
montre que dans ce cas le dernier terme est nul et donc que la trajectoire est purement rectiligne sans courbure. Il est légitime dans ces conditions que l’archer vise en ligne droite l’objectif. Donc, dans ce cas limite
$$ \theta_0 = \theta_F \quad\quad (v_0 = \infty) $$
Mais la réalité est tout autre ! Et oui, on fait avec ce que l’on a dans ce bas monde. Cependant, on peut poser en toute généralité que la solution $\theta_0$ qui permet à l’archer d’atteindre son but, soit de la forme
$$ \boxed{ \theta_0 = \theta_F + \alpha_0 }\quad\quad\quad\quad (3) $$
Le cas d’une vitesse infinie se traduit alors par $\alpha_0 = 0$.
L’expression de $\alpha_0$ découle de (1) en utilisant les expressions (polaires) de $x_F$ et $y_F$ et celles de $x_m$ et $y_m$ (cf. Eq.20)
$$ \boxed{ \frac{\tan \theta_F}{\tan(\theta_F + \alpha_0)} = 1 - \frac{g R_F}{v_0^2} \frac{\cos \theta_F}{\sin 2(\theta_F + \alpha_0)} } \quad\quad\quad\quad (4) $$
A l’horizontale
Pour appréhender la solution donnant $\alpha_0$ en fonction de $R_F$ et $\theta_F$ à vitesse fixée mettons nous sur un plan horizontal tel que $\theta_F = 0$. Dans ce cas $\theta_0$ et $\alpha_0$ sont confondus et l’on note la valeur $\alpha_0^H$. La condition de succès (4) impose que l’archer tienne son arc de telle façon que
$$ \boxed{ \sin 2 \alpha_0^H = \frac{g R_F}{v_0^2} } \quad\quad\quad\quad (5) $$
Etant donné que $\sin 2 \alpha_0^H \leq 1$
par définition du sinus d’un angle, l’existence même d’une solution, est qu’il y a une vitesse minimum égale à
$$ \boxed{ v_0^{lim} \geq \sqrt{g R_F} } \quad\quad\quad\quad (6) $$
Et oui ! bien qu’une vitesse infinie ne soit pas nécessaire, il faut qu’en même une certaine puissance d’arc. La table ci-dessous fixe les ordres de grandeurs
| $R_F$ (m) | $v_0^{lim} $ (m/s) | $v_0^{lim} $ (fps) |
| 18 | 13 | 43 |
| 30 | 17 | 56 |
| 50 | 22 | 72 |
| 70 | 26 | 85 |
| 100 | 31 | 101 |
Le lecteur assidu de l’article Dynamique (simple) d’une fléche en phase de propulsion en conclurait : qu’avec un simple arc d’initiation, on arrive sans peine à faire du FITA. « Y-a comme un truc qui dirait » ! Même au niveau d’approximation à propos des frottements dus à l’air, l’archer qui ne tirerait qu’à la vitesse limite verrait sa flèche venir tout juste atteindre objectif, et la précision sur l’angle initial devrait être infinie sous peine de rater le but. Egalement, nous avons toutes et tous l’expérience (intuition) qu’il faut un peu plus de pêche pour atteindre le but et que négliger l’air a ces limites. Mais de cela nous y reviendrons dans un article ultérieur. Donc attention aux conclusions hâtives : il faut se précipiter lentement...
Fixons, la vitesse $v_0 = 300$ fps (soit 91.45 m/s) c’est-à-dire la vitesse initiale d’une flèche IBO (350 grains) tirée par un arc qui développe une énergie d’environ 95 J, c’est-à-dire par exemple un arc à poulie d’environ 50 lbs au pic (Dynamique d’une fléche en phase de vol (Partie I)). Le graphe ci-dessous montre l’évolution de $\alpha_0^H$ en fonction de la distance à la cible $R_F$</math (rappel : située à la même hauteur/altitude que le point de départ de la flèche)

La courbe $\alpha_0^H (R_F)$ semble manifester une relation de proportionnalité dans les conditions de cet exercice. Ceci se démontre facilement, car pour $v_0 \gg v_0^{lim}$ (c’est notre cas), alors la relation (5) permet d’écrire l’approximation [1]
$$ \alpha_0^H (R_F) = \frac{1}{2} \left( \frac{v_0^{lim}}{v_0} \right)^2 + \dotsb $$
où on à négligé des termes d’ordre $\mathcal{O} (v_0^{lim}/v_0)^4$ (ex. une correction bien inférieure à 10% dans notre exemple). Ainsi, en injectant l’expression de la vitesse limite, on obtient
$$ \alpha_0^H (R_F) \approx \frac{g}{2 v_0^2} R_F \quad\quad\quad\quad (7) $$
ce qui démontre la relation de proportionnalité.
Si la valeur de la vitesse initiale est male estimée (cf. mauvaise estimation de la puissance de l’arc, allonge irrégulière,…) alors il est légitime de se poser la question de la sensibilité de la valeur de $\alpha_0^H (R_F)$. Le graphe ci-dessous donne les différences entre la valeur de référence de $\alpha_0^H$ pour une vitesse $v_0 = 300$ fps et la valeur de $\alpha_0^H$ calculée dans le cas où la vitesse varie de $\pm 2,5$%, $\pm 5,0$% (cf. une variation typique de $\pm 5$%, $\pm 10$% de la puissance d’un arc à poulie)
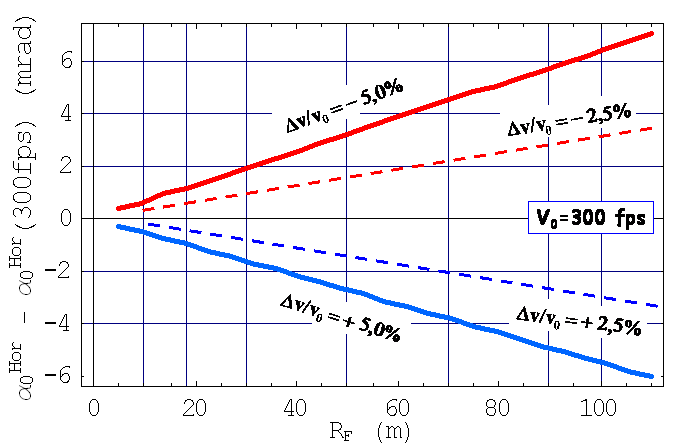
Ces variations sont simples à comprendre à l’aide de l’expression approchée ci-dessus par la variation relative d’une loi de puissance (ici $\alpha_0^H$ varie selon $1/v_0^2$) :
$$ \frac{\Delta \alpha_0^H}{\alpha_0^H(300 fps)} \approx - 2 \frac{\Delta v_0}{v_0} $$
D’où l’on justifie les écarts de 5% à 10% sur $\alpha_0^H$. En anticipant un peu sur une discussion plus approfondie, on peut apprécier ces résultats préliminaires plutôt en terme de réglages de viseur qui se traduisent par des décalages verticaux gradués en mm. Or, 1 mrad est l’angle sous lequel on voit un objet de 1 mm de hauteur placé à 1 m, ou bien un objet de 0,5 mm à 50 cm. Donc le décalage vertical est fonction de la position du viseur. Soit par exemple un viseur à 1 m de l’œil. Donc pour $\alpha_0^H = 30$ mrad (cf. à 50 m) cela se traduit par un réglage du viseur de -30 mm (vers le bas si on veut monter l’arc). Une variation de +2,5% de la vitesse (300 fps -> 307,5 fps) induit une variation de -5% d’angle, et donc -5% sur le réglage soit -1,5 mm. Il faut remonter le viseur de 1,5 mm (1 division 1/2) ce qui est tout à fait sensible comme on le verra dans un article ultérieur sur la précision de l’impact en cible…
Pour un angle quelconque
En examinant l’équation (4), nous pouvons y introduire l’expression (5), il vient alors
$$ \boxed{ \frac{\tan \theta_F}{\tan(\theta_F + \alpha_0)} = 1 - \cos \theta_F \frac{\sin 2 \alpha_0^H}{\sin 2(\theta_F + \alpha_0)} } \quad\quad\quad\quad (8) $$
Ainsi, pour un angle quelconque $\theta_F$, il y a une relation entre le supplément d’angle initial $\alpha_0$ de la flèche (3), et l’angle quelle devrait avoir dans le cas horizontal. Cette situation est intéressante pour les archers s’entraînant en général sur des terrains plats et évoluant dans des disciplines de parcours (Campagne, 3D).
Soit le schéma suivant qui fixe les conventions de notations des angles.

Alors, on peut :
- soit s’intéresser à la valeur de $\epsilon$ qui représente la correction à une mise en application d’un réglage comme si l’archer se trouvait à l’horizontale mais avec une cible à angle $\theta_F$. Rappelons dans ce cas que la direction initiale de la flèche par rapport à l’horizontale est
$$ \theta_0 = \theta_F + \alpha_0^H + \epsilon $$
- soit s’intéresser à la valeur de $\alpha_0$ qui représente directement le réglage angulaire à opérer pour différentes distances $R_F$ et différentes incidences $\theta_F$. Dans ce cas la direction initiale de la flèche est (3)
$$ \theta_0 = \theta_F + \alpha_0 $$
La figure suivante présente différentes situations de $\theta_F =$ ($2^\circ$, $8^\circ$, $16^\circ$, $25^\circ$, $30^\circ$, $45^\circ$, $60^\circ$, $70^\circ$, $80^\circ$) afin de déterminer la valeur de $\epsilon$ en fonction de $\alpha_0^H$. Les trois premières valeurs angulaires sont approximativement les situations correspondantes aux angles sous-tendus par 1 pouce, 1 main horizontale, 1 main verticale à bras tendu.
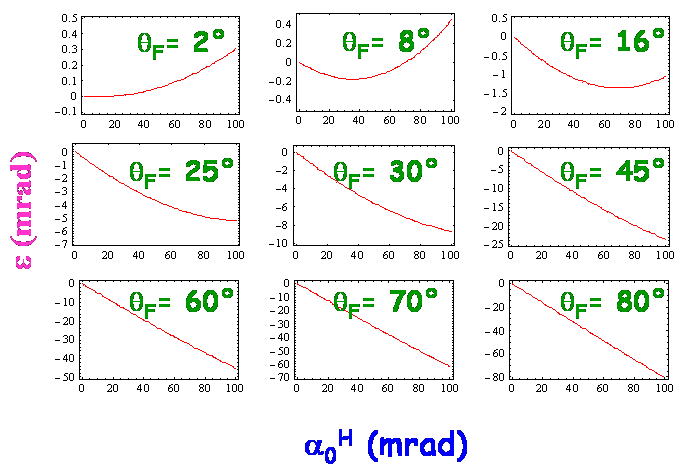
Nous constatons que pour $\theta_F \leq 16^\circ$ la correction $\epsilon$ à un réglage fait sur l’horizontal est inférieure ou de l’ordre de 1%, que jusqu’à $\theta_F\leq 30^\circ$ cette correction est inférieure à 10% et qu’ensuite elle augmente de plus en plus pour atteindre 100% à la verticale. Cette évolution est bien naturelle, d’ailleurs dans le cas d’une cible à la verticale, il suffit de faire un réglage à l’horizontal avec le viseur à "$0$" matérialisant horizontal et de pointer la verticale (attention il faut se sauver) ! En effet, dans ces conditions le mouvement de la flèche se fait parallèlement à la pesanteur... Ainsi si on procède à un réglage de viseur comme si la situation à angle était identique celle à l’horizontale, il faudrait en quelque sorte annuler ce réglage et donc la correction $\epsilon$ serait égale à $ - \alpha_0^H$ $(\theta_F = 90^\circ)$.
L’évolution de $\epsilon$ en fonction de $\theta_F$ nous incite donc à donner directement l’évolution de $\alpha_0$ pour les grandes valeurs de $\theta_F$.
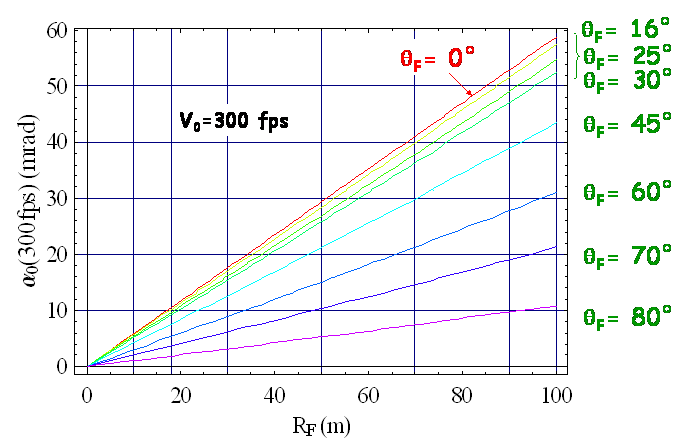
La courbe rouge correspond bien au cas horizontal présenté sur la figure Angle initial de la flèche (tir à "l’horizontal" ; sans frottement). D’ailleurs au même titre que nous avions déterminé l’expression (7) approchée de $\alpha_0^H$, voici l’expression approchée de $\alpha_0$ pour un angle $\theta_F$ quelconque poussée à un ordre $(v_0^{lim}/v_0)^4$
$$ \alpha_0 (R_F) \approx \frac{gR_F}{2 v_0^2} \cos \theta_F + \frac{g^2 R_F^2}{4 v_0^4} \sin\theta_F \cos\theta_F \quad\quad\quad\quad (9) $$
(En passant, on montre que pour $\theta_F=0$ (horizontale) les termes en $(v_0^{lim}/v_0)^4$ proportionnel à $R_F^2$ sont nuls ce qui justifie encore mieux l’approximation (7) dans ce cas.)
La table suivante donne des valeurs numériques de $\alpha_0$ en mrad pour différentes valeurs de $R_F$ et de $\theta_F\geq 0$ et pour $v_0 = 300$ fps. Les valeurs à 10 m sont absolues, tandis qu’au-delà les valeurs sont relatives. Par exemple, la valeur de 5.0 mrad donnée pour $R_F = 20$ m et $30^\circ$ est relative à l’angle de 5.1 mrad donné également pour $30^\circ$ mais à $R_F = 10$ m, en d’autres termes à part la première ligne, les autres valeurs de la table donnent $\alpha_0(R_F,\theta_F) - \alpha_0(10 m, \theta_F)$. Ces valeurs relatives sont plus faciles d’accès car en général on peut disposer des réglages absolus à 10 m (ou autres faibles distances) directement en visant une cible sans avoir un repérage de l’horizontal.
| $R_F/\theta_F$ | $0^\circ$ | $10^\circ$ | $20^\circ$ | $30^\circ$ | $40^\circ$ | $50^\circ$ | $60^\circ$ | $70^\circ$ | $80^\circ$ |
| Valeurs absolues | |||||||||
| 10 m | 5.9 | 5.8 | 5.5 | 5.1 | 4.5 | 3.8 | 2.9 | 2.0 | 1.0 |
| Valeurs relatives | |||||||||
| 15 m | 2.9 | 2.9 | 2.8 | 2.6 | 2.3 | 1.9 | 1.5 | 1.0 | 0.5 |
| 20 m | 5.9 | 5.8 | 5.5 | 5.1 | 4.5 | 3.8 | 3.0 | 2.0 | 1.0 |
| 25 m | 8.8 | 8.7 | 8.3 | 7.7 | 6.8 | 5.7 | 4.5 | 3.1 | 1.6 |
| 30 m | 11.7 | 11.6 | 11.1 | 10.3 | 9.1 | 7.7 | 6.0 | 4.1 | 2.1 |
| 35 m | 14.7 | 14.5 | 13.9 | 12.9 | 11.4 | 9.6 | 7.5 | 5.1 | 2.6 |
| 40 m | 17.6 | 17.4 | 16.7 | 15.5 | 13.7 | 11.6 | 9.0 | 6.2 | 3.1 |
| 45 m | 20.5 | 20.3 | 19.5 | 18.1 | 16.1 | 13.5 | 10.6 | 7.2 | 3.7 |
| 50 m | 23.5 | 23.2 | 22.3 | 20.7 | 18.4 | 15.5 | 12.1 | 8.3 | 4.2 |
| 55 m | 26.4 | 26.2 | 25.1 | 23.3 | 20.7 | 17.5 | 13.6 | 9.4 | 4.8 |
| 60 m | 29.3 | 29.1 | 27.9 | 25.9 | 23.1 | 19.4 | 15.2 | 10.4 | 5.3 |
| 65 m | 32.3 | 32.0 | 30.8 | 28.6 | 25.4 | 21.4 | 16.7 | 11.5 | 5.8 |
| 70 m | 35.2 | 34.9 | 33.6 | 31.2 | 27.8 | 23.4 | 18.3 | 12.6 | 6.4 |
Si $v_0 = 292$ fps (soit -2.5%)
| $R_F/\theta_F$ | $0^\circ$ | $10^\circ$ | $20^\circ$ | $30^\circ$ | $40^\circ$ | $50^\circ$ | $60^\circ$ | $70^\circ$ | $80^\circ$ |
| Valeurs absolues | |||||||||
| 10 m | 6.1 | 6.1 | 5.8 | 5.3 | 4.7 | 4.0 | 3.1 | 2.1 | 1.1 |
| Valeurs relatives | |||||||||
| 15 m | 3.1 | 3.0 | 2.9 | 2.7 | 2.4 | 2.0 | 1.6 | 1.1 | 0.5 |
| 20 m | 6.1 | 6.1 | 5.8 | 5.4 | 4.8 | 4.0 | 3.1 | 2.1 | 1.1 |
| 25 m | 9.2 | 9.1 | 8.7 | 8.1 | 7.2 | 6.0 | 4.7 | 3.2 | 1.6 |
| 30 m | 12.3 | 12.2 | 11.6 | 10.8 | 9.6 | 8.0 | 6.3 | 4.3 | 2.2 |
| 35 m | 15.4 | 15.2 | 14.6 | 13.5 | 12.0 | 10.1 | 7.9 | 5.4 | 2.7 |
| 40 m | 18.4 | 18.3 | 17.5 | 16.2 | 14.4 | 12.1 | 9.5 | 6.5 | 3.3 |
| 45 m | 21.5 | 21.3 | 20.4 | 18.9 | 16.8 | 14.2 | 11.1 | 7.6 | 3.9 |
| 50 m | 24.6 | 24.4 | 23.4 | 21.7 | 19.3 | 16.2 | 12.7 | 8.7 | 4.4 |
| 55 m | 27.6 | 27.4 | 26.3 | 24.4 | 21.7 | 18.3 | 14.3 | 9.8 | 5.0 |
| 60 m | 30.7 | 30.5 | 29.3 | 27.2 | 24.2 | 20.4 | 15.9 | 10.9 | 5.6 |
| 65 m | 33.8 | 33.5 | 32.3 | 29.9 | 26.7 | 22.5 | 17.6 | 12.1 | 6.1 |
| 70 m | 36.9 | 36.6 | 35.2 | 32.7 | 29.1 | 24.6 | 19.2 | 13.2 | 6.7 |
ou si $v_0 = 307$ fps (soit +2.5%)
| $R_F/\theta_F$ | $0^\circ$ | $10^\circ$ | $20^\circ$ | $30^\circ$ | $40^\circ$ | $50^\circ$ | $60^\circ$ | $70^\circ$ | $80^\circ$ |
| Valeurs absolues | |||||||||
| 10 m | 5.6 | 5.5 | 5.3 | 4.8 | 4.3 | 3.6 | 2.8 | 1.9 | 1.0 |
| Valeurs relatives | |||||||||
| 15 m | 2.8 | 2.8 | 2.6 | 2.4 | 2.2 | 1.8 | 1.4 | 1.0 | 0.5 |
| 20 m | 5.6 | 5.5 | 5.3 | 4.9 | 4.3 | 3.6 | 2.8 | 1.9 | 1.0 |
| 25 m | 8.4 | 8.3 | 7.9 | 7.3 | 6.5 | 5.5 | 4.3 | 2.9 | 1.5 |
| 30 m | 11.2 | 11.0 | 10.6 | 9.8 | 8.7 | 7.3 | 5.7 | 3.9 | 2.0 |
| 35 m | 14.0 | 13.8 | 13.2 | 12.2 | 10.9 | 9.1 | 7.1 | 4.9 | 2.5 |
| 40 m | 16.7 | 16.6 | 15.9 | 14.7 | 13.1 | 11.0 | 8.6 | 5.9 | 3.0 |
| 45 m | 19.5 | 19.3 | 18.6 | 17.2 | 15.3 | 12.9 | 10.0 | 6.9 | 3.5 |
| 50 m | 22.3 | 22.1 | 21.2 | 19.7 | 17.5 | 14.7 | 11.5 | 7.9 | 4.0 |
| 55 m | 25.1 | 24.9 | 23.9 | 22.2 | 19.7 | 16.6 | 13.0 | 8.9 | 4.5 |
| 60 m | 27.9 | 27.7 | 26.6 | 24.6 | 21.9 | 18.5 | 14.4 | 9.9 | 5.0 |
| 65 m | 30.7 | 30.5 | 29.3 | 27.1 | 24.2 | 20.4 | 15.9 | 10.9 | 5.6 |
| 70 m | 33.5 | 33.2 | 32.0 | 29.7 | 26.4 | 22.3 | 17.4 | 11.9 | 6.1 |
Si l’archer tire sur une cible en devers, c’est-à-dire $\theta_F < 0$, l’expression approchée de $\alpha_0$ (7) indique que la correction est au premier ordre en $(v_0^{lim}/v_0)^2$ identique au cas symétrique $\theta_F>0$ et que les différences apparaissent seulement par le biais du second ordre via la fonction impaire $\sin \theta_F$ qui change de signe quand $\theta_F \leftrightarrow -\theta_F$. Visuellement, on peut se rendre compte de l’égalité des solutions $\alpha_0(\theta_F)\leftrightarrow \alpha_0(-\theta_F)$ sur la figure suivante où sont présentées les trajectoires de flèches à $\theta_F = 0^\circ, \pm 30^\circ et \pm 60^\circ$.
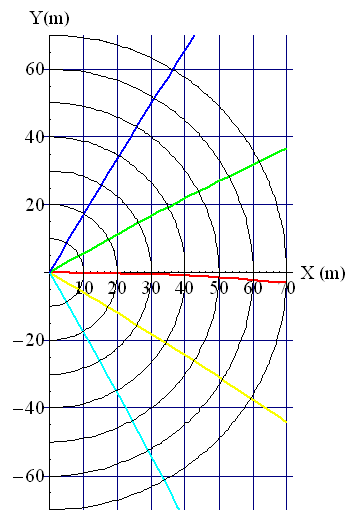
Numériquement à $v_0 = 300$ fps nous obtenons quasiment les mêmes valeurs que précédemment, soit
| $R_F/\theta_F$ | $0^\circ$ | $10^\circ$ | $20^\circ$ | $30^\circ$ | $40^\circ$ | $50^\circ$ | $60^\circ$ | $70^\circ$ | $80^\circ$ |
| Valeurs absolues | |||||||||
| 10 m | 5.9 | 5.8 | 5.5 | 5.1 | 4.5 | 3.8 | 2.9 | 2.0 | 1.0 |
| Valeurs relatives | |||||||||
| 15 m | 2.9 | 2.9 | 2.7 | 2.5 | 2.2 | 1.9 | 1.4 | 1.0 | 0.5 |
| 20 m | 5.9 | 5.8 | 5.5 | 5.0 | 4.4 | 3.7 | 2.9 | 2.0 | 1.0 |
| 25 m | 8.8 | 8.6 | 8.2 | 7.5 | 6.7 | 5.6 | 4.3 | 3.0 | 1.5 |
| 30 m | 11.7 | 11.5 | 10.9 | 10.0 | 8.9 | 7.4 | 5.7 | 3.9 | 2.0 |
| 35 m | 14.7 | 14.4 | 13.7 | 12.5 | 11.0 | 9.2 | 7.2 | 4.9 | 2.5 |
| 40 m | 17.6 | 17.2 | 16.4 | 15.0 | 13.2 | 11.1 | 8.6 | 5.9 | 3.0 |
| 45 m | 20.5 | 20.1 | 19.1 | 17.5 | 15.4 | 12.9 | 10.0 | 6.8 | 3.5 |
| 50 m | 23.5 | 23.0 | 21.8 | 20.0 | 17.6 | 14.7 | 11.4 | 7.8 | 3.9 |
| 55 m | 26.4 | 25.8 | 24.5 | 22.4 | 19.7 | 16.5 | 12.8 | 8.7 | 4.4 |
| 60 m | 29.3 | 28.7 | 27.2 | 24.9 | 21.9 | 18.3 | 14.1 | 9.6 | 4.9 |
| 65 m | 32.3 | 31.5 | 29.9 | 27.3 | 24.0 | 20.0 | 15.5 | 10.6 | 5.4 |
| 70 m | 35.2 | 34.4 | 32.5 | 29.8 | 26.1 | 21.8 | 16.9 | 11.5 | 5.8 |
Résumé et perspective
Dans cet article, nous avons abordé des cas concrets de tir à l’horizontal et à angle (montant et devers), et les relations entre ces situations dans le cadre de la détermination de l’angle initial du vol de la flèche pour atteindre un objectif fixe. Le modèle de vol de la flèche utilisé jusque là a ignorer le milieu, c’est-à-dire l’air ! Nous aborderons l’introduction de cet ingrédient avant d’aborder le réglage du viseur qui sera plus parlant que la notion d’angle bien que celle-ci soit plus générale comme nous le verrons. Donc, à suivre…