Introduction
La vitesse d’une flèche est intéressante à connaître
à plusieurs chefs :
- en vue de se poser la question de la balistique de
la flèche qui fera l’objet d’au moins un autre article - pour connaître le temps (grosso-modo) à quitter l’arc et qui conditionne le maintient
de la position parfaite de la rampe de lancement (c’est vous !) - enfin c’est un élément de comparaison des arcs comme on peut le voir dans
l’article article 45, donc connaître la façon dont on calcule cet élément de comparaison permet
un regard critique sur les valeurs annoncées.
"Rien ne se créer tout se transforme"
Même si nous n’allons pas faire de la Chimie ici, la formule célèbre
[1] illustre un principe fondamental : la conservation de l’énergie.
Pour faire simple on peut résumer la phase d’armement et de décoche comme suit.
La force de traction sur la corde va agir (on dit "travailler") tout au long
de l’ouverture de l’arc. Durant cette phase la corde répercute cette traction sur les branches de l’arc qui stocke de l’énergie potentielle, enfin lors de la décoche cette énergie potentielle se transforme en énergie cinétique qui résulte du mouvement de la flèche (nb. il y a éventuellement pertes d’énergie dans les mouvements de frictions des
piéces mobiles).
"Le travail c’est la santé... »
Bilan des forces sur un Long Bow
Examinons le schéma ci-dessous de l’ouverture de l’arc à pleine allonge en mode statique :
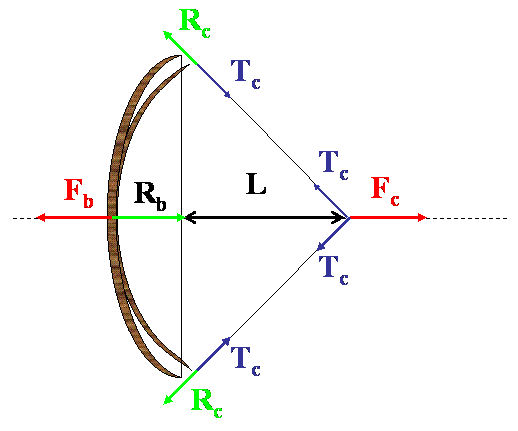
Il présente le bilan des forces en quatre points particulier : le point par lequel la corde est maintenue, les deux points symétriques d’accrochage de la corde aux branches de l’arc, enfin la poignée [2].
En chacun de ces points, le bilan des forces est nul, c’est-à-dire que la somme vectorielle des forces est nulle comme illustré sur le schéma ci-dessous :
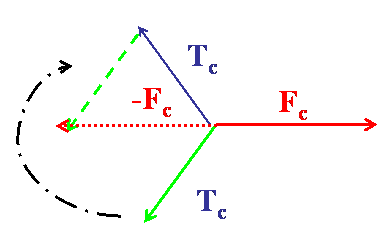
La force $F_c$ est égale en intensité et opposée en direction à la résultante des tensions $T_c$ sur les deux segments de la corde de part et d’autre du point de traction.
La tension de chaque segment de corde $T_c$ au niveau des branches et égale en intensité mais opposée en direction à la tension au niveau du point de traction car le bilan des forces exercées sur chaque segment doit être nulle sinon il y en résulterait un mouvement. En répétant le même schéma de raisonnement on trouve que la branche en réaction à cette traction engendre une force $R_c$ égale en intensité et opposée à la tension de la corde au point d’accrochage de la corde.
Enfin, l’arc étant maintenu au niveau de la poignée, il y a en ce point d’une part une réaction de la part de l’arc en réponse à la flexion des branches en imprimant une force égale est opposée à la somme des réactions des branches :
$R_b = -(R_c^{haut}+R_c^{bas})$. Cette réaction $R_b$ est exactement contrebalancée par la force du bras d’arc $F_b$ toujours parce que la poignée est au repos.
Ainsi on peut comprendre avec ce raisonnement qu’à chaque instant durant la phase d’armement non seulement il faut une force dans le bras d’arc égale est opposée à celle dans le bras de corde (cf. travail symétrique des muscles du dos…) mais également, l’énergie stockée dans les branches par leur flexion résulte d’une énergie due au déplacement de la force de traction $F_c$ le long de l’axe pointillé, de la position de repos de la corde à la position de pleine allonge.
Calcul du travail en général
Envisageons de calculer d’énergie de travail ou plus simplement le travail $W$ de la force $F_c$ que l’on notera dorénavant $F$ pour alléger la notation par la suite.
Tout d’abord, la force $F$ de l’archer s’exerce sur
un trajet rectiligne (en pointillé sur la figure img254) entre le point où la corde est au repos (Band ou
Brace Height) et le point où l’archer est à pleine allonge (Full Draw
Length). On note $L$ la longueur du trajet de traction.
D’une manière générale, on appelle travail élémentaire d’une force (noté
$dW$) le produit de l’intensité de cette force par la longueur du segment $dl$ sur lequel la force s’exerce :
$$ dW = F \times dl \quad \quad\quad\quad (1) $$
$F$ a pour unité le Newton (noté N, voir l’article
Unités US et Internationales pour des correspondances), tandis que les longueurs sont en
mètre (m). Une force de 1 N est environ celle qu’exerce une masselotte de 100 grammes accrochée au bout d’un fil à plomb suspendu au bout des doigts [3]. Le travail est donc en unité N.m qui dans le Système International est le Joule (J). Ainsi, une force de 1 N s’exerçant sur 1 m donne un travail de 1 J.
Si la force n’est pas constante au cours du déplacement $L$ alors on procède par addition des petits travaux $dW_i$ sur des petits segments $dl_i$ où la force prend une valeur quasi-constante $F_i$, et donc le travail total est le résultat :
$$ W = \sum_{i} dW_i = \sum_i F_i dl_i \quad\quad \mathrm{avec} \quad\quad \sum_{i} dl_i = L \quad \quad\quad\quad (2) $$
Quand on fait tendre les petits segments vers une longueur nulle
(par exemple en découpant le segment L en n petits segments de longueur L/n et en prenant des valeurs de n de plus en plus grande) alors on remplace les sommes discrètes ci-dessus par ce qu’on appelle une intégrale.
$$ W = \int_0^L F(l) dl \quad \quad\quad\quad (3) $$
Bigre que sa quo ! Il y a une représentation géométrique toute simple de cette expression mathématique qui de prime abord peut en faire pâlir plus d’un, voir même fuir ! Voilà de quoi il s’agit, en reprenant la formule (1), si on prend un rectangle de largeur $dl$ et de longueur $F$ alors $dW$ représente la surface de ce rectangle élémentaire. Prenons alors le graphe ci-dessous :
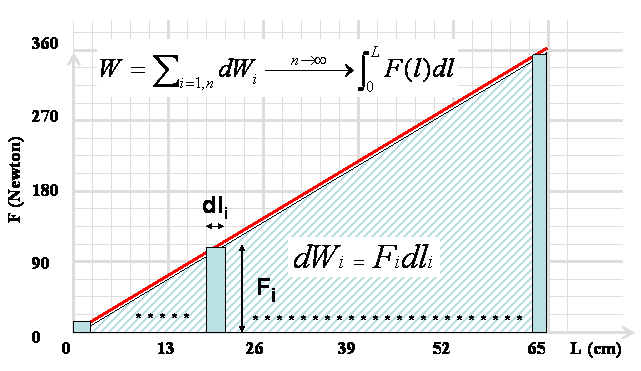
La valeur de la force $F(l)$ pour un allongement $l$ compris entre O et $L$ est reportée sur un graphe avec $F(l)$ verticalement (ordonnée) et $l$ horizontalement (abscisse). L’ensemble des mesures compose une courbe (au sens large car ici il s’agit d’une droite) rouge . On découpe l’axe horizontal en n rectangles élémentaires de longueur $dl_i = L/n$ et la hauteur de chaque rectangle est égale à la valeur de $F(l)$ pour l’allongement $l$ considéré (par exemple le rectangle considéré est situé à une allonge de 20 cm environ). La somme des surfaces des petits rectangles $\sum_{i} F_idl_i$ est une approximation de la [bleu clair]surface hachurée[/bleu clair] sous la courbe rouge d’autant meilleure
que la largeur des petits rectangles tend vers 0 (leur nombre quant à
eux tend vers l’infini).
Ainsi, l’intégrale (3) n’est rien d’autre que la surface comprise
entre l’axe horizontal et la courbe rouge .
Pour obtenir la courbe rouge pour un arc donné (long bow, recurve ou poulies), on peut procéder simplement à l’aide d’une flèche graduée et d’un peson. Pour une série d’allongements, on reporte la valeur de la force dans un graphe comme celui Représentation graphique d’une intégrale. Voyons dans les sections suivantes les différents cas de figures.
Arc long bow
Dans le cas d’un arc Long Bow les branches réagissent à la flexion comme un ressort. Un ressort exerce une force résistant à sa déformation et proportionnelle à son allongement, comme le montre le schéma suivant :
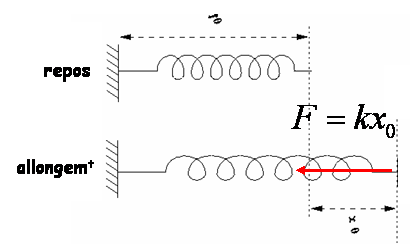
Cette force de réaction est notée $R_c$ dans la figure
Bilan des forces sur un arc Long Bow, or le bilan des forces nous incite à penser que $R_c = T_c = F_c/2$ donc finalement la force de traction de l’archer est proportionnel à l’allongement ce qui se traduit par
$$ F_c(l) = k \times l $$
avec k le coefficient de raideur équivalente de l’arc
et un graphe force-allongement (ou puissance-allongement cf. Unités US et Internationales) comme celui-ci

Le travail de l’archer quand il ouvre l’arc à pleine allonge est représenté par la surface hachurée qui n’est autre que celle d’un triangle de largeur $L$ et de hauteur la valeur maximale de la force $F_{max}$, ainsi
$$ \boxed{ W_{LB} = \frac{1}{2} F_{max} L } \quad \quad\quad\quad (4) $$
et la valeur du coefficient de raideur prend la valeur simple
$$ k = \frac{F_{max}}{L} \quad \quad\quad\quad (5) $$
Par exemple pour un arc de puissance de 60lbs avec une allonge de 25’’ (attention la valeur du band est soustrait, sinon cela ferait 7’’ de plus typiquement), on obtient un travail de :
$$ W = \frac{1}{2} \left[ 60 \times 4.45 \right] \left[25 \times 2.54 \times 0.01\right] \approx 85 \mathrm{N.m} = 85 \mathrm{J} $$
et $k = 420 N/m$.
A titre de comparaison, l’énergie de 100 Joules correspond à l’énergie électrique qu’il faut fournir pour faire fonctionner une ampoule de 100 Watt durant 1 seconde… Je vous laisse apprécier la comparaison de l’énergie fournie lors d’une séance d’entraînement de tir en salle, entre celle dépensée pour s’éclairer et l’autre pour bander les arcs. Pour ce qui concerne le coefficient de raideur, celui d’un peson est typiquement de 1800 N/m.
Un petit retour en arrière, quand on rapproche les deux résultats (4) et (5), en se souvenant de la formule (3), on a montré en passant que
$$ \int_0^L k x dx =\frac{k}{2} L^2 $$
valable quelque soit $k$ et en particulier lorsque $k=1$. D’une manière générale on montre que
$$ \int_0^L x^{n-1} dx = \frac{1}{n} L^n $$
dont découle la formule précédente quand $n=1$.
Vous me direz pourquoi tout ça ? C’est simple, l’approximation d’une force de réaction des branches qui ne dépend de l’allongement que linéairement (cf. de forme
$F (l) = k \times l$ ) est certainement une approximation bonne pour les petits allongements mais peut être de plus en plus fausse au fur et à mesure que les allongements deviennent importants. Ainsi, la valeur de $k$ peut dépendre elle-même de l’allongement et donc dans ce cas on généralise l’expression de la force de traction selon : $F(l) = k(l)\times l$ avec par exemple $k(l)=k_0+k^{’}_0\times l$. Ainsi $F (l) = k_0 \times l + k^{’}_0\times l^2$ et donc le travail devient :
$$ W = \int_0^L \left[ k_0 \times l + k^{’}_0\times l^2 \right] dl = k_0 \frac{1}{2} L^2 + k^{’}_0 \frac{1}{3} L^3 $$
Pour être plus concret et quantitatif, il faudrait disposer d’une courbe réelle Force/puissance-allongement pour un Long Bow.
Arc Recurve
Dans le cas d’un arc recurve, la différence majeure est bien la double courbure des branches qui permet de pouvoir disposer d’une plus grande énergie stockée comme on peut le voir sur le schéma ci-dessous.
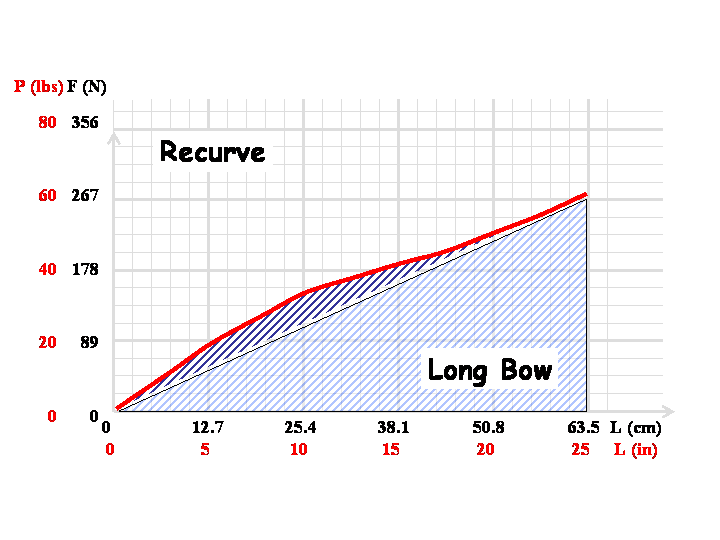
La courbe présente une plus grande pente correspondant à un plus grand coefficient de raideur, et le résultat net par rapport à un arc long bow en terme d’énergie (travail de traction) est la zone hachurée en [bleu marine] bleu marine [/bleu marine]. Par contre, la force que doit tenir l’archer à plein allonge de 60 lbs dans le cas de figure ici sera la même pour les deux arcs. La seule donnée de la puissance à la pleine allonge n’est donc pas une donnée suffisante pour comparer deux arcs.
Arc à poulies (Compound)
Le constat que la seule donnée de la puissance à pleine allonge n’est pas suffisante pour comparer deux arcs est d’autant plus criant lorsqu’il s’agit d’arcs à poulies ou à Cam.
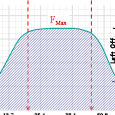
La courbe puissance/force-allongement typique est présentée sur le schéma suivant (merci à un anonyme pour avoir précisé la "vallée" et le "peak") :
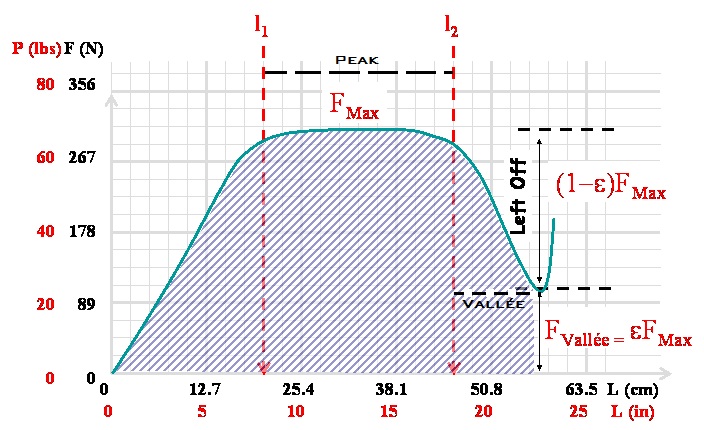
Il y a essentiellement 4 phases :
- une phase où la force se comporte comme pour un Long Bow/Recurve pour un allongement inférieure à $l=l_1$
- une phase où la force est quasi constante dans un intervalle d’allongement compris entre $l=l_1$ et $ l=l_2$
- une phase qui peut paraître paradoxale où la force diminue avec l’allongement de $l=l_1$ jusqu’à pleine allonge $l=L$
- une phase où la force augmente brutalement avec pour conséquence qu’il est quasiment impossible d’accroître l’allongement, cette phase est généralement dénommée le « mur ».
Ces 4 phases correspondent aux différentes positions des poulies excentrées.
On peut modéliser les 3 premières parties de la courbe qui servent pour le calcul du travail de la force de traction selon :
$$ F(l) = F_{Max} \left( \frac{l}{l_1} \right) \quad\quad\quad\quad 0 \leq l \leq l_1 $$
$$ F(l) = F_{Max} \quad\quad\quad\quad l_1 \leq l \leq l_2 $$
$$ F(l) = \epsilon F_{Max} \left( \frac{l-l_2}{L-l_2} \right)+ F_{Max} \left( \frac{l-L}{l_2-L} \right) \quad\quad\quad\quad l_2 \leq l \leq L $$
avec $F_{Max}$ la valeur maximale de la force de traction à exercer (cf. puissance de l’arc) et $\epsilon F_{Max}$ la valeur de la force réduite à pleine allonge (on nomme dans le jargon le let off la valeur de $1-\epsilon$).
L’intégrale qui représente la surface de la zone hachurée sous la courbe bleu a pour expression :
$$ \boxed{ W_{CO} = \int_0^L F(l) dl = \frac{1}{2} l_1 F_{Max} + (l_2-l_1) F_{Max} + \frac{1}{2} (L-l_2) (1+\epsilon) F_{Max} } \quad\quad\quad\quad (6) $$
Par exemple prenons les valeurs numériques du graphe Courbe de puissance pour un Compound :
- $ F_{Max} = 70$ lbs soit 311.5 N ;
- un let off de 64% soit $\epsilon=36\%$ ;
- $l_1=7,5$ inches, $l_2=17,5$ inches et $L=22$ inches soit 19 cm, 44.5 cm 55.9 cm respectivement (rappel : il faut rajouter le Band pour avoir le Draw Height total qui serait de l’ordre de 29 inches)
alors $W = 133$ J. Il y a un net accroissement de l’énergie emmagasinée à même force de traction maximale (ou puissance maximale par abus de langage) et allonge égales entre un arc à poulies et un arc long bow (et recurve).
Entre deux arcs à poulies de puissance maximale et allonge égales, il y a également une possible différence d’énergie emmagasinée due aux différentes formes des poulies (généralement appelées « Cam »). Cela se traduit en premier lieu par la largeur du « plateau » autour de la valeur maximale de la puissance avec en conséquence une plus grande raideur au départ (cf. on attaque le plateau plus tôt) et un front descendant plus raide également (cf. après le plateau la force chute brutalement).
La transformation !
L’énergie cinétique
Jusqu’à présent, nous avons essentiellement fait un raisonnement statique, c’est-à-dire qu’à chaque instant l’ensemble archer-arc-flèche est immobile, sauf grand vent !
Maintenant, lâchons tout… Heu, non ! Décochons en douceur et légèreté, voilà c’est mieux, ouf !
L’équilibre au point d’encoche est rompu et la somme des tensions des deux morceaux de corde sur l’image Bilan des forces sur un arc Long Bow imprime au moment de la décoche une force de propulsion horizontale égale en intensité à la force de traction à pleine allonge.
Donc, cette force donne à la flèche une dynamique de mouvement qui se traduit par un changement de vitesse. A chaque instant t durant un court intervalle de temps $dt$, un principe fondamental de la mécanique classique stipule que l’on a :
$$ F_{prop}(t) = \frac{p(t+dt) - p(t)}{dt} = \frac{m v(t+dt) - m v(t)}{dt} \quad\quad\quad\quad (7) $$
avec $v(t)$ la vitesse de la flèche à l’instant t, et $p= m v$ est ce que l’on appelle la quantité de mouvement de la flèche. Si on voulait faire un bilan complet des forces, il faudrait tenir compte du poids de la flèche, de la réaction de soutient et de frottement au niveau du décocheur, des déformations internes de la flèches (elle plie car elle est souple et que la pointe fait obstacle au mouvement)… Ceci dit la force de propulsion domine largement au niveau d’approximation où l’on se place pour calculer un ordre de grandeur de la vitesse d’éjection de la flèche et son temps de sortie de l’arc. Une remarque enfin, la masse m de la flèche entre en jeu dans la relation (7), car celle-ci est une application plus générale d’une loi de la mécanique classique laquelle s’applique également pour des systèmes balistiques qui perdent de la masse pour se mouvoir : ex. une fusée…
Durant $dt$, la flèche parcourt un chemin élémentaire de longueur
$dl = v(t) dt$ et la force $F_{prop}(t)$ produit un travail élémentaire égale à
$$ dW_{prop} = F_{prop} v(t) dt $$
En injectant la relation (7), il vient donc
$$ dW_{prop} = \left( \frac{m v(t+dt) - m v(t)}{dt} \right) v(t) dt = m v(t) \left[ v(t+dt) - v(t) \right] $$
L’expression entre […] représente un petit incrément de la vitesse durant l’intervalle de temps $[t,t+dt]$ qui se note $dv$ par analogie au petit incrément de temps $dt$ [4]. Ainsi, nous obtenons une expression du travail élémentaire de propulsion égale à
$$ dW_{prop} = m v dv $$
Par analogie avec la discussion lors de l’analyse de l’arc Long Bow (cf. $k \leftrightarrow m$ et $l \leftrightarrow v$), il est clair que le travail total de propulsion sera la somme des travaux élémentaires, ce qui nous l’avons vu se traduit par intégrale quand on considère des éléments de temps (de déplacement, de vitesse…) de plus en plus petits et finalement :
$$ W_{prop} = \int_{v(t=0)}^{v(t=t_{max})} m v dv = \frac{1}{2} m v^2_{F} \quad \quad \quad \quad (8) $$
où nous avons fait l’hypothèse que la vitesse (initiale) est nulle au moment de la décoche (cf. $ v(t=0)=0$)
et qu’au moment où la flèche quitte l’arc à $t=t_{max}$ la vitesse prend la valeur $ v_{F}$ (F pour Finale).
La notion de travail de propulsion est plus générale : c’est l’énergie cinétique de la flèche que l’on note par la suite $E_c$, avec pour valeur finale :
$$ \boxed{ E_c = \frac{1}{2} m v^2_F } \quad \quad\quad\quad (9) $$
L’énergie totale
Si on reprend le fil des événements, l’archer exerce un travail de traction, lequel est stocké sous forme d’énergie (potentielle) dans les branches de l’arc lequel restitue cette énergie lors de la décoche sous forme d’énergie cinétique de la flèche. Ainsi, on peut écrire la relation de conservation de l’énergie totale, somme d’énergie de stockage ou potentielle ($E_p$) et d’énergie de mouvement ou cinétique ($E_c$) du système arc-flèche
$$ \left( E_p + E_c \right)_{initial} = \left( E_p + E_c \right)_{final} $$
qui reflète une égalité entre deux plateaux d’une balance (vituelle) :
- le plateau de gauche est l’état initial du système juste avant la décoche : or rien ne bouge à ce moment là donc $E_c$ = 0, et l’énergie potentielle est égale au travail $W$ de la force de traction ;
- le plateau de droite est l’état final du système quand la flèche quitte l’arc : idéalement, il n’y a plus d’énergie stockée et toute l’énergie est contenue dans le mouvement de la flèche. Cette restitution ou transfert n’est pas parfait, il y a des frottements ici ou là, il y a des vibrations… On appelle rendement de l’arc le rapport entre l’énergie potentielle des branches et l’énergie cinétique de la flèche. Les bons arcs ont des rendements supérieurs à 90%. On négligera ces pertes d’efficacité par soucis de simplicité par la suite.
Donc finalement, nous pouvons écrire une relation donnant accès à la valeur de la vitesse d’éjection :
$$ W = \frac{1}{2} m v^2_F \quad \Rightarrow \quad \boxed{ v_F = \sqrt{\frac{2 W}{m}} } \quad\quad\quad\quad (10) $$
Vitesse en chiffres
La masse de la flèche intervient dans l’expression (10). A l’aide du logiciel Easton Shaft Selector (cf. Logiciels de choix de configurations arc-flèche et Easton Shaft Selector), il est aisé de calculer la masse de ses flèches si l’on ne dispose pas d’une balance de précision. D’un autre coté, deux masses conventionnelles existent dans la littérature d’archerie (cf. C’est quoi la Cam, je jargon des poulies ???) se référant aux notions de vitesse AMO ou IBO. Elles servent de benchmark pour comparer les arcs à poulies : 350 grains (= 22,7g, cf. Unités US et Internationales) pour la vitesse IBO, et 540 grains (= 35,0g) pour la vitesse AMO. Nous prendrons ces deux masses pour référence dans la suite.
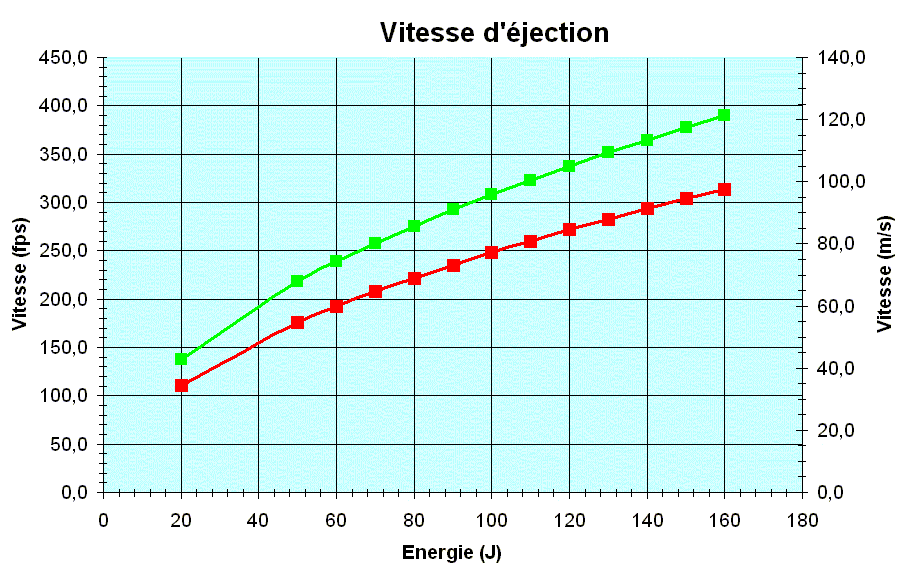
La table suivante donne pour différentes valeurs de l’énergie (cinétique) les valeurs en m/s et fps (feet per second) de la vitesse pour les deux masses de référence :
| W (J) | v (m/s) IBO | v(fps) IBO | v (m/s) AMO | v (fps) AMO |
|---|---|---|---|---|
| 20 | 42,0 | 137,8 | 33,8 | 110,9 |
| 50 | 66,4 | 217,9 | 53,5 | 175,4 |
| 60 | 72,7 | 238,6 | 58,6 | 192,1 |
| 70 | 78,6 | 257,8 | 63,3 | 207,5 |
| 80 | 84,0 | 275,6 | 67,6 | 221,9 |
| 90 | 89,1 | 292,3 | 71,7 | 235,3 |
| 100 | 93,9 | 308,1 | 75,6 | 248,0 |
| 110 | 98,5 | 323,1 | 79,3 | 260,1 |
| 120 | 102,9 | 337,5 | 82,8 | 271,7 |
| 130 | 107,1 | 351,3 | 86,2 | 282,8 |
| 140 | 111,1 | 364,5 | 89,5 | 293,5 |
| 150 | 115,0 | 377,3 | 92,6 | 303,8 |
| 160 | 118,8 | 389,7 | 95,6 | 313,7 |
Le graphique ci-dessous n’est que la traduction visuelle de la table.
Une première remarque s’impose : il est très important quand on compare des arcs en regardant les valeurs de vitesse affichées de se poser la question de quoi parle-t’on : IBO ou AMO ? A énergie fixée, la correspondance est donnée par simplement :
$$ v_{IBO} = \sqrt{\frac{540}{350}} \times v_{AMO} = 1,24 \times v_{AMO} $$
En d’autres termes, il y a une différence de 24% en faveur de la vitesse IBO ! Or, 24% est typiquement la différence entre passer d’une énergie de 100 J à 150 J, soit 50% sur la puissance de l’arc, une paille quoi… Noter également que la vitesse AMO est celle utilisée par le Easton Shaft Selector.
La seconde remarque tient de la comparaison entre des arcs Long Bow, Recurve et les arcs à Poulies/Cam : 94 m/s (310 fps) pour les premiers avec 70 livres (100 J) à pleine à allonge de 30’’ (rappel : Band de 7’’ + allongement de la corde), tandis que l’on obtient 107 m/s (350 fps), soit un gain de vitesse de 13%. Certes ce gain se fait avec un plateau à 70 livres qui donnent 130 J d’énergie, mais la puissance à pleine allonge n’est que d’environ 25 livres !
La troisième remarque que l’on peut faire est qu’à part des chasseurs qui privilégient le pouvoir de pénétration, les archers en compétition sont limités à une puissance de 60 livres. Il y a un facteur d’échelle simple pour tous les types d’arc (en première approximation) étant donné que les formules (4) et (6) montrent une loi de proportionnalité :
$$ W(60 \mathrm{lbs}) = \frac{6}{7} \times W(70 \mathrm{lbs}) \quad \Rightarrow \quad v(60 \mathrm{lbs}) = \sqrt{\frac{6}{7}} \times v(70 \mathrm{lbs}) = 0.86 \times v(70 \mathrm{lbs}) $$
Ainsi, on constate une réduction de 14% de la vitesse lors d’un passage de 70 lbs à 60 lbs. Ce type de relation d’échelle peut se faire pour tout couple de valeurs de puissance. Voici en application, une table pour les arcs à poulies selon la formule (6) :
| Puissance pic (lbs) | $W_{CO}$ (J) | vitesse IBO (fps) | vitesse AMO (fps) |
| 35 | 66,5 | 251,2 | 202,3 |
| 40 | 76,0 | 268,6 | 216,2 |
| 45 | 85,5 | 284,9 | 229,3 |
| 50 | 95,0 | 300,3 | 241,7 |
| 55 | 104,5 | 315,0 | 253,5 |
| 60 | 114,0 | 329,0 | 264,8 |
| 65 | 123,5 | 342,4 | 275,6 |
| 70 | 133,0 | 355,3 | 286,0 |
La figure traduit cette table en graphique
Avant de clore cet section sur la vitesse, deux commentaires :
- à titre de comparaison les flèches à 350 fps (100m/s) peuvent être aussi rapides que des petits plombs de 4,5mm tiré à l’air comprimé, mais sinon les balles de tireur à l’arme à feu sont plus rapides (200 à 1000 m/s)
- si nous revenons à nos flèches pacifistes et en inspectant la relation (7), on remarque que le rapport de la force de propulsion sur la masse de la flèche, n’est autre que l’accélération qu’elle subit instantanément (cf. le changement de vitesse sur un court instant). Or, on subit toutes et tous une accélération (sans le savoir). C’est l’attraction gravitationnelle qui est responsable de notre poids sur la balance : la valeur au niveau de la mer est de $ g = 9,81 \mathrm{m/s}^2$ (cf. Unités US et Internationales). Donc, on peut écrire :
$$ \mathrm{Acc\’el\’eration} = \frac{F_{prop}}{m} = k \times g \quad\Rightarrow \quad k = \frac{ F_{prop}}{m g} $$
Le paramètre $k$ n’est autre que le nombre de g que subit la flèche durant sa phase d’accélération (comme les pilotes d’avions ou les astro/cosmo/spatiau-nautes). A titre d’exemple même avec une puissance moyenne de 35 lbs, une flèche de 35O grains, subit
$$ k = \frac{35 \times 4,45}{22,7/1000 \times 9,81 } \approx 700 g $$
donc l’équivalent d’une force égale à 700 fois son poids !!! Il en résulte des déformations et c’est bien le moindre : d’où les flexions à symétrie axiale bien visible au ralenti comme sur les films disponibles sur le site de Beiter par exemple et que souvent on présente sous l’appellation le paradoxe de l’archer.
Le temps de propulsion
Le temps que met la flèche pour sortir de l’arc et prendre son envol a un impact sur la qualité de la stabilité de la rampe de lancement. On peut procéder d’abord à un calcul grossier qui donne un ordre de grandeur. Par exemple, pour un long bow à 60 lbs tiré sur 25’’, cela donne une vitesse finale de 86 m/s (284 fps) qui sur 76 cm (30 ‘’) donne un temps d’environ 9 ms (ms : millième de seconde).
On peut aller un peu plus loin pour affiner le résultat car on peut objecter que la vitesse maximale n’est atteinte qu’en fin de propulsion.
Prenons le cas d’un arc Long Bow (ou Recurve), l’équation du mouvement de la flèche est la solution de l’équation aux dérivées (équation différentielle) qui lient l’accélération à la force de propulsion par la l’équation (7) :
$$ m \dot{v}(t) \equiv m \frac{dv(t)}{dt} = F_{prop}(t) $$
Or, $v(t) = dx(t)/dt \equiv \dot{x}(t)$ (cf. variation instantanée de la position x(t) durant un intervalle de temps infinitésimal dt), et la dépendance temporelle de la force de propulsion est donnée par la position de la flèche x(t) via (cf. Courbe de puissance pour un Long Bow) :
$$ F_{prop}(t) = F_{prop}(L-x(t)) = F_{Max}\left( 1 - \frac{x(t)}{L} \right) \quad\quad\mathrm{pour}\quad\quad 0\leq x(t) \leq L $$
Ainsi, nous devons résoudre, c’est-à-dire donner l’expression de x(t), satisfaisant :
$$ m \ddot{x}(t) = F_{Max}\left( 1 - \frac{x(t)}{L} \right) $$
La résolution sort du cadre de cet article bien que les personnes intéressées pourront faire une analogie avec le mouvement d’une masselotte accrochée au bout d’un ressort. Il vient alors :
$$ x(t) = L \left[ 1 - \cos\left(\sqrt{\frac{F_{Max}}{m L}} \quad t \right)\right] $$
Bien entendu la flèche ne se met pas à osciller avec un mouvement de balancier avant-arrière car l’expression ci-dessus n’est valable que pour un temps compris entre 0 et $\pi/2 \times \sqrt{m L/F_{Max}}$. Ensuite, la flèche continue son chemin à vitesse constante pour sortir définitivement de la fenêtre d’arc.
Le graphique ci-dessous donne un exemple chiffré
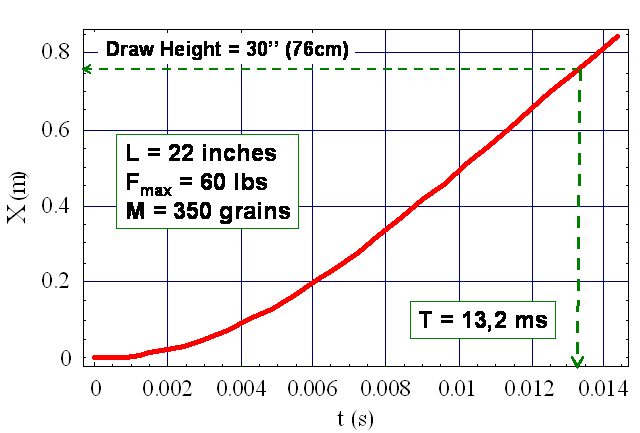
qui fourni la réponse plus précise : la flèche sort en un peu plus de 13 ms. La différence avec le calcul grossier est la prise en compte d’une sorte de retard à l’allumage matérialisé par la phase du début où l’établissement de la vitesse de croisière se fait sur quelque millisecondes.
Pour un arc à poulie, l’expression de la dépendance de la force de propulsion est moins simple (bien que simple par morceau) mais le raisonnement est le même que celui développé pour le long bow. Le résultat d’une application numérique est donné sur le graphe ci-dessous.
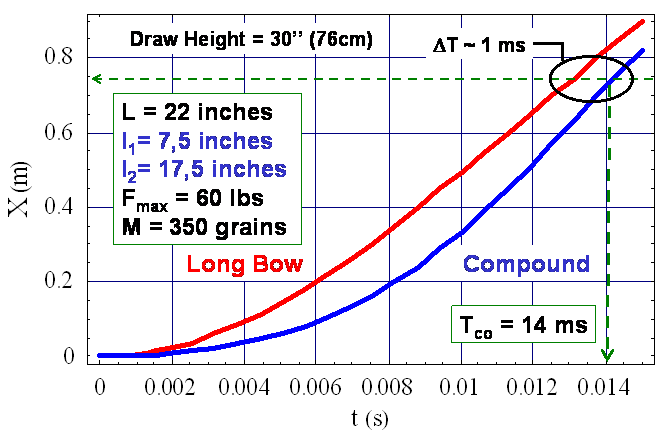
Ce résultat peut paraître surprenant car alors que la vitesse d’éjection d’un arc à poulie est plus grande qu’un long bow, il faut 1 ms de plus pour qu’une flèche quitte l’arc ! Or, en inspectant de prés la courbe d’évolution du déplacement de la flèche pour un arc à poulie, on se rend compte que la pente est plus raide après environ 10 ms. L’explication est simple : la vitesse instantanée de la flèche est justement la pente de cette courbe. La figure ci-dessous visualise la vitesse de la flèche au cours du temps pour les deux types d’arc.
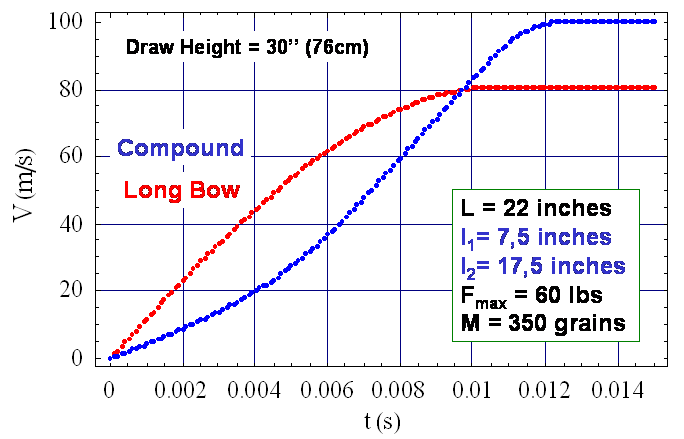
Ainsi, la vitesse d’éjection pour un arc à poulies est bien supérieure mais la vitesse instantanée n’est supérieure à celle d’un long bow que dans le dernier quart de la phase de propulsion.